INF2310 vår 2012 - Løsningshint 9

Oppgave 1 - Shannon-Fano-koding og Huffman-koding

1. Shannon-Fano-oppdelingene blir for denne modellen entydige for en gitt sortering av symbolene (for sortering av symbolene kan vi velge om "b" eller "c" skal plasseres som nest hyppigst). Dersom vi bruker den sorteringen av symbolene som er angitt i modellen og følger forslaget på s. 37 i forelesningsnotatet om å etter hver oppdeling tilordne 0 til venstre gruppe og 1 til høyre gruppe, får vi følgende tre:
   
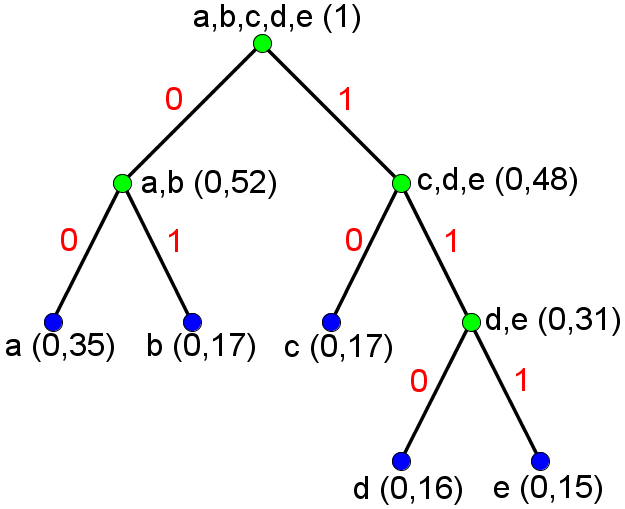
   Dette gir følgende kodebok:
   

   Symbol	a	b	c	d	e
   Shannon-Fano-kodeord	00	01	10	110	111

   Gjennomsnittlig antall biter per symbol etter Shannon-Fano-koding (når vi koder et ord som har identisk normalisert histogram som den angitte modellen) er gitt som summen av punktproduktet av sannsynlighetene og lengden av Shannon-Fano-kodeordene, som blir 2,31.
2. Huffman-sammenslåingene blir for denne modellen entydige. Hvis vi følger forslaget på s. 42 i forelesningsnotatet om å etter hver sammenslåing tilordne 0 til den mest sannsynlige gruppen og 1 til den minst sannsynlige gruppen, og definerer at "b" skal bli tilordnet 0 når den slås sammen med "c", får vi følgende tre:
   
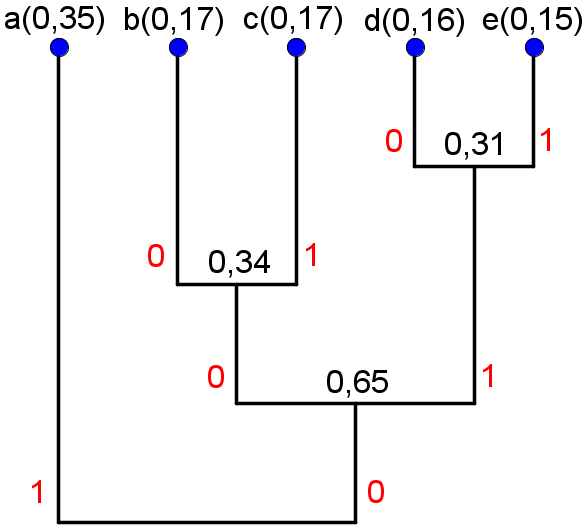
   Dette gir følgende kodebok:
   

   Symbol	a	b	c	d	e
   Huffman-kodeord	1	000	001	010	011

   Gjennomsnittlig antall biter per symbol etter Huffman-koding (når vi koder et ord som har identisk normalisert histogram som den angitte modellen) er gitt som summen av punktproduktet av sannsynlighetene og lengden av Huffman-kodeordene, som blir 2,3.
3. Symbol "a" får lengre kodeord i Shannon-Fano-kodeboken enn i Huffman-kodeboken. Siden gjennomsnittlig antall biter per symbol er lavere for Huffman-koden enn for Shannon-Fano-koden kan vi konkludere med at det må være plassbesparende å bruke det kortere kodeordet som Huffman-koden gjør - selv etter at man har tatt hensyn til at det medfører at andre symboler, her "b" og "c", får lengre kodeord.
4. Forslag til sannsynlighetsmodell:
   

   Symbol	a	b	c	d	e
   Sannsynlighet	0,42	0,15	0,15	0,14	0,14

   Ingen av algoritmene vil oppføre seg annerledes når de anvendes på denne modellen (forutsatt at vi bruker den angitte sorteringen av symbolene), noe som gjør at begge kodebøkene er fortsatt gyldige. Det gjennomsnittlig antall biter per symbol etter Shannon-Fano-koding (når vi koder et ord som har identisk normalisert histogram som den angitte modellen) blir nå 2,28, mens tilsvarende gjennomsnitt etter Huffman-koding blir 2,16.
   
   Bemerkning: Det kan virke som både Shannon-Fano-algoritmen og Huffman-algoritmen "takler" denne modellen bedre ettersom begge gjennomsnittene blir mindre for denne modellen enn den opprinnelige. "Takler" en modell er selvsagt et upresist begrep, men når man studerer kodingsalgoritmer som koder enkeltsymboler er det naturlig å vurdere hvor god en algoritme er ut fra hvor mye kodingsredundans den gjenlater etter koding, altså hvor stor differansen er mellom det gjennomsnittlige bitsforbruket per symbol etter koding og entropien. For den første modellen er entropien omtrent 2,23, og for den andre modellen er entropien omtrent 2,14. Dette vil si at kodingsredundansen øker for Shannon-Fano-algoritmen fra første modell til andre modell, mens reduseres for Huffman-algoritmen. Det virker derfor naturlig å si at Huffman-algoritmen takler den nye modellen bedre, mens Shannon-Fano-algoritmen takler denne nye modellen dårligere, og at grunnen for at begge gjennomsnittene blir mindre for den nye modellen er at denne modellene har mindre entropi og kan derfor (iallfall teoretisk sett) komprimeres kraftigere med kodingsalgoritmer som koder enkeltsymboler.

Oppgave 2 - Huffman-dekoding

Følg hintet og du skal ende opp med ordet "Digital bildebehandling".

Oppgave 3 - Huffman-koding uten kodingsredundans

En Huffman-kode av ordet "DIGITAL OVERALT!" er:

der "^" markerer mellomrom.

Vi har i alt 16 symboler, men bare 12 forskjellige, og antall forekomster er enten 2 ("A", "I", "L", "T") eller 1 ("^", "!", "D", "E", "G", "O", "R", "V"). Det betyr at alle de N=12 sannsynlighetene kan skrives som brøker der telleren er 1 og nevneren er en toerpotens (8 eller 16). Altså kan alle symbolsannsynlighetene uttrykkes som 1/2^k for forskjellige heltallige verdier av k. I dette tilfellet vet vi Huffman-koding vil gi ingen kodingsredundans, som betyr at entropien er lik det gjennomsnittlige antall biter per symbol etter Huffman-koding. Vi kan derfor finne entropien av dette ordet ved å beregne gjennomsnittlig antall biter per symbol etter Huffman-koding, noe som ikke innebærer noen logaritme-beregninger.

Når man utfører beregningene finner man at både entropien og det gjennomsnittlige antall biter per symbol etter Huffman-koding er 3,5:

R = (8*3 + 8*4) / 16 = 56 / 16 = 3,5

H = -4*(1/8)*log₂(1/8) - 8*(1/16)*log₂(1/16) = log₂(2³)/2 + log2(2⁴)/2 = 3/2 + 4/2 = 3,5

Oppgave 4 - Differansetransform og Huffman-koding

1. Histogrammet til gråtonebildets intensitetsverdier er h = [11 22 15 6], dvs. at h(0) = 11, h(1) = 22, h(2) = 15 og h(3) = 6. Fra dette histogrammet ser vi at Huffman-algoritmen vil:
   1. Slå sammen gruppen som består av 3 og gruppen som består av 0, som gir en ny gruppe med total forekomst på 17,
   2. Slå sammen gruppen som består av 2 og gruppen som består av 0 og 3, som gir en ny gruppe med total forekomst på 32,
   3. Slå sammen gruppen som består av 1 og gruppen som består av 0, 2 og 3.
   Totalt gjør dette at lengdene av Huffman-kodeordene blir 3, 1, 2 og 3 for henholdsvis intensitet 0, 1, 2 og 3, noe som gir et gjennomsnittlige antall biter per piksel etter Huffman-koding av dette bildet på omtrent 1,91.
2. Differansetransformen av bildet er:
   

   0	0	0	1	0	0	1	0	0
   0	0	1	0	-1	0	2	0	0
   1	-1	0	0	1	0	0	1	0
   1	-1	1	0	1	-1	1	1	0
   1	0	0	1	-1	0	0	2	0
   1	0	0	1	0	0	1	-1	1

3. Histogrammet til differansebildet er gitt ved h(-1) = 6, h(0) = 29, h(1) = 17 og h(2) = 2, som kan skrives som h = [6 29 17 2] under forståelse om at intervallet er heltallene mellom -1 og 2. Det er greit å innse at Huffman-algoritmen vil resultere i nøyaktig samme kodebok for dette histogrammet som for histogrammet til det opprinnelige gråtonebildets intensitetsverdier (se deloppgave 1), med unntak av at intensitetsverdiene som Huffman-kodeordene representerer nå er byttet ut med differanseverdier som har én lavere verdi. Dermed vil lengdene av Huffman-kodeordene være 3, 1, 2 og 3 for henholdsvis differansene -1, 0, 1 og 2, noe som gjør at vi vil bruke omtrent 1,61 biter per piksel i gjennomsnitt etter Huffman-koding av differansebildet.
4. Entropien av gråtonebildet gir en nedre grense for hvor kompakt gråtonebildet kan kodes dersom vi bare koder ett piksel av gangen. Videre vet vi at denne grensen bare oppnås når alle sannsynlighetene i det normaliserte histogrammet kan skrives som 1/2^k for (muligens forskjellige) heltallige k. Ettersom dette kravet ikke er oppfylt i det opprinnelige gråtonebildet, er det en nødvendighet at Huffman-kodingen resulterer i et gjennomsnittlig antall biter per piksel som er høyere enn entropien.
   
   Når vi bruker differansetransformen ser vi ikke bare på ett piksel av gangen. Å Huffman-kode differansebildet endrer ikke dette; i den totale kompresjonsprosedyren vil man (forsøke å) både redusere intersampel redundans (ved differansetransformen) og kodingsredundans (Huffman-kodingen). Entropien til det opprinnelige gråtonebildet gir ikke noen nedre grense for kompresjonsraten i dette tilfellet, og det er derfor mulig å oppnå høyere kompresjonsrater enn entropien tilsier (som vi gjør her).
   
   Bemerkning: Siden vi Huffman-koder differansebildet vil entropien av differansebildet gi oss en nedre grense for hvor mange biter per piksel vi i gjennomsnitt må bruke etter kodingen (som blir et mål på ikke-redundansen i differansebildet når vi kun enkeltvis ser på differanseverdiene). Denne entropien er omtrent 1,53, så vi ser at også her vil Huffman-kodingen resultere i lav kodingsredundans.

Oppgave 5 - Løpelengdetransform og Huffman-koding
... og "differansetransform" i tid

1. Histogrammet til gråtonebildets intensitetsverdier er h = [6 19 21 8], dvs. at h(0) = 6, h(1) = 19, h(2) = 21 og h(3) = 8. Fra dette histogrammet ser vi at Huffman-algoritmen vil:
   1. Slå sammen gruppen som består av 0 og gruppen som består av 3, som gir en ny gruppe med total forekomst på 14,
   2. Slå sammen gruppen som består av 0 og 3 og gruppen som består av 1, som gir en ny gruppe med total forekomst på 33,
   3. Slå sammen gruppen som består av 2 og gruppen som består av 0, 1 og 3.
   Totalt gjør dette at lengdene av Huffman-kodeordene blir 3, 2, 1 og 3 for henholdsvis intensitet 0, 1, 2 og 3, noe som gir et gjennomsnittlige antall biter per piksel etter Huffman-koding av dette bildet på omtrent 1,87.
2. Resultatet etter og utført løpelengdetransformen på hver rad blir:
   1. (0,2), (1,3), (2,4)
   2. (0,2), (1,4), (2,3)
   3. (1,2), (0,2), (1,2), (2,3)
   4. (1,2), (2,4), (3,3)
   5. (1,3), (2,4), (3,2)
   6. (1,3), (2,3), (3,3)
3. Histogrammet til tallparenes intensitetsverdier er h = [3 7 6 3], dvs. at h(0) = 3, h(1) = 7, h(2) = 6 og h(3) = 3. Fra dette histogrammet ser vi at Huffman-algoritmen vil:
   1. Slå sammen gruppen som består av 0 og gruppen som består av 3, som gir en ny gruppe med total forekomst på 6,
   2. Slå sammen gruppen som består av 0 og 3 og gruppen som består av 2, som gir en ny gruppe med total forekomst på 12,
   3. Slå sammen gruppen som består av 1 og gruppen som består av 0, 2 og 3.
   Totalt gjør dette at lengdene av Huffman-kodeordene blir 3, 1, 2 og 3 for henholdsvis intensitet 0, 1, 2 og 3, noe som gjør at Huffman-koden vil bruke 37 biter på å representere disse intensitetene.
   
   Histogrammet til tallparenes løpelengder er gitt ved h(2) = 7, h(3) = 8 og h(4) = 4, som kan skrives som h = [7 8 4] under forståelse om at intervallet er heltallene mellom 2 og 4. Det er rimelig enkelt å innse at Huffman-algoritmen vil først kombineres 4 og 2, for så å kombinere 3 med den forrige kombinasjonen. Dermed vil lengdene av Huffman-kodeordene blir 2, 1 og 2 for henholdsvis løpelengde 2, 3 og 4, noe som gjør at Huffman-koden vil bruke 30 biter på å representere disse løpelengdene.
   
   Siden det er 54 piksler i det opprinnelige bildet, vil det gjennomsnittlige antall biter per piksel etter denne kompresjonsprosedyren bli omtrent 1,24.
4. Differansebildet blir:
   

   0	0	-1	0	0	-1	0	0	0
   0	0	0	0	-1	-1	0	0	0
   0	-1	0	0	0	0	-1	0	0
   0	-1	-1	-1	0	-1	-1	0	0
   0	0	0	0	-1	-1	-1	0	0
   0	0	0	0	0	0	0	-1	0

   Dette bildet inneholder kun to forskjellige symboler, noe som gjør at vi både kan og må bruke 1 bit per piksel for å kode dette bildet dersom vi skal kode hvert symbol for seg selv.