INF2310 vår 2012 - Løsningshint 10

Oppgave 1 - Løpelengdetransform av binære bilder

1. Hvis vi har N løpelengder i en rad så kommer vi til å bruke nN biter for å representere dette med en n-biters naturlig binærkode, mens vi trenger 2ⁿ-1 biter for å representere raden uten kompresjon. For å oppnå plassreduksjon må løpelengderepresentasjonen ta mindre biter enn det ukomprimerte bildet, altså må nN < 2ⁿ-1, noe som vi kan omskrive til N < (2ⁿ-1)/n.
2. For n=4 får vi: N < (2⁴-1)/4 = 15/4 (= 3,75). Altså må antall løpelengder i raden være mindre eller lik 3 for å oppnå plassreduksjon når n=4. PS: Antall piksler i raden er da 2⁴-1 = 15, så middelverdien av løpelengdene må minst være 15/3 = 5 for at vi skal oppnå kompresjon.
   For n=8 får vi: N < (2⁸-1)/8 = 255/8 (= 31,875). Altså må antall løpelengder i raden være mindre eller 31 for å oppnå plassreduksjon når n=8. PS: Antall piksler i raden er da 2⁸-1 = 255, så middelverdien av løpelengdene må minst være 255/31, omtrent 8,2, for at vi skal oppnå kompresjon.
   For n=10 får vi: N < (2¹⁰-1)/10 = 1023/10 (= 102,3). Altså må antall løpelengder i raden være mindre eller 102 for å oppnå plassreduksjon når n=10. PS: Antall piksler i raden er da 2¹⁰-1 = 1023, så middelverdien av løpelengdene må minst være 1023/102, omtrent 10,0, for at vi skal oppnå kompresjon.
3. Forholdet mellom "bredden på bildet" og den øvre grensen til "det høyeste antall løpelengder vi kan ha og fortsatt oppnå kompresjon" er (2ⁿ-1) / ((2ⁿ-1)/n) = n.
   Dette forholdet angir en nedre grense for hva middelverdien av løpelengdene kan være og vi fortsatt oppnår kompresjon; middelverdien av løpelengdene må være ekte større enn n for at vi skal oppnå kompresjon.
   Kombinert med uttrykket fra deloppgave 1 har vi derfor at: For store bilder kan vi tillate oss å ha mange løpelengder (den øvre grensen for N er da stor), men likevel må hver løpelengde være større i gjennomsnitt enn for mindre bilder (n stiger, dog ganske langsomt sett i sammenheng med at den definerer bildets bredde ved 2ⁿ-1).

Oppgave 2 - Løpelengdetransform, differansetransform og Huffman-koding

1. Hver rad vil bestå av 8 løpelengder, og alle løpelengdene er lik 512/8 = 64. Ved bruk av 8-biters naturlig binærkoding av både intensitetsverdier og løpelengder vil vi totalt bruke 8 * (8*2 + 2) = 8*18 = 144 biter per rad.
2. Bildet inneholder 512 like rader. Derfor vil Huffman-koden av en rad være den samme som Huffman-koden av hele bildet.
   
   Etter løpelengdetransform kan hver rad skrives som: 0 64 32 64 64 64 96 64 128 64 160 64 192 64 224 64 0 0. Vi kan bruke disse hyppighetene til å finne et Huffman-kodetre:
   
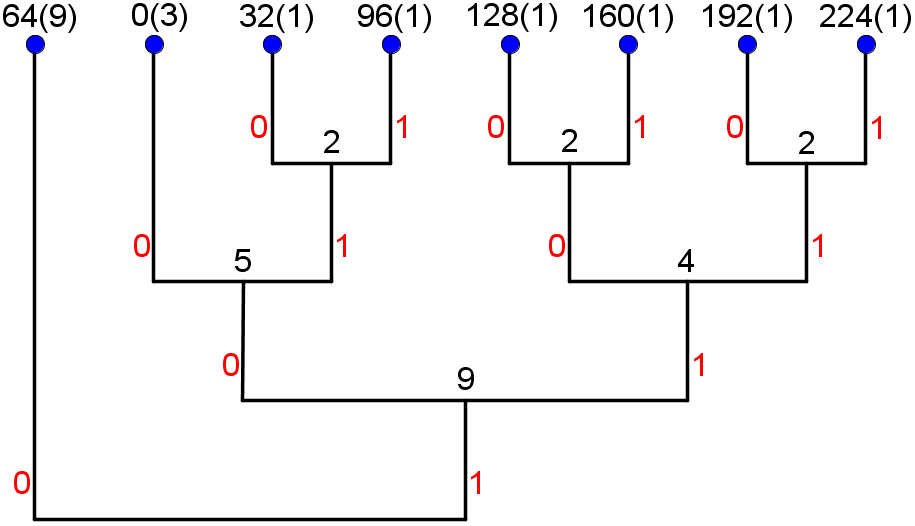
   Dette gir oss følgende Huffman-kodebok:
   

   Symbol	0	32	64	96	128	160	192	224
   Huffman-kodeord	100	1010	0	1011	1100	1101	1110	1111
   Antall forekomster	3	1	9	1	1	1	1	1

3. Fra tabellen over ser vi kodeordet og antall forekomster av hvert symbol for hver rad. Multipliserer vi hver kodeordlengde med de tilsvarende hyppighetene får vi det totale antall biter som blir brukt til å representere løpelengdetransformen og EOL-merket; 1*9 + 3*3 + 6*(4*1) = 9+9+24 = 42 biter per rad. Siden det er 512 piksler per rad i det opprinnelige bildet, tilsvarer dette et gjennomsnittlig bitforbruk per piksel på 42/512 = 21/256, som er omtrent 0,08. Ettersom vi bruker 8 biter per piksel i det ukomprimerte bildet, får vi en omtrentlig kompresjonsrate på 8/0,08 = 100 (eksakt regning hadde gitt omtrent 97,5). Siden alle radene er like vil både bitforbruket og kompresjonsraten gjelde for hver rad såvel som for hele bildet.
   
   Hvis det hadde blitt bedt om å beregne det gjennomsnittlige antall biter per løpelengdekoeffisient (altså, per ene verdi av løpelengdeparene), inklusivt EOL-merket, ville svaret vært 42/18 = 7/3, som er omtrent 2,33.
4. I det opprinnelige bildet er det åtte forskjellige gråtoner og alle er like sannsynlige. Dette gjør at enhver 3-biters binærkode som tilordner kodeord til de åtte forskjellige gråtonene er en optimal kode når vi koder enkeltpiksler. Kompresjonsraten blir da 8/3.
   
   (Vi kunne i stedet argumentert med at entropien til dette bildet er eksakt 3; 8*(-(1/8)log₂(1/8)) = 8*3/8 = 3, og videre at dette optimumet opplagt kan oppnås i dette tilfellet, nettopp ved en 3-biters binærkode.)
   
   I det differansetransformerte bildet vil vi for hver rad finne sju elementer lik 32 (ved overgangen mellom ”trappetrinnene”), mens ellers bare 0 (i alt 505 elementer). Ettersom det bare finnes to verdier i bildet, vi ett bit per piksel være det beste vi i praksis kan oppnå når vi bare koder enkeltdifferanser. Vi får dermed en kompresjonsrate på 8/1= 8. Altså får vi 3 ganger høyere kompresjonsrate etter differansetransformen enn originalt, dersom vi i begge tilfeller koder enkeltsymboler på en best mulig måte.

Oppgave 3 - Lempel-Ziv-Welch-koding

1. Fra det oppgitte histogrammet ser vi at én gyldig fremgangsmåte for Huffman-algoritmen er:
   1. Slå sammen gruppen som består av "b" og gruppen som består av "c", som gir en ny gruppe med total forekomst på 15,
   2. Slå sammen gruppen som består av "a" og gruppen som består av "d", som gir en ny gruppe med total forekomst på 21,
   3. Slå sammen gruppen som består av "a" og "d" og gruppen som består av "b" og "c".
   I den resulterende Huffman-kodingen vil alle kodeordene ha lengde 2. Siden Huffman-koding er optimal under begrensningen at vi koder enkeltsymboler, så betyr dette at alle kodinger der alle kodeordene har lengde 2 er optimale på samme måte som Huffman-koden. Naturlig binærkoding er én slik koding.
2. Følg oppskriften for senderen og du vil ende opp med følgende LZW-kodesekvens: 0 1 4 2 6 3 8 0 10 9 12 7 14.
3. Kodesekvensen fra deloppgave 2 inneholder 13 koder, og med naturlig binærkoding bruker vi 4 biter på å representere hver av dem. Totalt vil vi derfor bruke 4*13 = 52 biter på det første ordet. Siden dette ordet inneholder 36 symboler, tilsvarer dette et gjennomsnittlig bitforbruk per symbol (av det opprinnelige ordet) på 52/36 = 13/9, som er omtrent 1,44.
4. Entropien er en nedre grense for hvor mange biter vi trenger per symbol når vi koder symbolene enkeltvis. LZW-koding koder derimot ikke symbolene enkeltvis. Dermed er ikke LZW-koding begrenset av entropien slik som Shannon-Fano-koding og Huffman-koding er.
   
   (Vi kunne alternativt argumentert med at LZW-koding prøver å redusere både intersampel redundans og kodingsredundans, og at entropien kun er knyttet til kodingsredundansen.)
5. Følg oppskriften for senderen og du vil ende opp med følgende LZW-kodesekvens: 0 1 1 2 3 1 4 0 2 11 3 0 0 14 15 2 7 4 7 14 8 18 7 1.
6. Kodesekvensen fra deloppgave 2 inneholder 24 koder, og med naturlig binærkoding bruker vi 5 biter på å representere hver av dem. Totalt vil vi derfor bruke 5*24 = 120 biter på det andre ordet. Siden dette ordet inneholder 36 symboler, tilsvarer dette et gjennomsnittlig bitforbruk per symbol (av det opprinnelige ordet) på 120/36 = 10/3, som er omtrent 3,33.
7. LZW-koding premierer mønstre i meldingen. Et nødvendig kriterium for at LZW-koding skal resultere i plassreduksjon er derfor at det finnes mønstre i meldingen som kodes. Det vil det normalt ikke gjøre i en melding som består av symboler som er plassert på tilfeldige posisjoner i meldingen, som i det andre ordet i denne oppgaven.

Oppgave 4 - Aritmetisk koding

1. Symbolene "a", "b", "c" og "d" har forekomster på henholdsvis 2, 1, 2 og 5. Én gyldig fremgangsmåte for Huffman-algoritmen er derfor:
   1. Slå sammen gruppen som består av "a" og gruppen som består av "b", som gir en ny gruppe med total forekomst på 3,
   2. Slå sammen gruppen som består av "a" og "b" og gruppen som består av "c", som gir en ny gruppe med total forekomst på 5,
   3. Slå sammen gruppen som består av "a", "b" og "c" og "d" og gruppen som består av "d".
   I den resulterende Huffman-kodeboken vil lengdene av Huffman-kodeordene bli 3, 3, 2 og 1 for henholdsvis symbol "a", "b", "c" og "d", noe som gjør at gjennomsnittlige antall biter per piksel etter Huffman-koding på 1,8.
2. Begynn med [0,1) som "current interval" og beregn nytt "current interval" for hvert symbol (bruk f.eks. formlene på s. 15 i forelesningsnotatet). Det siste "current interval" som du beregner, som vil være det intervallet du velger for EOD-symbolet, skal være omtrent [0.11483761, 0.11483778).
   
   For å finne den kortest mulige binære representasjonen av et tall i dette intervallet, kan vi omgjøre de (eksakte) grensene av det siste "current interval" til sine binære representasjoner (se f.eks. s. 20 i forelesningsnotatet), samtidig som vi leter etter den første posisjon der disse representasjonene avviker (som vi f.eks. gjorde på s. 22 i forelesningsnotatet). Den binære sekvensen av disse like sifrene etterfulgt av 1 vil normalt* være en tall i intervallet, og vil isåfall også være den kortest mulige binære representasjonen av et tall i dette intervallet.
   
   For våre grenser får vi de binære sekvensene 000111010110010... og 000111010110011... for henholdsvis nedre og øvre grense, og siden 0,000111010110011₂ < 0,114837783₁₀ så er dette et tall i intervallet vårt (siden den binære representasjonen av den nedre grensen starter med 0,000111010110010, så er 0,000111010110011₂ nødt til å være større enn denne grensen). (Ved å regne ut den veiede summen av de negative toerpotensene (se f.eks. s. 19 i forelesningsnotatet), får vi at 0,000111010110011₂ = 0,11483765₁₀.) Den kortest mulige binære representasjonen av et tall i intervallet vårt er altså 0,000111010110011₂, så den aritmetiske koden for hele ordet er 000111010110011.
   
   * Den binære sekvensen av de like sifrene etterfulgt av 1 kan være nøyaktig lik den øvre grensen. Dette er svært usannsynlig, men hvis det er tilfellet, vil ikke denne sekvensen etterfulgt av 1 være et tall i intervallet vårt (husk at nedre grenser er inkludert (fra og med), mens øvre grense ikke er inkludert (til, men ikke med)). I dette tilfellet kan vi være nødt til å bruke noen ekstra biter på å ende opp med et tall som er i intervallet vårt.
3. Siden det er 15 biter i den aritmetiske koden og 10 symboler i ordet, vil vi i gjennomsnitt bruke 1,5 biter per symbol etter den aritmetiske kodingen.
4. Ettersom aritmetisk koding koder flere symboler som ett flyttall, vil dens bitforbruk ikke være begrenset av entropien, ettersom sistnevnte kun er optimumet når vi koder enkeltsymboler. Å kode flere symboler som ett tall gjør også at vi potensielt kan redusere redundans mellom symbolene, altså intersampel redundans.
   Ettersom modellen vår kun baserer seg på symbolforekomster, kan vi ikke si at aritmetisk koding av denne typen prøver å redusere intersampel redundans - vi må betrakte denne reduksjonen som en tilfeldighet. (Reduksjon av intersampel redundans kan derimot betraktes som et av hovedpoengene ved å benytte en høyereordens modell eller en adaptiv modell, og for slike aritmetiske kodinger vil vi naturligvis potensielt kunne oppnå langt bedre kompresjonsrater.)