Partiklene i boksen vi skal simulere for gassmekanikken i motoren må være uniform fordelt og ha en gaussisk hastighetsfordeling. Det løser vi ved å gi de tilfeldige verdier som følger nettopp disse prinsippene. De begrenses ved å simulere elastisk støt med veggen og hullet i bunnen defineres på samme måte. Men det går jo ikke an å beregne en motor som ikke beveger seg i tid. For det bruker vi en metode som kalles Euler-Cromer, den oppdaterer posisjon og hastigheter for hvert tidssteg.
Vi trenger også å sjekke at trykket holder seg konstant for at vi kan anta at akselerasjonen til boksen er konstant, som nevnt i tidligere blogginnlegg. Dette gjør vi ved å sjekke formelen mot beregningene som datamaskinen gjør og ser hvor mye forskjell det er i prosent.
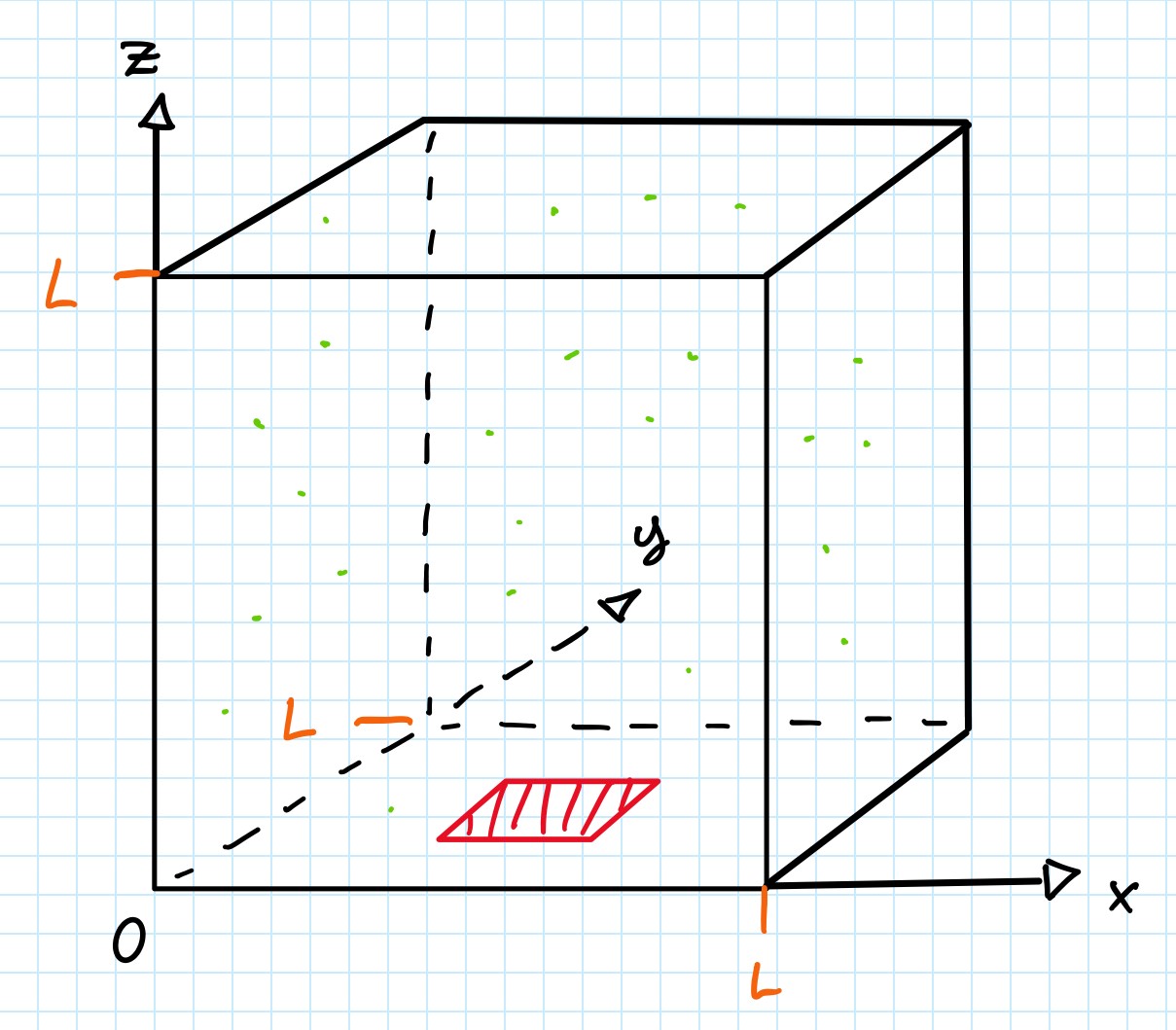
Vi starter med å definere den bittelille boksen vår på papir, som vist i figur 1. Her tegner vi den opp i alle tre dimensjonene og definerer lengden på den, som er 1 \(\mu m\) [mikrometer, \(10^{-6}\) m]. Arealet av en vegg vil være \(10^{-12}\) [\(m^{2}\)] og volumet av hele boksen er \(10^{-18}\) [\(m^3\)]. Nå som den er ferdig, lager vi tilfeldige posisjoner til alle partiklene som skal være i den med en funksjon som heter "numpy.random.uniform". Denne kaster terning for både x-, y- og z-posisjonene, men terningen har bare sider som tilsammen tilsvarer en uniform fordeling. Men partiklene vil stå helt i ro om vi ikke gir de en liten dytt.
Du kan se for deg at du har fått enorme krefter og verden står plutselig stille. Du ser noen som sitter på en huske helt i ro og bestemmer deg for å dytte på dem, hva skjer? Ingenting selvfølgelig, tiden står jo stille. Men, med engang tiden begynner å gå vil energien du ga plutselig gi fart på husken og personen detter ned og slår seg. Du får litt dårlig samvittighet, men du gjorde det for vitenskapen. Det samme gjør vi med partiklene, vi gir dem en start fart i alle dimensjoner som er fordelt gaussisk med funksjonen "numpy.random.normal". Denne er også tilfeldig, men denne terningen har kun sider som tilsvarer gaussisk fordeling! Og som vi husker så har den gaussiske fordelingen til hastigheter en midlere verdi \(\mu = 0\) og et standardavvik på \(\sigma = \sqrt{\frac{kT}{m_H}}\).
Da er vi vel ferdige? Neida! Partiklene må jo få lov til å bevege seg! Husk at vi skal med denne simuleringen, telle antall partikler som forlater boksen og lagre hastigheten de har før det. Det er faktisk ganske enkelt og du har sikkert allerede funnet det ut selv! Vi har jo hastighet allerede og posisjonen de står i, så da er det jo så enkelt at vi bare bruker det at \(strekning = hastighet \cdot tid\). Vi setter systemet i gang ved å bruke Euler-Cromer metoden. Nei, det er ikke et ukjent romvesen eller ditt største mareritt! Det er en metode som legger avstanden partikkelen har reist over en viss tid (\(v\Delta t\)) til den posisjonen den allerede har (\(x_0\)). Vi liker ikke formler her i skogen, men hvis Euler-Cromer skulle hatt en, ja da ville den sett slik ut:
\(x_1 = x_0 + v\Delta t\)
Hvor \(x_1\) er den nye posisjonen til partikkelen. Hvordan får vi flyttet de enda en gang da, spørr du. Vel, vi setter formelen inn i en "løkke" som opererer akkurat som en mor. Du spørr mor, hvor skal jeg nå? Mor peker dit. Du spørr igjen, hva med nå da? Mor peker til en annen plass. Du er partikkelen, mor er formelen og hver gang du spørr så har det gått en hvis tid (\(\Delta t\)).
