Sidan vi her ikkje har med ekstremt høge eller låge temperaturar å gjere, kan vi forenkle og gjere ei tilnærming av gassen. Men vent, blir det ikkje veldig varmt i tuten til raketten? Jau, det blir det, men her er det prat om berre 3000 kelvin (forhåpentlegvis) som er slik passe høg temperatur i kosmisk skala, og ein ideell temperatur for forbrenning av hydrogen.
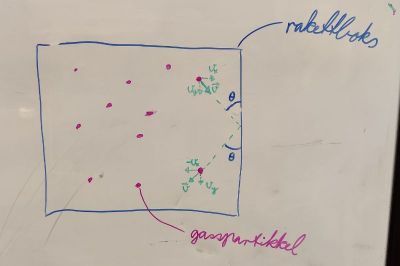
Vi forventar òg at det er inga interaksjon mellom gasspartiklane, dei kolliderar ikkje med kvarandre, og vi forventar at ein kollisjon med veggen er elastisk som betyr at den kinetiske energien er bevart og kun endrar forteiknet til hastigheitskomponenten som står normalt på veggen. Partiklane er heller ikkje utstrekte, men berre punktpartiklar. Dette gjev oss ein ideell gass.
Og når vi nå fyrst snakkar om ideelle gassar så kjem vi ikkje utanom tilstandslikninga:
\(P = nkT\)
der P er trykk, n er antaltettleik (altså antal partiklar per volum), k er Boltzmann konstanten og T er temperaturen. Dette er ei likning som trekkjer ein relasjon mellom trykket og tettleiken til ein gass. Utleiinga av denne formelen er litt tidkrevjande dersom ein ikkje har gjort det før (sjølvsagt), og det krevs ein stø hjerne og gode algebrakunnskapar, men for den ivrige lesaren har vi lagt til utleiinga i eit vedlegg her.
Og når vi no pratar om trykket til gassen er vi òg nøydd til å nemne korleis vi reknar ut dette trykket. Trykk er kraft per areal, ikkje sant? Og denne krafta som blir utført på arealet kan vi skrive som \(\frac{dp}{dt}\), den tidsderiverte av rørslemengda der \(p = |\vec{p}| \). Tilnærmar vi den får vi \(\frac{\Delta p}{\Delta t} = \frac{2p_x}{\Delta t}\). Men kvar i reine verd kom det to-talet frå?! Den totale endringa i rørslemengd er \(2p_x\), som er den vi er ute etter. Set vi dette inn i likninga for trykk får vi \(P_x = \frac{F}{A} = \frac{2mv_x}{\Delta t A}\). Merk at vi her pratar om ein kollisjon med ein vegg i x-retning som døme.
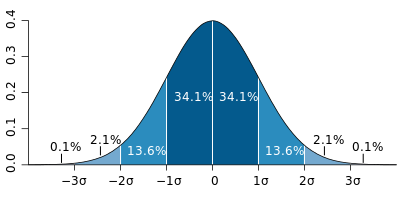
Fordi vi forventar ein ideell gass kan vi bruke gaussisk sannsynsfordeling av partiklane. Ei tilfeldig gaussisk fordeling der altså. Med gaussisk meiner vi uniform. Denne normalfordelinga, som det òg blir kalla, er særs viktig i matematikken, det heng saman med noko som heiter sentralgrenseteoremet. Dette skal vi ikkje gå så mykje inn på her, men det innebær at eit tilfeldig utval av noko, uavhengig av korleis fordelinga av dette "noko" var i utgongspunktet, vil vere normalfordelt slik som kurva på figuren her.
 Skriv inn bildetekst her...
Skriv inn bildetekst her...
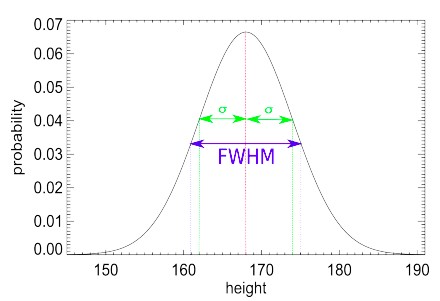
"Dette var då ein fin graf" tenkjer du sikkert no. Jau, det har du heilt rett i, og her er kvifor! Som vi kan sjå på denne andre figuren til høgre her, så ser vi no noko som liknar på Hufsa. Augane hennar, den greske bokstaven sigma \(\sigma \), er standardavviket, som seier noko om kor langt frå gjennomsnittsverdien enkelte verdiar i gjennomsnitt ligg. Gjennomsnitt meg her og gjennomsnitt meg der, kva så med FWHM? Det står for Full Width at Half Maximum, som seier noko om bredden på kurva ved halve maksimumsgjennomsnittet (den raude streken), som ofte vert kalla \(\mu\). Les vi av FWHM, finn vi \(\sigma\) ved
\(\sigma = \frac{FWHM}{\sqrt{8 \ln2}}\)
Det som er veldig interessant her, og ikkje minst veldig snodig, er at ved normalfordeling, sjølv kva det handlar om, finn vi alltid ved \(\sigma\), \(2\sigma\) og \(3\sigma\) høvesvis desse fordelingane: 68%, 95% og 99.7%.
Maxwell-Boltzmann fordeling er noko vi kjem til å få veldig godt bruk for. Dette er ei sannsynsfordeling som vert brukt på rørslemengd, energi eller hastigheita til partiklane i ein ideell gass. Det er dette vi vil bruke for å gje partiklane ei initell hastigheit. Vi kjem nå sjølvsagt ikkje med ei sannsynsfordeling med fint namn utan å gje dykk ein formel! Ta ein titt på dette dyret:
\(\begin{align*} P(\vec{v}) &= \left(\frac{m}{2\pi kT}\right)^\frac{3}{2} e^{-\frac{1}{2}\frac{mv^2}{kT}} \end{align*}\)
der k er Boltzmanns konstant, m er partikkelmassa, T er temperaturen i kelvin og v er total hastigheit i alle retninga.
KJELDER
Figur 1: https://www.uio.no/studier/emner/matnat/astro/AST2000/h21/undervisningsmateriell/lecture_notes/part1a.pdf, http://www.caprino.no/shop/images/movie_dvd3/askeladden1.jpg, samt ei god dose Paint.
Figur 2: Eigen illustrasjon.
Figur 3: https://no.wikipedia.org/wiki/Normalfordeling#/media/Fil:Standard_deviation_diagram.svg
Figur 4: https://www.uio.no/studier/emner/matnat/astro/AST2000/h21/undervisningsmateriell/lecture_notes/part1a.pdf
