"Skal vi slippe ned kua nå?" spør Tuslingen ivrig. "Vent på simuleringen, Tuslingen. Den vil si om kua overlever eller ikke" beroligger Askeladden. "Vi har da alle simuleringene vi trenger om atmosfæren! Slipp den nå!" sa Tuslingen urolig. "Vi trenger først en modell for hvor stor kraft kua opplever gjennom det hele! Den skal jo overleve!" poengterer Askeladden og setter foten ned.
Askeladden tar blyanten sin fatt og begynner å regne. Kraften som kua og fallskjermen vil hovedsaklig oppleve er luftmotstand. Den har en formel som nevnt under:
\(F_d = \frac{1}{2}\rho(r) C_d A v_{drag}^2\), hvor \(\rho(r)\) er tettheten til atmosfæren, \(C_d\) er kalt luftmotstandkonstanten som forteller hvor motstandsdyktig overflaten til et objekt er for atmosfæren, \(A\) er arealet til objektet og \(v_{drag}\) er hastighetskomponenten med hensyn til romskipets- og atmosfærens hastigheter.
Askeladden vet allerede hva tettheten med hensyn på radius (\(\rho(r)\)) til planeten er, fra tidligere innlegg. Han antar at luftmotstands konstanten er \(C_d = 1\) basert på kuas størrelse og form. Arealet til objektet som han setter til å være fallskjermen vil være en ukjent som han må "gjette på", ved å sjekke motstanden for forskjellige arealer. Modellering av hastigheten til kua gjennom atmosfæren \(v_{drag}\) trenger en egen formel for å være korrekt.
Han definerer hastighetsvektoren til båten i forhold til planeten som \(\vec{v}\)og den kombinerte hastighetsvektoren til atmosfæren til Åtvekdal i forhold til planeten som \(\vec{w}\). Askeladden antar videre at atmosfæren er knyttet til rotasjonen av planeten, som betyr at den får samme angulær hastighet som Åtvekdal \(\omega_{å} = 2\pi / T_{å}\). \(T_å\) er perioden til Åtvekdal i sekund.
Ut i fra definisjonen av radiell enhetsvektor, som kan skrives som \(\frac{r}{|r|} = \left[\cos\theta, \sin\theta\right]\). I figur 2 så kan man enklere se hvordan man kan uttrykke radiell hastighetsvektor ved sinus og cosinus. Fra samme figur kan man se at tangensiell enhetsvektor er ortogonal med den radielle og Askeladden skriver dermed \(e_\theta = \left[-\sin\theta, \cos\theta\right]\) fra enkel trigonometri. Posisjonen til atmosfæren er avhengig av radius fra sentrum av planeten, angulærmomentet til planeten og tangensiell enhetsvektor for den beveger seg langs planeten. Askeladden kommer da fram til uttrykket under:
\(\vec{w}(r, \theta) = \frac{2\pi r}{T_å}\left[-\sin\theta, \cos\theta\right]\), hvor \(\theta\) er vinkelen mellom radiusen og x-aksen og \(r\) er avstanden fra sentrum av planeten til posisjonen i atmosfæren.
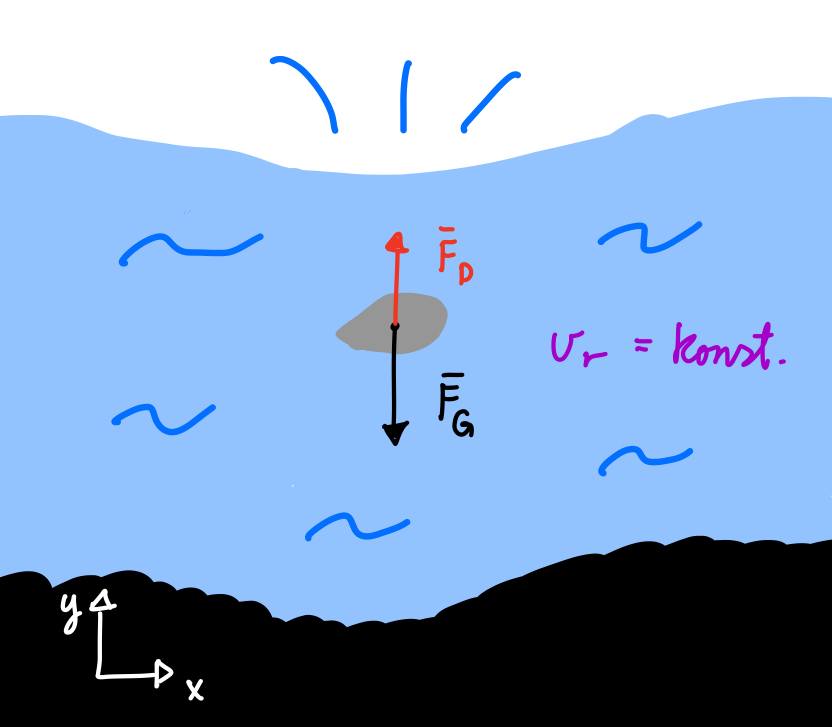
Tar man en sniktitt på figur 1 til Askeladden, kan man se at luftmotstanden virker i motsatt retning av hastigheten. Hastigheten som inngår i motstandsuttrykket er avhengig av hastigheten til atmosfæren og hastigheten til kua. Askeladden sette hastigheten til kua med respekt til planeten som positiv og kan dermed skrive at hastigheten i forhold til atmosfæren blir \(\vec{v}_{drag} = \vec{w}(r, \theta) - \vec{v}(r, \theta)\).
En annen hastighet som Askeladden er interessert i er et uttrykk for terminalhastigheten til kua. Terminalhastighet er et uttrykk for den høyeste hastigheten et objekt kan ha i en væske/gass. I en mer enklere forklaring er det en formel for å regne ut farten en stein har påvei mot bunnen av en innsjø.
For Askeladden er det ikke steinen som bekymrer han, men kua når den skal treffe bakken. Ved å finne terminalhastigheten, vil Askeladden vite hvilken hastighet kua kommer til å ha før den treffer bakken. Luftmotstand vil virke på kua med engang den treffer atmosfæren. Det betyr at Askeladden trenger å finne ut hvordan hastighetene, både tangensial- \(v_\theta\) og radiellhastighet \(v_r\) oppfører seg etter punktet hvor kua er innenfor atmosfæren. Oppdelingen av hastighetsvektoren kan skrives som formelen under:
\(\vec{v} = v_\theta\vec{e}_\theta + v_r\vec{e}_r\), hvor \(\vec{e}_\theta\) er tangensiell enhetsvektor og \(\vec{e}_r\) er radiell enhetsvektor.
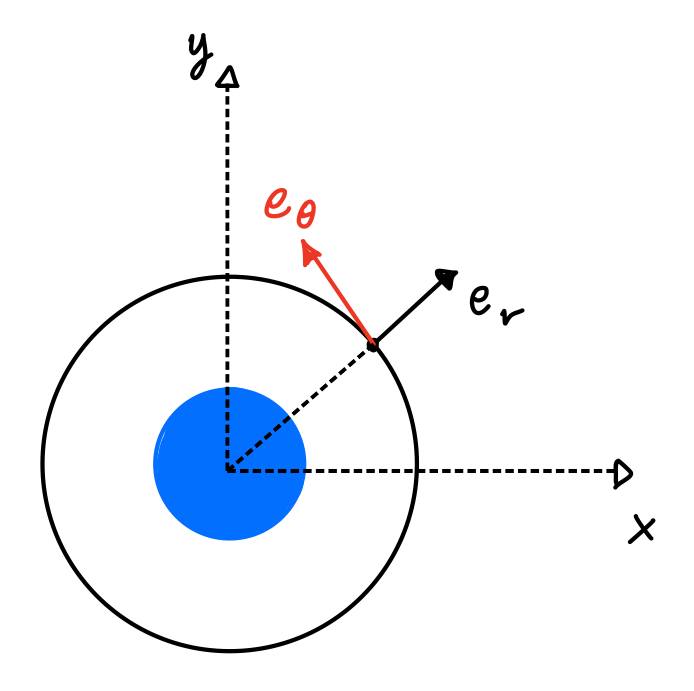
Enhetsvektorer kan være vanskelige å forstå, det var det for Askeladden også. Han tegnet geometrisk hva disse to enhetsvektorene betyr i figur 2.
I det kua blir sluppet fra båten og sakker ned, følger Askeladden med å ikke sakke farten for mye slik at kua faller rett ned. Ved å sende kua inn med en stor tangensial hastighet mot atmosfæren, vil den bruke lengre tid i en tynnere atmosfære for å sakke ned. Dette betyr igjen at man klarer å holde luftmotstanden under et kritisk punkt. Kua vil oppleve størst luftmotstand i tangensiellretning først, fordi den har størst tangensiell hastighet ved innganngen til atmosfæren. Dermed vil tangensialhastigheten \(v_\theta \rightarrow 0\) og kua vil ende opp med kun terminalhastighet. Atmosfæren vil sørge for at kua kun ender opp med planeten sin angulærhastighet.
Askeladden funderer og funderer med blyanten sin, gjør store bevegelser og snakker høyt og tydelig til seg selv. Tuslingen derimot sitter og tegner for seg selv alle de fine fjellene han kan se fra kanten på båten. Han har til og med tegnet en liten Tusling oppe på en av knausene til Åtvekdal.
Askeladden durer videre med å sette tangensialhastighet til null \((v_\theta = 0)\). Det han lurer på nemlig, er hva som vil være kua sin konstante terminale hastighet i radiell retning \(v_r\). Om han finner et uttrykk for dette, så kan han nemlig estimere fallskjermstørrelsen OG være sikker på at kua lander trygt! Han utleder et uttrykk for dette under:
\(\sum F = 0 \rightarrow F_G - F_d = 0\rightarrow F_G = F_d\), han starter med å definere kreftene som virker på kua i atmosfæren. Her er \(F_G = \frac{GMm}{r^2}\) gravitasjonskraften og \(F_d = \frac{1}{2}\rho(r)A v_r^2\) luftmotstandskraften. Askeladden setter disse lik hverandre og løser for radiell hastighet \(v_r\).
\(\frac{1}{2}\rho(r)Av_r^2 = \frac{GMm}{r^2}\rightarrow v_r(r) = \sqrt{\frac{2GMm}{\rho(r)Ar^2}}\rightarrow v_r(r_å) = \sqrt{\frac{2GMm}{\rho_0Ar_å^2}}\), den første løsningen for radiell hastighet er terminalhastighet hvor som helst i atmosfæren. Den andre løsningen er ved overflaten til Åtvekdal.
Askeladden kan fra terminalhastighets uttrykket over lett utlede en formel for arealet til fallskjermen ved å løse for \(A\). Fallskjermen kommer til å oppleve størst luftmotstand der det er høy tetthet, så Askeladden utleder en formel for arealet til fallskjermen ved overflaten til Åtvekdal under.
\(A = \frac{2GMm}{\rho_0 r_å^2 v_{r, safe}^2}\), hvor \(v_{r, safe} = 3\) [m/s] er hastigheten som kua kan ha før den treffer bakken uten å knekke beina.
Arealet til selve kua ser askeladden bort i fra, da arealet til fallskjermen trolig nok kommer til å være større enn arealet til selve kua. Det endelige arealet til fallskjermen derimot endte med å bli \(A = 113\) [\(m^2\)]. Dette kommer av at tettheten ved overflaten til Åtvekdal er relativt tynn, som gir lite luftmotstand. Større areal vil dermed kompensere ved å dekke større overflater med luft.
Askeladden reiser seg og ser på Tuslingen som dagdrømmer om is-fiske på Åtvekdal. "Nå har jeg dimensjonene Tuslingen! La oss ta fram symaskinen og begynne på fallskjermen!" roper Askeladden entusiastisk. Tuslingen skvetter til "Fangst! Nei, fantastisk! Den ligger under dekk, jeg går å henter den" sier han og tusler ned under dekk.
Askeladden lener seg over kanten på båten og skikker ned i det han tenker til seg selv: "Hva skjer rett før kua treffer bakken da?".
