Den dominerande gravitasjonskrafta
Anta at raketten er nærme ein av planetane. Kva er så avstanden mellom raketten og planeten dersom gravitasjonskrafta frå planeten i denne posisjonen er k gongar større enn gravitasjonskrafta frå stjerna? Det skal vi her kome fram til.
Gravitasjonskrafta frå planeten er altså k gongar større enn den frå stjerna. Her luktar det Newtons gravitasjonslov lang veg! La oss setja den opp og sjå kva vi finn
\(\begin{align*} \vec{F}_{g, p} &= k\vec{F}_{g, s} \\ G \frac{M_p m}{l^2} \hat{r} &= kG\frac{M_s m}{r^2}\hat{r} \end{align*}\)
Dette her er rett fram algebra, og det kan dykk banne på at dykk blir gode på i løpet av Fysikk 2 (dersom dykk har det). Det dykk kanskje ikkje har vore borti er nemninga \(\hat{r}\). Den er for å vise kva for ei retning krafta verkar i, og her verkar ho altså i r-retninga som vil seie radiell retning.
Her er \(m\) massa til raketten, \(M_p\) og \(M_s\) er høvesvis planet- og solmassa, \(r\) er \(|\vec{r}|\) som er avstanden frå sola til raketten, og \(l\) er avstanden frå planeten til raketten. Og \(G \) er som vanleg gravitasjonskonstanten.
Vi ser med ein gong at vi kan stryke \(m\), \(G\) og \(\hat{r}\). Det gjev oss
\(\frac{M_p}{l^2} = k \frac{M_s}{r^2}\)
som vi skal løyse med omsyn på \(l\):
\(\begin{align*} M_p &= l^2 k \frac{M_s}{r^2} \\ l^2 &= \frac{M_p r^2}{k M_s} \\ l &= r\sqrt{\frac{M_p}{k M_s}} \\ l &= |\vec{r}|\sqrt{\frac{M_p}{kM_s}} \qquad \blacksquare \end{align*}\)
Kor nærme må vi vere for å sjå?
Kor nærme må vi vere for å få teke eit bilete av destinasjonsplaneten? Eller for å seie det på ein anna måte: kor nærme må vi vere planeten for at vi skal kunne skimte det på eit bilete?
Det vert sagt at ein kan skimte objektet ein tek bilete av dersom det tek opp meir enn èin piksel. Vi antek:
- at kameraet har ein piksedimensjon på \(P \times P\) der \(P \) er pikslar
- at kameraet har eit synsfelt på \(F \times F\) der \(F\) er målt i gradar
- at planeten tek opp to pikslar på biletet og har ein radius \(R\)
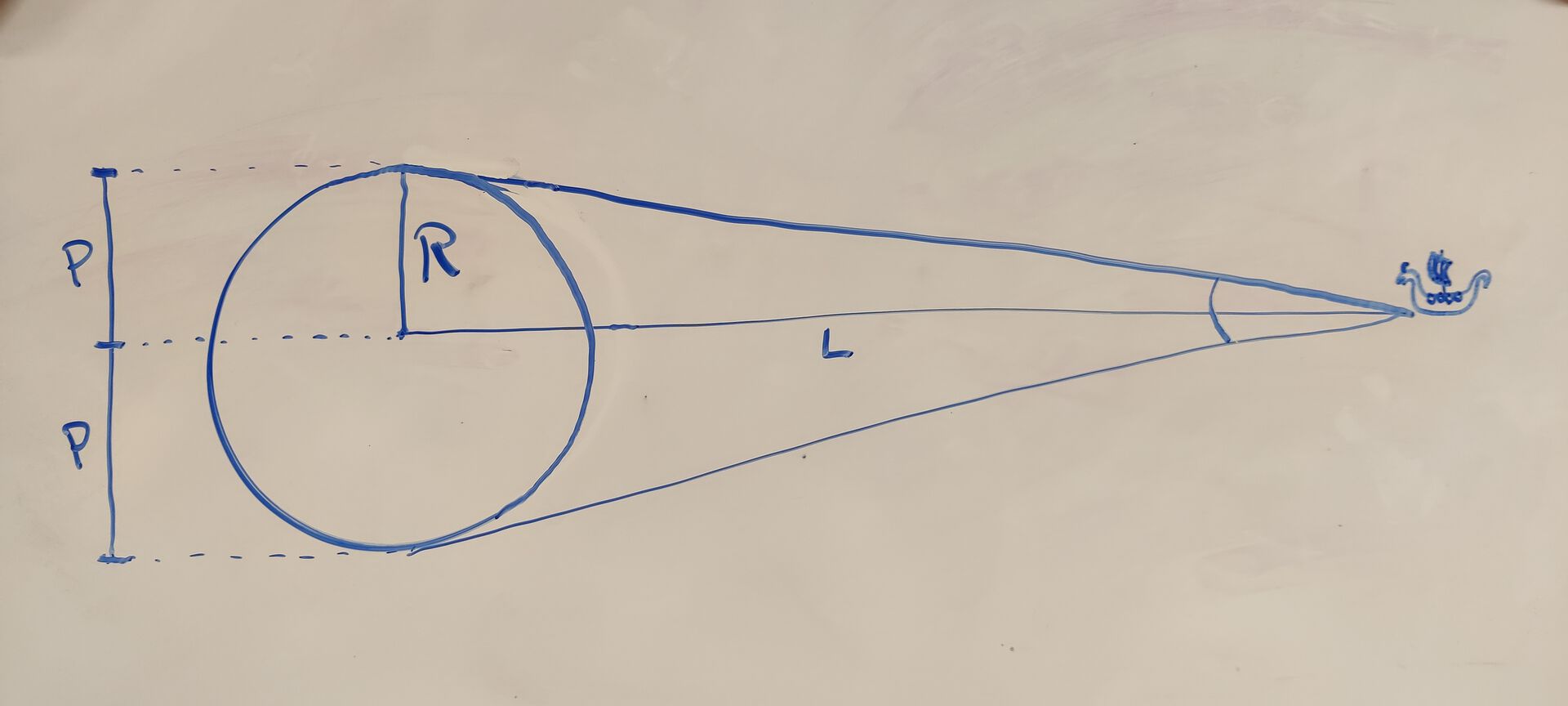
Vinkel per piksel kan då bli skriven som \(\frac{F}{P}\). Ved enkel trigonometri gjev dette oss at
\(\begin{align*} \tan{\frac{F}{P}} &= \frac{R}{L} \\ \frac{R}{L} &= \tan{\frac{F}{P}} \\ \frac{R}{L} &\geq \frac{F}{P} \end{align*}\)
Men vent, kva skjedde med tangensen tenkte du sikkert no? Jau du skjønar det at her har vi med ein VELDIG liten vinkel å gjere. Vi kan då skrive
\(\tan{\frac{F}{P}} = \frac{\sin{\frac{F}{P}}}{\cos{\frac{F}{P}}} \approx \frac{\frac{F}{P}}{\cos{\frac{F}{P}}} \geq \frac{F}{P}\), der den minste moglege verdien av \(\frac{\frac{F}{P}}{\cos{\frac{F}{P}}}\) nemleg er \(\frac{F}{P}\).
Vidare får vi då at
\(\begin{align*} \frac{R}{L} &\geq \frac{F}{P} \\ \frac{L}{R} &\leq \frac{P}{F} \\ L &\leq \frac{RP}{F} \qquad \blacksquare \end{align*}\)