Begin: LogEntry0005 SolYear: 8760.94
Okay, so I think I have sensible calculations for my gas boxes, so time to put that knowledge into more theory! I am still far away from building this stuff myself, I'd need to expand my factory significantly, which I intend to do, but for now I can work in the theoretical, and try to see if I can get away from this planet.
It appears that my autonomous robots has some way to verify my work, no idea how they do it, and I wish I could just access that knowledge, but for some reason it's encrypted in a way I can't figure out how to break.
Nevertheless, I started by figuring out the local force of gravity on my planet, also known as little \(g\)(or \(guh\)), this can be found quite easily using the equation \(g(r) = \frac{Gm}{r²}\), where \(G\) is the gravitational constant(\(G = 6.6743015 * 10^{-11} [m^{3}kg^{-1}s^{-2}]\)), \(m\) is the planet's mass and \(r\) is the distance from the local center of mass(usually just the center of the planet).
But how do I know the planet's mass you ask? Well there are a lot of clever ways of figuring this out, and after trying to work some of these out, one of my robots poked me, and gave me a list containing a lot of information about the solar system, including planetary masses. How do they know this? I have no idea, they apparently know where I am, and lots of other information about the planetary system, but I only have access to a fraction of it. GAAAHH! Well, I guess I have no choice but to live with this, and use what I have to figure out how to get out of here. My \(guh\) turns out to have a value of \(g = 8.90 [ms^{-2}]\), so with this I can now work further.
So, for me to even achieve lift off from the ground, my rocket has to have thrust that makes it's acceleration greater than my \(guh\), so to do this, I make sure that the mass of my spaceship plus the mass of the fuel is not too great compared to the thrust. Put mathematically it becomes \(\frac{F_{thrust}}{m_{ship} + m_{fuel}} - g > 0\). I could choose another number greater than 0, but since my robots do my calculations and are set to stop if I run out of fuel, I don't see it as a problem.

Since I've found a way to make trees, I don't really have to worry about running out of paper anymore, so I'm just going to keep calculating without worrying.
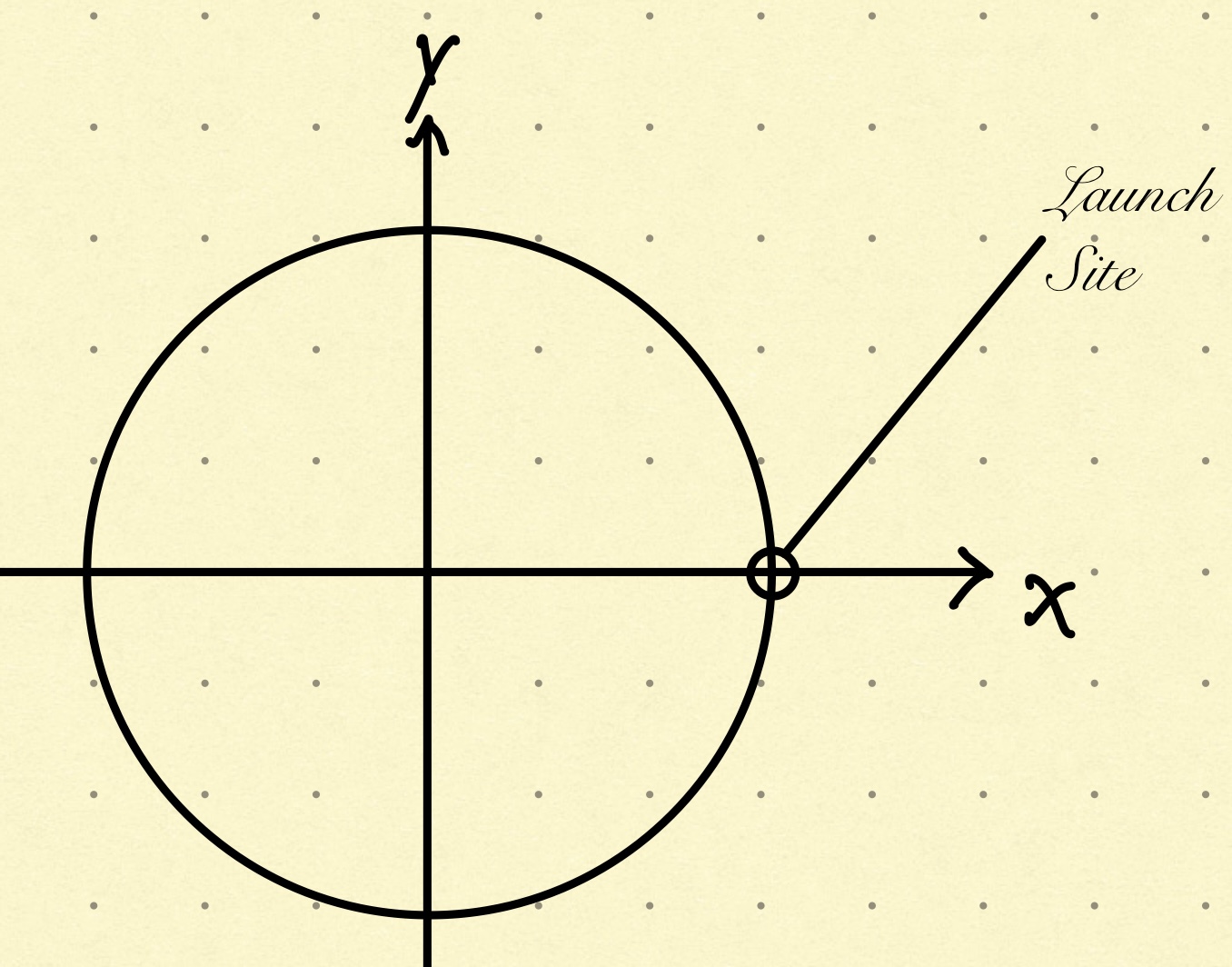
I think it's relevant to point out where I'm going to calculate my theoretical launch from. I'm setting up an \(x,y\) coordinate system, with the center of my planet as the origin, and a circle with radius \(r_{planet}\) which is equal to my planet's radius.
I'm going to launch from the point \(\vec{r_0} = (r_{planet},0)\), now since my rocket is going to be flying away from the planet, the local \(guh\) affecting my rocket will be changing with the rocket's changing position, the acceleration produced by the rocket will also be changing based on the rocket's decreasing fuel mass(fuel is ejected to push us out, so it will have to decrease).
So, now I can put my rocket's acceleration into an equation \(\vec{a_{n}} = \Big( \frac{F_{thrust}}{m_{rocket} + m_{fuel}} - g(r_n)\Big) \hat{u}_r \), where \(a_n\) is the acceleration at time step \(n\), \(r_n\) is the distance from the rocket to the planet's center of mass at time step \(n\), and \(\hat{u}_r\) is the unit vector pointing in the direction of my rocket.
When I simulate this launch, this equation has to be calculated for every timestep, my distance to the center of mass of the planet \(r_n\) should hopefully be increasing, and the mass of my fuel \(m_{fuel}\) should be decreasing in a controlled manner, hopefully. ./FingersCrossed!
On this planet there is a day & night cycle, meaning it's not tidally locked with the star it orbits, so I actually also have to take into account the angular velocity of my planet.
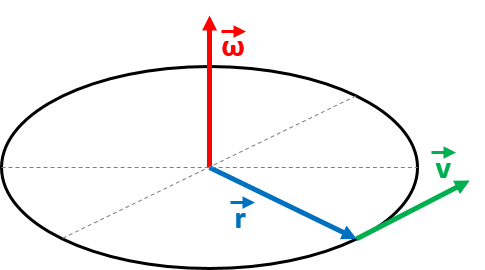
It's quite easy to figure out how this angular velocity adds to my rocket's velocity!
From the figure I can argue that \(\vec{v}_{lin} = \vec{\omega} \times \vec{r}\). In my case my \(\vec{\omega}\) will have the value \(\vec{\omega} = (0, 0, \omega_n)\), but since my launch won't affect the rotation of my planet in any way, I set \(\omega_n = \omega_0\), where \(\omega_0\) is the angular velocity of my planet.
My position \(\vec{r}\) will have the value \(\vec{r} = (x_n, y_n, 0)\), where \(x_n\) and \(y_n\) is my rocket's \(x\) and \(y\) position at timestep \(n\). Taking the cross product to find \(\vec{v}_{lin} \), I get \(\vec{v}_{n,lin} = (-\omega_0 y_n, \omega_0 x_n, 0)\), which I too will have to calculate at each timestep.
Now as I calculate my velocity at timestep \(n\), it will look like \(\vec{v}_{n+1} = \vec{v}_{n} + \big( \vec{a}_{n} * dt \big)\), and the total velocity at timestep \(n\) will be \(\vec{v}_{n, tot} = \vec{v}_{n} + \vec{v}_{n,lin}\), which finally let's me calculate the position at timestep \(n\) with \(\vec{r}_{n+1} = \vec{r}_{n} + \big( \vec{v}_{n,tot}*dt\big)\).
But when will I be far enough away from my planet to have escaped it's grasp? It doesn't really matter, all I need to do is to get fast enough to escape the planets grasp! Basically, I need to reach a velocity \(v = |\vec{v}|\), that's faster than my planets escape velocity!
The escape velocity can be calculated from the equation \(v_{esc} = \sqrt{\frac{2GM}{r}}\), where \(G\) again is the gravitational constant, \(M\) is the mass of the planet I want to escape from and \(r\) again is the distance to the center of mass of the planet. I could recalculate this for each timestep, since it will be slightly smaller the higher I get, but I've decided to not do this, since I think it's safer to make sure I reach the escape velocity found on my planet's surface. Calculating it for my planet I get an escape velocity of \(v_{esc} = 10737 [ms^{-1}]\), nearly 11 kilometers per second, man that is fast!
So I'm basically going to be simulating my launch, recalculating my acceleration from rocket thrust at each timestep, recalculating the little \(guh\) at each timestep, and adding the angular velocity from my planet's rotation at every timestep, and only stopping when I reach my planets escape velocity!
Seems pretty simple, I managed to get this set up, and set my robots calculating away, and asked them to verify that my calculated position in the solar system was correct, but they just threw their little arms in the air and shook their "heads" back and forth.
I was certain my work was correct! What nonsense is this!
After taking a little cry, and venting some frustration by "cleaning" my territories, I went back to the calculations. After lots of thinking, and a gentle prod from one of the robots pointing out the information about my planet's movement in the solar system, I realized my mistake!
I had not taken into account how my planet would move in relation to the solar system, during my launch! After rerunning my simulations, and taking into account my planet's movement in the solar system, when I asked them to verify my work, they confirmed I had done it right! They even fired off some confetti, which I have no idea where they got from, in celebration!
Just a note for myself, all of the data about my planets are given in astronomical units, and years, so my orbital velocity is given as \(\vec{v} [AU yr^{-1}]\), and I need to convert these units down to the meters and seconds I've used for my other work, or convert that work into AU and years and do it that way. I tried both ways, just to be safe, and it all worked out!
Phew, now that I know I can theoretically get off this planet, I have to make my rocket and that will take a lot of work!
End: LogEntry0005
Angular velocity figure is sourced from: https://www.omnicalculator.com/physics/angular-velocity