Hva kan disse fancy instrumentene gjøre? Glad du spurte! De kan nemlig finne nøyaktig distanse til alle planetene og stjernen rundt oss fra hvor vi er. Den trekker også fra radiusen til planeten og slik vi får senteret av planeten eksakt, luksus! Siden vi allerede vet hvordan planetene vil bevege seg i sine baner kan vi finne ut hvor de er til enhver tid. Hva kan så dette si oss om posisjonen vår?
La oss starte med at vi vet at vi er en viss distanse fra en planet, dette sier oss at vi kan befinne oss i en viss sirkelbane rundt planeten. Vet vi to distanser, kan vi så vite to mulige posisjoner da disse sirklene krysser hverandre og danner to punkter. Har vi en tredje, finner vi hvilken av de to posisjonene vi kan befinne oss i. Alt dette er illustrert under:
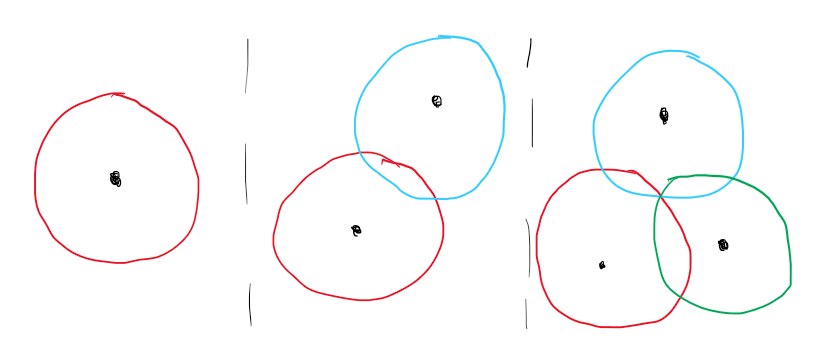
I midten: Mulige posisjoner fra to himmellegemer gir to posisjoner.
Til høyre: Mulig posisjon fra tre himmellegemer gir en posisjon.
Vi kaller denne prosessen for trilaterasjon, dette er faktisk akkurat hvordan en GPS fungerer. Tre satellitter måler avstanden til telefonen din, og finner din nøyaktige posisjon. Matematisk uttrykker vi den mulige posisjonen som hvor differansen mellom de to sirklene er null. Dette gir oss en linje, men hadde vi kun brukt to sirkler, får vi et uttrykk for y som vi kan sette inn i sirkellikningen og gitt oss en andregradslikning. ABC-formelen ville så gitt to punkter som er hvor sirklene krysser. Så vi finner de differansene mellom den tredje sirkelen som er null som gir oss enda en linje. Disse vil krysse hverandre i punktet som er posisjonen vår.
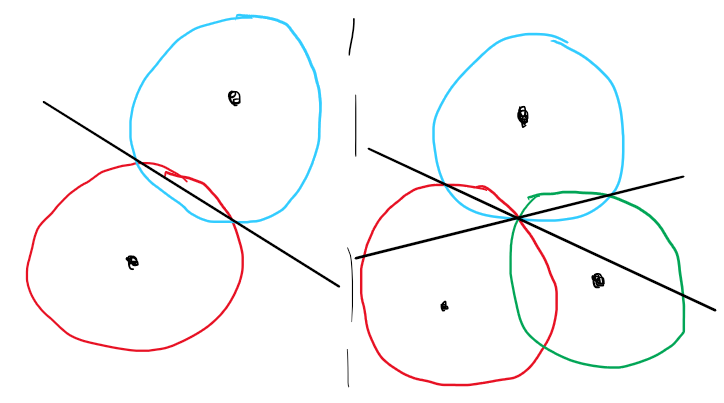
Til høyre: Disse to linjene vil krysse hverandre i et enkelt punkt (X marks the spot!).
Dette er så to likninger på formen \(y = ax + b\)*, med to ukjente (x og y i posisjonen vår!). Disse kan vi så sette inn i en av sirkellikningene og få vår eksakte posisjon. Ganske brukbart eller hva? La oss nå bruke denne metoden til å løse for våres faktiske posisjon, dette skal vise seg å være litt mer komplisert enn det høres ut som.
* Vil du sjekke at dette resultatet er sann, prøv gjerne å sette opp likningen \(sirkel_1 - sirkel_2 = 0\) gitt sirkellikningen \((x-x_1)^2 + (y-y_1)^2 = r^2\) hvor \((x_1, y_1)\) er sentrum av sirkelen.
Her er tre sirkler du kan eksperimentere om resultatet blir riktig: \((0,0),\:(6,0),\:(3,3)\) hvor alle har radius 3.
Hvordan kan vi så bruke dette til å finne vår posisjon? Hvis vi setter inn posisjonene til planetene våre med x og y koordinater, og hvor langt unna vi er fra planeten, vil vi få en sirkel med en radius som forteller oss hvor langt vekk fra planeten vi er. La oss bruke instrumentet til å få noen målinger:
| Stjernen vår | Planet 2 | Planet 5 | |
|---|---|---|---|
| x (AU) | 0 | -10.87767 | -68.22138 |
| y (AU) | 0 | -97.45891 | -7.41016 |
| r (AU) | 7.57466 | 99.19044 | 76.15741 |
Vi bestemmer oss for å lage et program som løser algebraen for oss fordi det er mye enklere å gjøre endringer og bytte himmellegemer vi bruker for å løse for posisjonen vår på en datamaskin, i teorien skulle det ikke ha noe å si, men prosessen som har fått oss så langt viser seg å ha noen veldig små avvik som Python (det programmeringsspråket vi bruker) legger merke til og gir rare svar på.
Setter vi opp to likninger, velger tre vilkårlige planeter og lar datamaskinen løse likningsettet, gir det oss nemlig imaginære tall. Får du imaginære tall i matematikken hvor det bør være reelle tall betyr det enten at du har funnet en løsning som er revolusjonær, eller, beklageligvis, i vårt tilfelle at det finnes ingen løsning.
Hvorfor? Det har seg slik at datamaskiner er ganske nøyaktig, alt for nøyaktig. Dette gjør at selv om noe er \(0.99999999....\) så vil ikke maskinen bare si at det er 1. Det må vi fortelle den. I våre beregninger hvor vi har numerisk funnet ut planetbanene våre, er det klart at det vil være små avvik. Dette avviket har Python fått snusen på og tatt med i sine beregninger. La oss plotte disse sirklene våre i GeoGebra og se hva som går galt:
så vil ikke maskinen bare si at det er 1. Det må vi fortelle den. I våre beregninger hvor vi har numerisk funnet ut planetbanene våre, er det klart at det vil være små avvik. Dette avviket har Python fått snusen på og tatt med i sine beregninger. La oss plotte disse sirklene våre i GeoGebra og se hva som går galt:
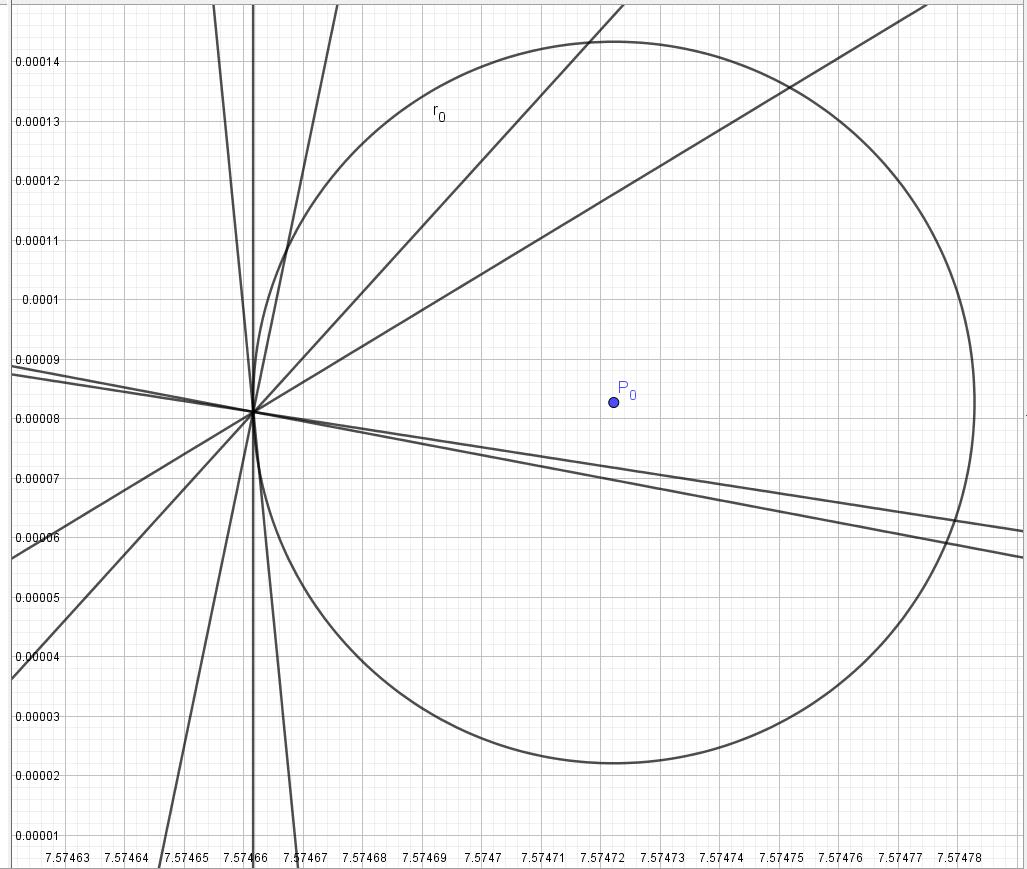
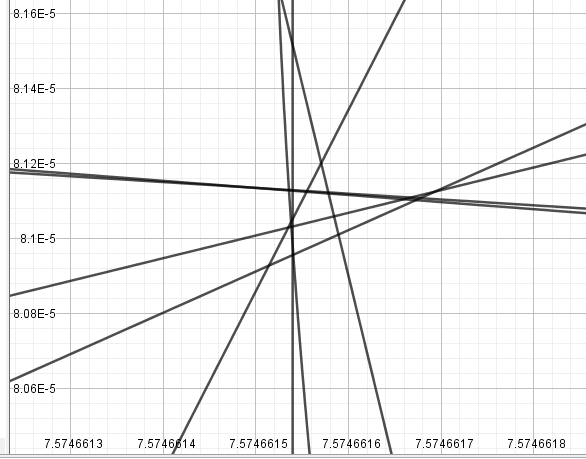
Som vi kan se, virker det som om at alle linjene krysser hverandre til et punkt, men når vi zoomer langt nok inn viser det seg at de ikke krysser hverandre i et enkelt punkt. Det forteller oss at noen tall må være gale, fordi vi er jo en viss distanse fra en planet men det har seg at den kombinasjonen vi har ikke skal eksistere! Siden denne feilen er så liten, ber vi bare Python om å få posisjonen vår gitt i reelle tall, og da finner den ut posisjonen vår til å være \(x=7.57465 \mathrm{AU}, y=8.02497\cdot10^{-5}\mathrm{AU}\), som ikke er langt ifra vår faktiske posisjon på \(x=7.57466\mathrm{AU}, y=8.06666\cdot10^{-5}\mathrm{AU}\) som gir oss en relativ feil på x-koordinaten på 0.00002% og på y-koordinaten på 0.5%.
Hva kunne vi ha gjort får å minimalimere feilen planetbanene gir? Det kan lønne seg å velge planeter som ikke beveger for mye på seg, ettersom feilen på dens bane vil være mindre enn planetene nærmest stjernen (Husk Keplers andre lov om distanse fra stjerna og omløpstid!). Dette er fordi det er mindre feil "leap frog"-metoden som vi brukte i simuleringen av planetbanene kan ha gjort på samme tid en planet som har bevegd seg lite i forhold til en som har bevegd seg langt. Merk en numerisk metode vil ikke alltid gi posisjonen helt eksakt! Siden vi har plassert stjernen vår i origo, er dette et perfekt himmellegeme for å minimere feilen. Samtidig kan de to ytterste planetene våre 5 og 2 hjelpe oss.
Forrige innlegg finner du her