Den stereografiske transformasjonen er gitt matematisk ved:
\(X = \kappa \sin{\theta}\sin{\phi-\phi_0} \)
\(Y = \kappa\left( \sin{\theta_0}\cos{\theta}-\cos{\theta_0}\sin{\theta}\cos{(\phi-\phi_0)}\right) \)
\(\kappa =\frac{2}{1+\cos{\theta_0}\cos{\theta}+\sin{\theta_0}\sin{\theta}\cos{(\phi-\phi_0)}}\)
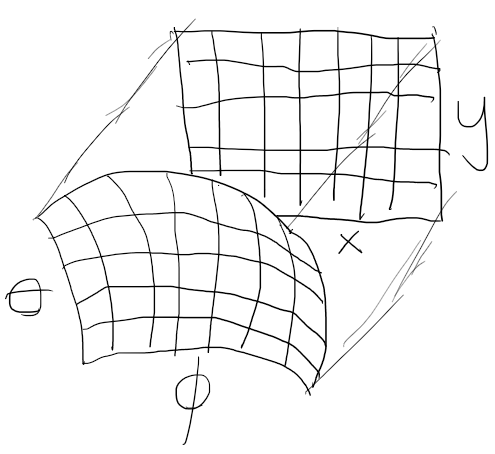
Dette virker egentlig forferdelig, men du trenger ikke å huske eller vite hvorfor, for da hadde vi nok blitt her hele dagen! Vi vil bare trikse og mikse med algebraen for å se om vi kan lage oss en intuisjon om hvor stort bildet vårt kommer til å bli. Vi transformerer et bilde gitt med \(\phi\) på x-aksen og \(\theta\) på y-aksen til det vi kjenner. Disse er begge vinkler som om man ser på overflaten av en kule, som vi prøver å strekke ut til at vi får et flatt plan med de kjente x og y verdiene som en skalar som vi må gange med en kjent enhet. Vi vet jo ikke hvor stor distanse en grad går over, så vi vil kun få en skalar.
La oss se på noe lettere å forstå. Synsvinkelen er så gitt ved differansen av den minste og den største vinkelen målt, er du enig?
\(\alpha_{\phi} = \phi_{max}-\phi_{min} \\ \alpha_{\theta} = \theta_{max}-\theta_{min}\)
Midt i mellom maks- og minimumsverdien ligger null, dette tilsvarer midten av bildet. Dette vil så si at differansen fra enten maks- eller minimumsverdien vil gi halve synsvinkelen.
\(-\frac{\alpha_{\phi}}{2} \leq \phi - \phi_0 \leq \frac{\alpha_{\phi}}{2} \)
\(-\frac{\alpha_{\theta}}{2} \leq \theta - \theta_0 \leq \frac{\alpha_{\theta}}{2}\)
Setter vi maks- og minimumsverdien \(\phi\) kan ha i likningen for X vil vi så få:
\(X_ {max/min} = \kappa \sin{\theta}\sin{\pm\frac{\alpha_{\phi}}{2}} \)
Det er egentlig løsningen, ikke vanskelig eller hva? Vi kan likevel forenkle uttrykket slik at maks- og minimumsverdien til X kun er avhengig av synsfeltet. La oss først bli kvitt leddene med \(\theta\), dette kan vi gjøre ettersom at synsfeltet i y-retning ikke har betydning for synsfeltet i x-retning. Vi setter \(\theta\) i Y = 0, eller når \(\theta = \theta_0 = \frac{\pi}{2}\):
\(X_ {max/min} = \kappa \sin{\pm\frac{\alpha_{\phi}}{2}} \)
Som du kanskje husker fra ovenfor, så er jo \(\kappa\) full av trigonometriske uttrykk som inneholder både \(\theta\) og \(\phi\) i seg! La oss se om vi kan forenkle uttrykket mer:
\(X_ {max/min} = \frac{2\sin{\pm\frac{\alpha_{\phi}}{2}} \sin{\pm\frac{\alpha_{\phi}}{2}}}{1+\cos{\theta_0}\cos{\theta}+\sin{\theta_0}\sin{\theta}\cos{\pm\frac{\alpha_{\phi}}{2}}} \)
Vi ser nemlig at \(\cos{\theta_0}\cos{\theta}\) blir 0, og at \(\sin{\theta_0}\sin{\theta}\) blir 1:
\(X_ {max/min} = \frac{2\sin{\pm\frac{\alpha_{\phi}}{2}} \sin{\pm\frac{\alpha_{\phi}}{2}}}{1+\cos{\pm\frac{\alpha_{\phi}}{2}}} \)
Nå som vi har funnet uttrykket for maks- og minimumsverdien til X, er det kun naturlig at vi finner maks- og minimumsverdien til Y. Vi starter på samme måte, og antar at \(\phi = \phi_0 = 0\):
\(Y_ {max/min} = \kappa\left( \sin{\theta_0}\cos{\theta}-\cos{\theta_0}\sin{\theta}\cos{(\phi-\phi_0)}\right) \)
\(Y_ {max/min} = \kappa\left( \sin{\theta_0}\cos{\theta}-\cos{\theta_0}\sin{\theta}\right) \)
Gjenkjenner du den trigonometriske identiteten for \(\sin{(u-v)}\)? Litt trigonomagi gir jo selvfølgelig at:
\(Y_ {max/min} = \kappa\sin{\theta-\theta_0} \)
\(Y_ {max/min} = \kappa\sin{\pm\frac{\alpha_{\theta}}{2}} \)
La oss så sette inn \(\kappa\) og se hvor langt vi kommer:
\(Y_ {max/min} =\frac{2\sin{\pm\frac{\alpha_{\theta}}{2}}}{1+\cos{\theta_0}\cos{\theta}+\sin{\theta_0}\sin{\theta}\cos{(\phi-\phi_0)}} \)
\(Y_ {max/min} =\frac{2\sin{\pm\frac{\alpha_{\theta}}{2}}}{1+\cos{\theta_0}\cos{\theta}+\sin{\theta_0}\sin{\theta}} \)
Her er det to muligheter, grine over at trigonometrien er fæl, eller se om vi har noen andre trigonometriske identiteter vi kan grave frem. Som fysikere, velger vi å gjøre begge, og vi vet så identiteten for uttrykket på bunnen er \(\cos{(u-v)}\).
\(Y_ {max/min} =\frac{2\sin{\pm\frac{\alpha_{\theta}}{2}}}{1+ \cos{\theta-\theta_0}}\)
\(Y_{max/min} = \frac{2\sin{\pm\frac{\alpha_{\theta}}{2}}}{1+ \cos{\pm \frac{\alpha_{\theta}}{2}}}\)
Dermed har vi vist maks- og minimumsverdien til X og Y, gitt synsfeltet.
Forrige innlegg kan du finne her
og for neste finner du her