I dette forsøket vil vi se på hvordan lys blir påvirket nærme et sort hull ved å tenke oss at vi har en skall observatør, observatør nærme det sorte hullet, som peker en laser radielt utover mot en langt vekk observatør. Skall observatøren er en avstand r fra sentrum av det sorte hullet og langt vekk observatøren er rett og slett ganske langt unna.
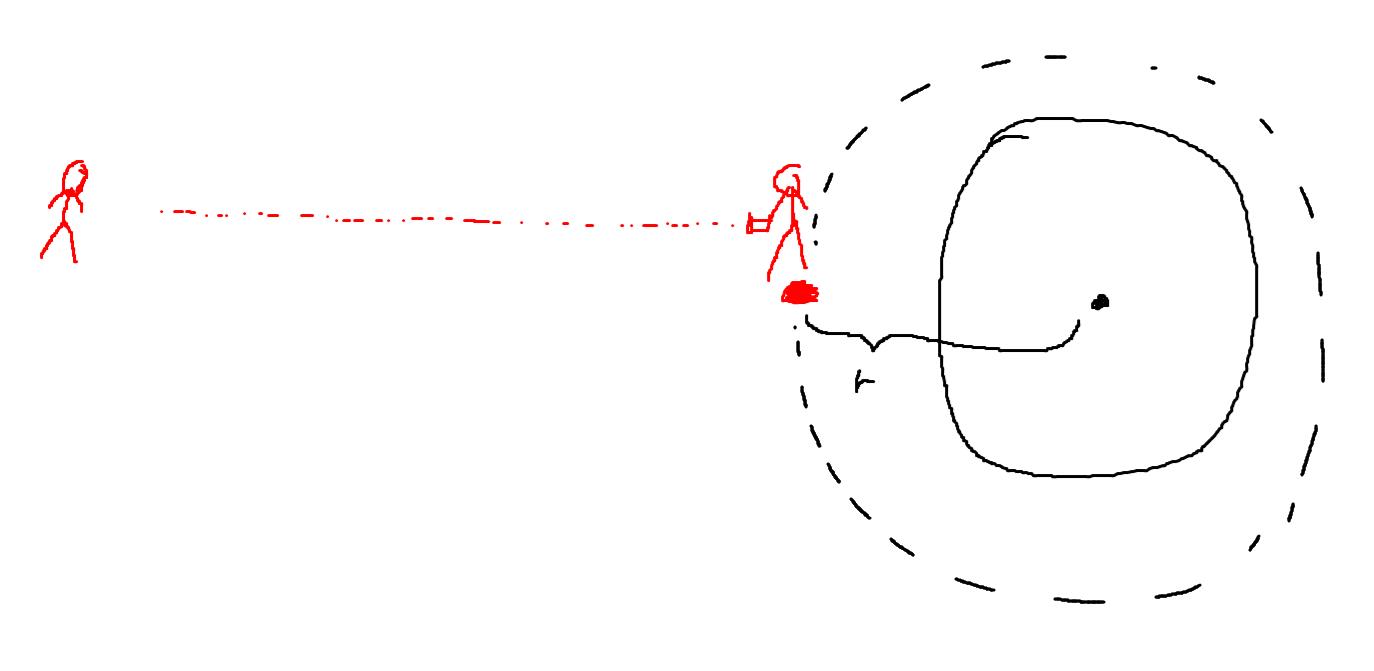
Lyset som skall observatøren sender har en bølgelengde \(\lambda_{sh}\) og vi er ute etter å finne bølgelenden, \(\lambda\) som langt vekk observatøren vil observere at det samme lyset har. Frekvensen som lyset har for skall observatøren er \(\nu_{sh}=1/\Delta t_{sh}\) og for langt vekk observatøren vil dette være \(\nu = 1/\Delta t\), her er \(\Delta t_{sh} \) og \(\Delta t\) tiden mellom to bølgetopper til lyset som blir sendt ut fra laseren.
Vi starter med å finne et forhold mellom \(\Delta t_{sh}\) og \(\Delta t\) ved å bruke noe som kalles for Schwarzschild linje element som er gitt som
\(\Delta S^2 = \left(1 - \frac{2M}{r}\right) \Delta t^2 - \dfrac{\Delta r^2}{\left(1 - \frac{2M}{r}\right)} - r^2\Delta \phi ^2\)
og bruker noe som kalles for Lorentz linje element i polare koordinater som er gitt som
\(\Delta S^2 = \Delta t^2 - \Delta x^2 - \Delta y^2 = \Delta t^2 - \Delta r^2 - r^2\Delta \phi ^2\)
Noe som er verdt å merke seg fra Schwarzschild og Lorentz linje element er at vi vil bruke polare koordinater fordi systemet vi ser på er definert som planet 2 ulike eventer skjer i, rundt en masse \(M\), dermed blir det mer naturlig å bruke polare koordinater, der origo er sentrum av massen. En annen ting som er verdt å merke seg er at \(\left(1 - \frac{2M}{r}\right)\) er dimensjonsløs. En rask dimensjonsanalyse viser dette ganske greit. Vi kan se bort fra tallet 1, for den er allerede dimensjonsløs. Det skal også ha vært \(G/c^2\) der \(G\) er gravitasjonskonstanten og c er lysets hastighet i vakuum.
\(\frac{MG}{rc^2}\Rightarrow \frac{[kg]\cdot [N\cdot m^2/kg^2]}{[m] \cdot [m/s^2]}\Rightarrow \frac{[kg]}{[m]}\cdot \frac{[kg]\cdot[m]}{[s^2]}\cdot\dfrac{\frac{[m^2]}{[kg^2]}}{\frac{[m]}{[s^2]}}\Rightarrow \frac{[kg^2]}{[s^2]}\cdot\frac{[m]\cdot[s^2]}{[kg^2]} \Rightarrow [m]\)
Så du lurer nok på hvorfor vi ikke skriver \(\left(1 - \frac{2MG}{rc^2}\right)\), kort forklart så kommer det av at fysikere ofte er late, og som en konsekvens av at vi ofte måler tid i meter. Dermed må vi være nøye med å gjøre om massen til meter før vi setter inn i uttrykket \(\left(1 - \frac{2M}{r}\right)\), så slipper vi å måtte skrive \(\dfrac{G}{c^2}\). For å gjøre om mellom masse til meter kan vi bruke
\(\dfrac{M_{masse}}{M_{meter}} = \dfrac{G}{c^2}\)
Her er \(\Delta S\) noe som kalles for tidrom elementet som sier noe om hvordan avstander er målt. \(\Delta \phi\) er forskjellen i vinklene mellom to eventer i det polare koordinat systemet.
Tilbake til det opprinnelige problemet. Vi starter med å sette \(\Delta S^2 = \Delta S_{sh}^2\), her er \(\Delta S_{sh}^2 = \Delta t_{sh}^2 - \Delta r_{sh}^2 - r^2\Delta \phi ^2\), som er for skall observatøren. Uttrykket for langt vekk observatøren blir Schwarzschild linje elementet.
\(\Delta t_{sh}^2 - \Delta r_{sh}^2 - r_{sh}^2\Delta \phi ^2 = \left(1 - \frac{2M}{r}\right) \Delta t^2 - \dfrac{\Delta r^2}{\left(1 - \frac{2M}{r}\right)} - r^2\Delta \phi ^2\)
\(r^2\Delta \phi ^2 \Leftrightarrow r_{sh}^2\Delta \phi ^2= 0\) fordi vi ser på to eventer som er på en rett linje langs den radielle komponenten fra origo, som betyr at forskjellen i vinkelen mellom dem er lik 0. På grunn av at vi ser på tiden mellom to bølgetopper for en skall observatør og en langt vekk observatør kan man sette \(\Delta r_{sh}^2 \Leftrightarrow \Delta r^2 = 0 \) for begge er tilnærmet lik null.
\(\begin{align*} \Delta t_{sh}^2= \left(1 - \frac{2M}{r}\right) \Delta t^2 \end{align*}\)
Løser for \Delta t og med litt algebra og man får vi
\(\Delta t = \dfrac{\Delta t_{sh}}{\sqrt{\left(1 - \frac{2M}{r}\right)}}\)
Da er det på tide å putte dette sammen med EM-stråling for å se hvordan det blir påvirket nært et sort hull. Vi bruker formelen for doppler skiftet gitt som
\(\dfrac{\Delta \lambda}{\lambda_{sh}}=\dfrac{\lambda -\lambda_{sh}}{\lambda_{sh}}\)
Vi bruker så at \(v = \nu \lambda\) der \(v = c = 1\) og at \(\nu = 1/\Delta t\). Vi får da \(\Delta t = \lambda\), gjør vi dette for frekvensen for skall og langt unna observatøren får vi \( \Delta t_{sh} = \lambda_{sh}\) og \(\Delta t = \lambda\). Setter vi inn dette i uttrykket for doppler skiftet får vi
\(\dfrac{\lambda -\lambda_{sh}}{\lambda_{sh}} = \dfrac{\Delta t - \Delta t_{sh}}{\Delta t_{sh}}\)
Setter vi så inn uttrykket for \(\Delta t\) får vi
\(\dfrac{\dfrac{\Delta t_{sh}}{\sqrt{\left(1 - \frac{2M}{r}\right)}} - \Delta t_{sh}}{\Delta t_{sh}}\Rightarrow \left(\dfrac{1}{\sqrt{\left(1 - \frac{2M}{r}\right)}} - 1\right)\cdot\frac{\Delta t_{sh}}{\Delta t_{sh}}\)
\(\dfrac{\Delta\lambda}{\lambda_{sh}} = \dfrac{1}{\sqrt{\left(1 - \frac{2M}{r}\right)}} - 1\)
Nå er vi interessert i å se hva som skjer når \(r>> 2M\). Når \(r>> 2M\) blir alt under brøken veldig lite, så da kan vi gjøre noen tilnærmelser ved hjelp av noe som kalles for taylor utvikling. Kort forklart så lager man et polynom rundt et punkt som man kan bruke som en tilnærmelse. Hvis du vil ha en mer detaljert forklaring så kan du gå til 3Blue1Brown sin video om det som du kan finne her.
Vi setter først at \(x = 2M/r\) og gjør rekkeutviklingen for \(1/\sqrt{1-x}\) rundt \(0\) og får for første orden
\(f(x) \approx 1 + \frac{x}{2} + O(x^2) \)
Setter vi inn for \(x\) får vi at
\(\dfrac{1}{\sqrt{\left(1 - \frac{2M}{r}\right)}} = 1 + \frac{2M}{2r} \Rightarrow 1 + \frac{M}{r}\)
\(\dfrac{\Delta\lambda}{\lambda_{sh}} = \dfrac{1}{\sqrt{\left(1 - \frac{2M}{r}\right)}} - 1 \Rightarrow 1 + \frac{M}{r} - 1 \Rightarrow \frac{M}{r}\)
Vi kan dermed si at dobbler skiftet lys fra en skall observatør er \(\dfrac{\Delta\lambda}{\lambda_{sh}} = \dfrac{M}{r}\)