Hvorfor er det ikke realistisk å anta at vi kan komme oss til destinasjonen vår med å reise i en rett linje? Selv om alle planetene og vår egen stjerne ligger langt unna, så vil tyngdekraften fra hver av dem virke på raketten til enhver tid. Så om vi ikke kan lage en rett linje, og si at det er slik vi skal komme oss frem, hvordan skal vi da kunne planlegge reisen i forkant?
Det er et par antagelser vi tar som er ganske relevant for å skjønne hvilken utfordring vi står overfor. Første er at vi kan skyte opp raketten når vi vil og fra hvor som helst på overflaten av planeten. Dette gjør at vi kan justere vinkelen, og tidspunktet som vi sender opp raketten for å få den til vår destinasjon. Vi har begrenset med drivstoff, som betyr at det er en begrenset ressurs som kan spille en viktig rolle til senere. For hver manøver vi gjør som krever en form for ekstra framdrift i en gitt retning, vil alltid bruke opp drivstoff. Det betyr at vår evne til å bevege oss fritt er begrenset til mengden av drivstoff, det er derfor ønskelig å spare så mye drivstoff som mulig. I vårt tilfelle så har vi rundt 1058 kg drivstoff til vår disposisjon, dette burde holde for en relativt god stund. Noe annet som blir utrolig viktig i starten av reisen er størrelsen av tidsstegene. Dette er innviklet og krever sitt eget avsnitt.
Vi kan tenke oss at vi deler opp hele reisen i mindre steg, og måler den totale kraften som virker på raketten i hvert tidssteg, ved at vi bruker posisjonene til planetene for den gitte tiden og måler avstanden til hver av dem for å finne kraften og akselerasjonen. Denne akselerasjonen er den vi bruker for å flytte på raketten den avstanden og retningen for det gitte tidssteget. Dette er det samme konseptet vi har brukt i tidligere simuleringer av planetbanene. Eneste forskjellen er at vi legger sammen hver av de individuelle kreftene fra legemene i systemet, og bruker summen av disse for å flytte på raketten. Vi kommer igjen til å bruke leap-frog for vår numeriske løsning, fordi, som ble nevnt i simulering av planetbanene, så har den egenskapen at den bevarer energien i systemet, som er viktig i dette tilfelle. Grunnen til dette er at dersom energien i systemet ikke er bevart så vil raketten avvike fra sin faktiske bane, som mest sannsynlig resulterer i at den faller inn mot stjernen under simuleringen. Denne usikkerheten er noe vi definitivt ikke ønsker når presisjonen er det som er hovedprioriteten.
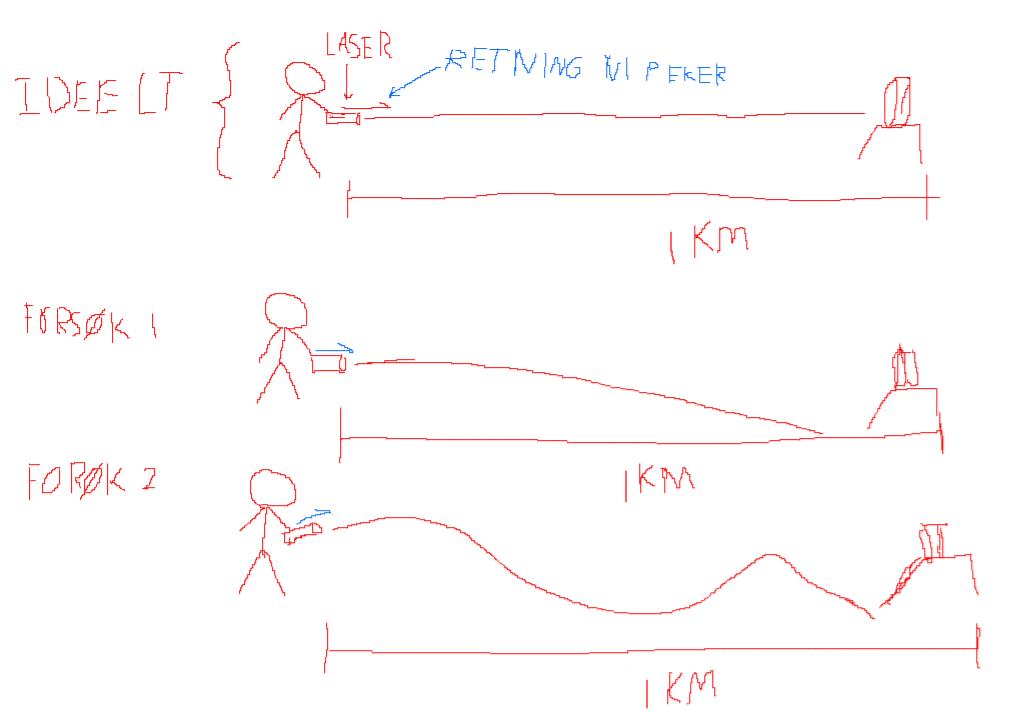
Presisjon er ønskelig fordi det blir som om vi skal peke en laser på en ca 10 cm i diameter, stor sirkel over en avstand på 1 km. Dette er da vanskelig nok i seg selv, men så legger vi til en avbøyning, uten at vi vet hvor mye lyset fra laseren vil avbøyes. Alt vi vet er at det bøyes mot en retning. Som man nå ser så er det vanskelig å forutse hvor lyset faktisk lander, så man blir nødt til å justere avhengig av våre observasjoner.
Antall legemer vi tar med under de numeriske utregningene må også vurderes. Tanken er at gitt newtons gravitasjons lov, der \(G\) er gravitasjons konstanten, \(M\) er massen til legemet vi måler kraften fra, og \(m\) er massen til raketten.
\(F = \frac{GMm}{r^2}\)
F er som sagt kraften som virker på raketten som gir at \(F = am\), som betyr at når vi setter dette lik hverandre så vil vi stå igjen med akselerasjonen for raketten, fra et gitt objekt.
\(F = \frac{GM}{r^2}\)
Viktig å merke seg er at vi bruker at \(G = 4\cdot \pi^2\) og \(M \) er målt i solmasser på grunn av at vi bruker AU og yr som enheter. Det som er viktig å merke seg er forholdet mellom kraften, eller akselerasjonen, fra et objekt i en gitt avstand \(r\). På grunn av at vi har \( r^2\) så betyr det at kraften er omvendt proporsjonal med kvadratet av \(r\). I praksis betyr det at kraften på et objekt minker med en faktor på \(4r\). Dette betyr at vi kan se bort fra kraften fra de planetene som ligger lengst unna, fordi det er snakk om en avstand på 25 AU+.
Etter å ha sett nærmere på størrelsen på kreftene fra disse planetene på raketten, konkluderte vi med at de så å si hadde den samme verdiene som de andre steinplanetene. Grunnen til dette er at de er såpass massive, som gjør opp for de store avstandene og som putter dem i samme boks som de andre indre planetene, når det kommer til påvirkning på raketten. Den man kunne ha sett bort ifra, basert på kraften alene, er faktisk den innerste planeten, men på grunn av at vi kan ende opp med å fly ganske nærme denne planeten, gjør at vi ikke kan utelukke den.
Størrelsen for tidsstegene er også ganske viktig å ta hensyn til, for større tidssteg vil gi større avvik. La oss si at du skal dele en halvsirkel i n antall like store deler. For hver del setter du nå et punkt, og hver ende vil alltid ha et punkt. Så å trekker en linje mellom hvert punkt, slik at du ender opp med en oppdelt linje som skal tilsvare bevegelsen gitt for n antall tidssteg som blir brukt. Si at n = 2 og du ender opp med noe som ikke likner i det hele tatt på en halvsirkel. La oss nå øke n med 10, og du vil ende opp med noe som likner mer på en sirkel, men som fremdeles ikke er en perfekt halvsirkel, for det krever at n er uendelig. Dette er jo noe som har blitt tatt opp tidligere, så hvorfor blir det nevnt igjen?
La oss endre perspektiv, og se på n antall oppdelinger som n antall tidssteg. Vi kan allerede kaste ideen om å ha uendelig mange, eller utrolig små tidssteg, for da kommer vi ingen vei. Har vi for store får man mye usikkerhet og avvik, så det gjelder å ha passe store tidssteg. Når raketten er nærme en planet vil kraften fra denne planeten bli mye større enn den totale kraften fra de andre planetene. Dette fører til at de numeriske utregningene blir feil, fordi den vil tro at raketten blir påvirket av en stor kraft, i lengre tid enn den faktisk blir, på grunn av størrelsen av tiddsteget. Man får på mange måter hakk i utregningen, for kraften fra denne planeten går ned gradvis, men med store steg får man ikke den jevne avtagelsen. For å fikse dette vil vi bruke noe som kalles for interpolasjon. Interpolasjon er at vi ser på posisjonene til to punkter, eller planetene, mellom to tidssteg, for så å dele det opp i nye punkter, men i form av en parametrisering. Dette gjør at man kan sette inn en verdi mellom de to nærmeste tidsstegene, og få ut posisjonen som planeten ville ha vært i på det gitte tidspunktet. Dette gjøres for alle planetene og blir brukt i den første tiden etter at raketten har nådd verdensrommet.
Det vi endte opp med å gjøre var å kjøre simuleringen i en bestemt tid, der vi brukte de interpolerte posisjonene til planetene. Antall tidssteg for oss ble 50000 sekunder, med størrelsen på tidsstegene på 1 sekund, eller 1/yr. Tanken bak dette var å gi raketten nok tid til å komme langt nok unna til at kraften fra hjemplaneten ble mer tilsvarende som kreftene fra de andre planetene. Planen var egentlig å si at vi stopper interpolerings-prosessen så fort kraften fra hjemplaneten ble like stor som kraften fra stjernen. Dette visste seg å bli være litt vrient, ikke i forhold til implementering i seg selv, men problemet med at dette ville gjøre at koden ville bruke mye mer tid i forhold til en bestemt mengde tid. Selve antall sekunder ble bestemt etter mye testing, der vi fant ut at det holdt med 20 000, for at raketten ikke ble skutt ut i en tilfeldig retning. Rundt 30 – 40 tusen før resultatene ble mer naturlig, men rundt 40 000 ble ansett som antallet som var nødvendig før raketten gjorde det den skulle i de aller fleste tilfeller. Så de ekstra 10 tusen stegene er ment som et slingringsrom for å øke sikkerheten.
Etter at interpolerings-prosessen er ferdig sender vi posisjonen til planetene og raketten videre til hoveddelen som fortsetter der den første slapp, men med normale tidssteg. Deretter lar vi raketten drifte i en bestemt tid, som vi bare måtte teste oss frem til. Grunnen var at vi ikke visste hvor lang tid reisen ville ta. Underveis så sjekket vi også for når raketten var på det nærmeste, notere ned hvilken vinkel og tid vi brukte. Deretter var det å finne hvilken kombinasjon som gjorde at vi kom nærmest vår destinasjon.