Det er to spesifikke handlinger som er aktuelle for oss. Den første er å bare la raketten fly gjennom verdensrommet uten noe direkte inngrep som korreksjoner, den andre handlingen er at vi bruker rakett motoren for å gi oss et ekstra boost i en forhåndsbestemt retning. Disse to blir kalt for coast, og boost. Det er ingen spesifikk metode vi har brukt for å bestemme hvor mye vi trenger å booste for å komme inn i den planlagte kursen om vi skulle få avvik, utenom å prøve oss frem for å komme noenlunde innenfor et akseptabelt avvik. Noe som er viktig å ha i bakhode er at en boost varer såpass kort at vi kan anta at det skjer med en gang, dette gjør at vi ikke trenger å tenke over den delen i noe særlig stor grad. Dette er da noe vagt, men målet her er ikke å holde kursen helt perfekt, men å komme inn foran planeten og være så nærme som mulig så lenge som mulig før vi setter i gang ned bremsingen. Så målet er mer å treffe innenfor et generelt område enn å stadig skulle gjøre små justeringer.
Dette kan virke litt motsigende i forhold til det vi tidligere har sagt om presisjon. Grunnen til at presisjonen ikke har like stor rolle her er at vi har disponert drivstoff til å utføre en ressurskrevende manøver, som betyr at vi har rom til å satse litt. Om vi så må booste litt ekstra for å ta igjen planeten, eller om vi må bremse for å ikke fly forbi, så blir vi nødt til å bruke store deler av drivstoffet vårt. Dette er definitivt noe som ikke kan bli planlagt i like stor grad i forkant i forhold til tidligere og krever dermed justeringer underveis.
I motsetning til tidligere så gikk utføringen av selve reisen ganske problemfritt. Mest sannsynlig så var det et resultat av litt flaks, men også på grunn av planleggingen i forkant. Vår reise ble dermed som følger.
- coast(50000/yr)
- boost(-0.2145, 0.00129588), ca 236.9 kg drivstoff brukt opp
- coast(5.86)
- boost(-0.0063, 0), ca 6.9 kg drivstoff brukt opp
- coast(1)
- boost(0.01, 0.006), ca 12.7kg drivstoff brukt opp
- coast(1)
- boost(0.008, -0.021), ca 24.3 kg drivstoff brukt opp
- coast(2.0079)
- coast(0.0004516285)
- boost(0.42, -0.23), ca 411.3 kg drivstoff brukt opp
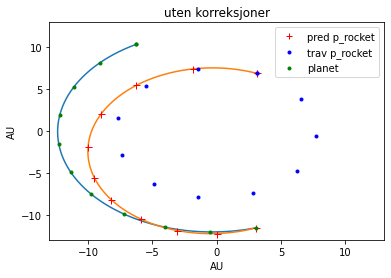
Det første som er å ikke gjøre noe er for å kompensere for tiden som ble brukt til interpoleringen under simulasjonen. Etter denne er over burde vi ha vært der vi var under simuleringen, men dette var ikke tilfelle, for vi var lenger bak enn planlagt og med mindre fart. Dette resulterte i det man kunne se i bildet over. Vi ble dermed nødt til å øke farten så vi ikke falt så mye inn mot stjernen. I dette tilfelle la vi på differansen mellom hastigheten fra simuleringen på det gitte tidspunktet i forhold til det vi hadde under reisen. Neste nødvendige inngrep som ble gjort var etter 5.86 år, hvor vi bare sørget for å komme sånn cirka inn på den planlagte kursen. Det samme kan sies om de to neste gangene, punkt 6 og 8, som skjedde en gang hvert år for 2 år. Etter det kommer en rekke mer, tilsynelatende tilfeldig valgte tider.
Den første som er nr 9, kommer fra at det er tiden fra forrige manøver til det ble nødvendig å sjekke posisjonen til raketten i forhold til planeten mer hyppig. Nr 10 er tiden vi fant etter å ha sjekket ganske hyppig siden sist hvor raketten var i forhold til planeten. Akkurat som med hjemplaneten så definerte vi \(0^o \) når radien ligger parallelt i forhold til x aksen rettet i positiv x retning. Altså samme retning som enhetssirkelen. Tiden oppgitt i nr 10 er da raketten ligger så og si \(180^o \) i forhold til planeten, som ga en passende verdi å bruke for utregning av hvor mye vi måtte bremse for å ende opp i bane rundt planeten. Den siste, nr 11 er det vi kom fram til som skulle til for å gå inn i bane.
Hastigheten som skulle til for å ende opp i bane rundt planeten kan bli utledet ved å bruke Newtons gravitasjons lov, og sirkelbevegelse, for vi ønsker ideelt sett en mest mulig sirkulær bane som mulig. Setter vi de to utrykkene mot hverandre får man:
\(F = \dfrac{GM_p m}{r^2}\ og \ F = \frac{mv_{stable}^2}{r}\) som gir
\(\frac{mv_{stable}^2}{r} = \dfrac{GM_p m}{r^2} \Rightarrow v_{stable}^2 = \frac{GM_p}{r}\Rightarrow v_{stable} = \sqrt{\frac{GM_p}{r}}\)
Dette gir den tangentielle komponenten som skal til for å ha en sirkulær bane rundt planeten i en gitt avstand. Så gjelder det å finne hastigheten raketten har i forhold til planeten, for vi ønsker nå å bytte referansepunkt. Vi har tidligere brukt origo som referansepunkt, men her er vi interessert i hastigheten raketten har i forhold til et annet objekt, planeten. Dette kaller vi for \(\textbf{v}_0\) og vi finner den ved å ta differansen mellom raketten og planeten sin hastighet. Vi vet allerede \(\vec{v}_{rocket}\) ut fra instrumentene om bord på raketten. Uttrykket for hastigheten som skal til for å komme i bane er \((\Delta v)_{inj} = v_{stable} - \textbf{v}_0\).
\(V_p = \sqrt{GM_p(\frac{1}{r} - \frac{1}{a})}\), der \(a\) er semi major aksen til planeten, hvis du er nysgjerrig på hvor denne kommer fra så kan du gå hit Vis-viva_equation. \(r\) er avstanden fra planeten til brennpunktet, i dette tilfelle er det origo. Neste vi så trenger er noe som kalles for flight path angle \(\phi\), som er vinkelen mellom \(V_p\) og \(\vec{e}_\theta\), som også ligger langs den lokale horisontalen. Se bildet under for visualisering.
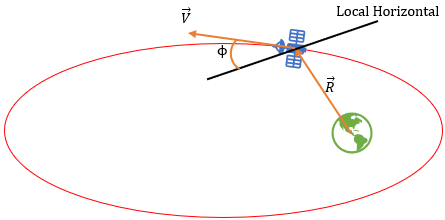
Flight path angle får vi fra \(\tan \phi = \dfrac{e \sin(\nu)}{1 + e\cos(\nu)}\ der\ \nu = \theta\), her er \(e\) eksentrisiteten for planeten, dersom du er nysgjerrig på denne så kan du gå hit Elliptic_orbit. Grunnen til at vi har gått gjennom bryet med alt dette for å finne hastigheten til planeten er at vi bare har størrelsen for farten, men det vi trenger er komponentene. For å få hastigheten tar vi først å finner vinkelen som \(V_p\) har i rommet, i forhold til vårt referansesystem som er i origo. Vi kan kalle denne vinkelen vi får for \(\alpha\), som kommer fra \(\alpha = \theta + \frac{\pi}{2} - \phi\). Kan du se hvorfor det må bli slik?
Fra enhetssirkelen er positiv retning definert som å gå mot klokken. På grunn av at brennpunktet er i origo så betyr det at \(\theta\) alltid er vinkelen mellom en gitt radius ut til en planet og x aksen mot positiv retning. \(\phi\) er vinkelen mellom \(\vec{V}\)og normalen til en linje, lokale horisonten, som står på linjen fra origo ut til en gitt legeme, planeten. Positiv retning er mot venstre, og normalt betyr at det er \(90^o\) på linjen fra origo, dette betyr at man må legge til \(\frac{\pi}{2}\) til \(\theta\). Så kommer \(\phi\) som er i motsatt retning av det, og dermed må man trekke fra. Komponentene for \(\vec{V_p} = [V_p \cdot \cos(\alpha), V_p \cdot \sin(\alpha)]\).
Nå kan vi finne \(\vec{\textbf{v}}_0 = \vec{v}_{rocket} - \vec{V_p}\).
Vi kan så finne \((\Delta \vec{v})_{inj} = \vec{v}_{stable} - \vec{\textbf{v}}_0\) der
\(\vec{v}_{stable} = [v_{stable} \cdot \cos(\theta_{rp} - \frac{\pi}{2}), v_{stable} \cdot \sin(\theta_{rp} - \frac{\pi}{2})]\)
Her er \(\theta_{rp}\) vinkelen som raketten har i forhold til planeten og grunnen til at vi trekker fra \(\frac{\pi}{2}\) er at vi vil gå i bane med klokken. Dette er vel en grei måte å gjøre det på, men virker litt kronglete i forhold til andre metoder, som å bruke radiell og tangentiell hastighets komponentene til planeten for å finne hvor fort den bevegde på seg. Dette hadde definitivt vært lettere om vi hadde visst noe mer om tiden mellom to målinger. Radiell og tangentiell hastighet er tidsavhengig og i dette tilfelle var det usikkert i hvor stor grad det ville gi det vi trengte, så derfor gikk vi omveien og brukte den metoden vist ovenfor.
Vi var en avstand på rundt \(1.89 \cdot 10^{-4} AU\) til planeten da vi bremset ned under vår siste manøver i punkt nr 11, og verdiene kommer fra utregningene ved bruk av formlene ovenfor. Tok oss bare 9.87 år men vi kom oss frem.
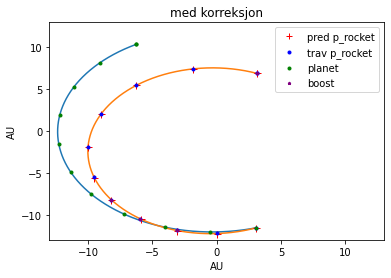
Det eneste som gjenstår da er å sjekke om vi faktisk er i bane, eller om vi bare går i bane i en midlertidig periode. Det vi gjorde var å se om vi fremdeles var i bane rundt planeten etter 4 år, noe vi var. Så vi kan vel trygt anta at vi er i en stabil bane.