Før vi kan starte med å se på stjernen vår er det 4 antagelser vi må gjøre som er følgende
- Tetthetene i stjernen vår er uniform, som betyr at tettheten er det samme uavhengig av hvor vi ser i stjernen.
- Vi skal finne trykket som om det var en ideell gass. Vi kan også ignorere faktorer som strålingstrykk.
- Vi vil anta at stjernen har hydrostatisk likevekt.
- Stjernen består bare av protoner med masse \(M_h= 1.673 · 10^{−27}\ kg\)
Dette er noen ganske store antagelser, som for eksempel at det bare finnes protoner i stjernen, eller at tettheten er uniform. På grunn av de store antagelsene så betyr det at svaret vi får ikke er helt presist sammenliknet med det som faktisk skjer i en stjerne.
Vi starter med å finne ut av hva kjernetemperaturen er. Vi vet at det skjer fusjon i stjernen, som trenger partikler som hoveddrivstoff. Det er mer komplisert enn som så, men det er en av de komponentene som skal til for å få fusjon. Vi kan da finne ut hvor mye som kan fusjoneres innenfor en gitt avstand fra sentrum av stjernen som en funksjon av \(r\). Vi finner da hvor mye masse \(M(r)\) som er i et gitt volum \(V(r) = \frac{4\pi r^3}{3}\), som er volumet av en kule, i tillegg må vi inkludere tettheten \(\rho\). Vi antar her at all masse innenfor dette området kan gå til fusjon. Setter vi dette sammen får vi et uttrykk for \(M(r)\) som blir som følger
\(M(r) = V(r)\cdot \rho \Rightarrow \dfrac{4\pi r^3}{3} \rho\) .
Vi ser nå at vi også kan finne tettheten \(\rho\), fordi tetthet er masse delt på volum, som er det vi har her. Fra den første antagelsen vet vi at \(\rho\) er konstant og uavhengig av \(r\) dermed trenger vi ikke skrive \(M(r)\) for massen, for da holder det å bare skrive \(M\). I tillegg kan det være lurt å si at det er en forskjell på variabelen \(r\) og en radius som er konstant. Dette har muligens ikke så mye å si akkurat nå, men kan godt hende at det vil spille en rolle senere. Vi vil kalle den konstante \(r_{\rho}\). Vi kan da skrive \(\rho\) som
\(\rho = \dfrac{3M}{4\pi r_{\rho}^3}\). For å finne \(\rho\) kan vi ta total masse delt på volum, vi vet allerede radiusen til stjernen vår som er \(R = 2.0086\cdot 10^{6}\ km\), massen er på \(7.9418\cdot 10^{30}\ kg \). Setter vi dette inn i uttrykket for \(\rho\) får vi \(\rho = 233.93\ kg/m^3\).
Vi vet at trykket i en ideell gass kan skrives som
\(P = \dfrac{\rho k T(r)}{\mu m_h}\)
\(k\) er Boltzmann konstanten \(\mu\) er midlere molekylvekt, \(T\) er temperatur, \(m_h\) er massen til et proton og \(\rho\) er massetettheten som vist over. Ok, hva nå? La oss nå se på antagelse nr. 2 og nr. 3, vi kan ignorere strålingstrykk og at stjernen er i hydrostatisk likevekt. Fra videregående lærte du nok at det som gjør at en stjerne ikke kollapser på grunn av sin egen tyngdekraft kommer av det vi kaller for strålingstrykk. Så om vi her antar at strålingstrykket ikke er til stede så må det være en annen kraft som motvirker tyngdekraften. Denne kraften er trykket \(P\) som virker utover. Så vi kan nå inkludere hydrostatisk likevekt, og fra antagelse nr. 3 så kan vi anta at det er hydrostatisk likevekt gjennom hele stjernen.
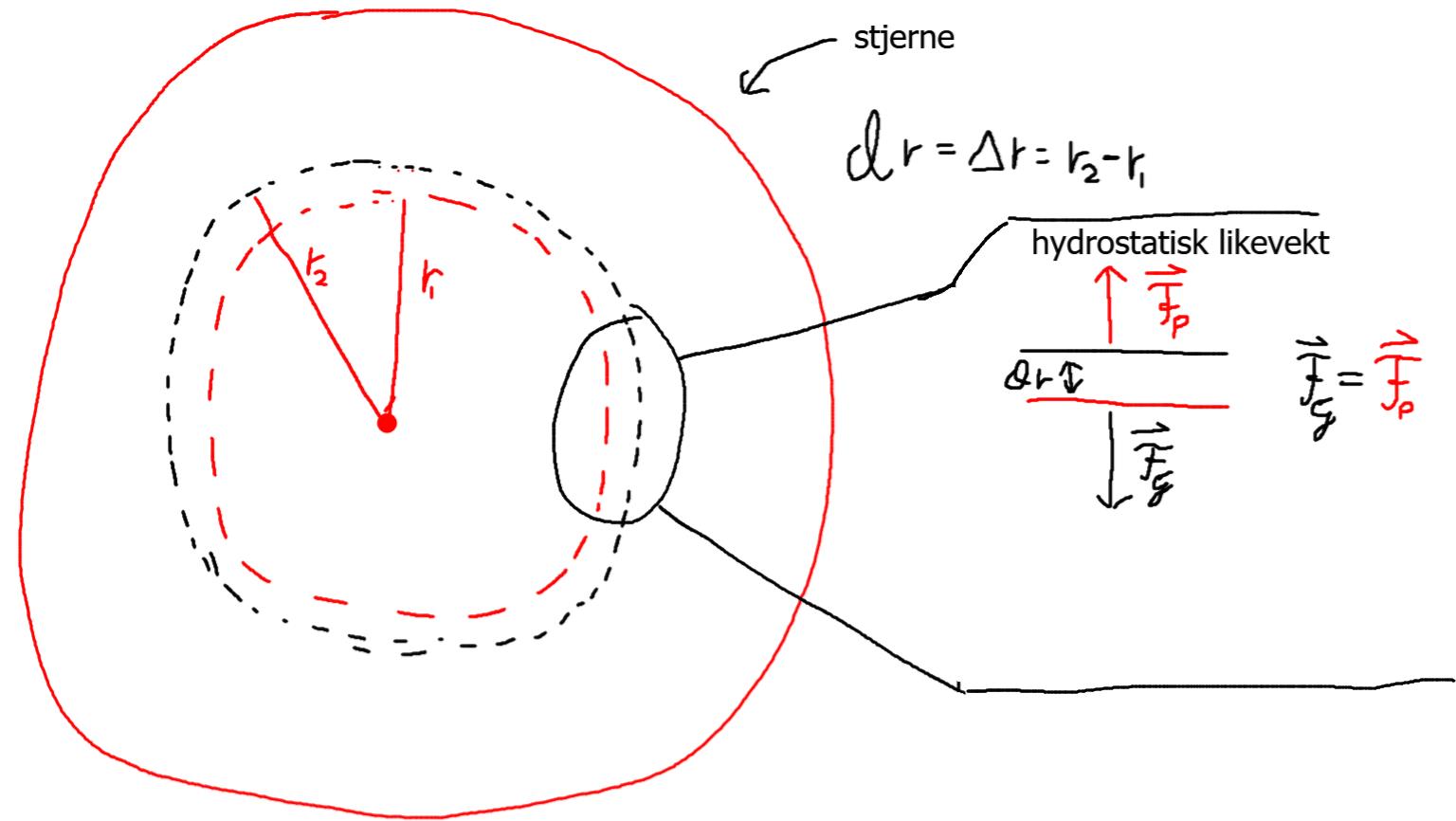
Usikker på hva hydrostatisk likevekt er, så se bildeteksten over. Så fra antagelsen om hydrostatisk likevekt har vi nå mer å jobbe med. Vi kan starte med å finne hvor stor tyngdekraften er i en gitt radius, som ved å bruke newtons gravitasjons lov blir
\(g(r) = G\dfrac{M(r)}{r^2}\) der \(G\) er gravitasjonskonstanten. Likningen for hydrostatisk likevekt er gitt som
\(\dfrac{\partial P}{\partial r} = -\rho g\). \(\partial\) er bare en fancy måte å si at man deriverer. Setter vi disse to uttrykkene sammen får vi
\(\dfrac{\partial P}{\partial r} = -\rho G\dfrac{M(r)}{r^2}\)
Setter vi alt sammen så vil vi få følgende


Grunnen til at vi integrerte fra \(0 \rightarrow R\) er at vi ønsket temperaturen fra kjernen og helt ut til der stjernens overflate. Kjernetemperaturen kan vi nå finne ved å sette inn det vi vet om stjernen vår fra før av. For \(T(R)\) så velger vi overflate temperaturen, \(\mu\) er lik 1, fordi den midlere molekylmassen er den gjennomsnittlige massen til alle molekylene i stjernen. Så på grunn av at vi antar at stjernen bare består av protoner, altså en type molekyl, så vil \(\mu = 1\). \(k\) er en konstant så den kan vi slå opp. Skriver opp verdiene slik at det er lett å holde oversikten.
\(T(R) = 11696.4\ K \\ R = 2.0086\cdot 10^{6}\ km\\ M_h= 1.673 · 10^{−27}\ kg\\ k = 1.38\cdot 10^{-23}\ J/K\\ \rho_0 = 233.93\ kg/m^3\\ \mu = 1 \)
Etter å ha puttet inn verdiene i uttrykket for \(T_c\) får vi at temperaturen i kjernen er på rundt \(T_c = 16\cdot10^6\ K\). Hmm, hadde forventet noe høyere temperatur i kjernen. En av grunnene til at jeg hadde forventet en høyere temperatur er på grunn av massen til stjernen vår. Den er så og si fire ganger så massiv som solen, så det et vi bare har en million kelvin høyere temperatur i kjernen i forhold til solen virker litt urimelig, med tanke på trykket burde være større, en god del større. Om vi husker tilbake til da vil designet rakett motoren vår så var trykket en av faktorene som kunne bidra til at den midlere kinetiske energien til en partikkel økte. Bruker vi samme tankegang her så burde en høyt trykk føre til at temperaturen også øker. Her kan en av våre antagelser, at det er uniform tetthet i hele stjernen være årsaken til at vi får et såpass lav temperatur. Greit nok, la oss gå videre og se om de neste resultatene er i samsvar med hva vi kan forvente, spesielt når vi skal sammenlikne luminositeten med den vi finner gjennom våres veldig forenklede modell.
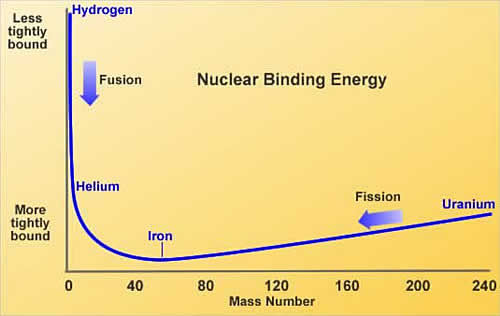
La oss nå se på energiproduksjonen i kjernen for så å prøve å finne luminositeten til stjernen vår. Vi nevnte tidligere at det foregår fusjon i kjernen av en stjerne. Dette er prosessen som står for energiproduksjonen og går på at to molekyler slås sammen, fusjonerer, og danner et tyngre grunnstoff. Dette gir så fra seg energi på grunn av noe som kalles nuklidemasse. Nuklidemasse er massen til en nuklide delt på antall nukleoner. Differansen mellom total nuklidemasse før en reaksjon og etter er det som gjøres om til energi. Hvorfor fusjon og ikke fisjon? Vel, stjerner består av de letteste grunnstoffene, hydrogen, helium etc, andre tyngre grunnstoffer kommer hovedsakelig fra døde stjerner for stjerner produserer tyngre grunnstoffer i løpet av deres levetid gjennom fusjon, til de dør og slipper dem ut.
Luminositet er definert som utstrålt energi delt på tid, du kjenner kanskje igjen denne enheten som watt. Vi er interessert i energi delen i dette, så om vi finner ut av hvor mye energi som kjernen produserer pr tidsenhet så kan vi finne luminositeten. Basert på kjernetemperaturen \(T_c=16\cdot 10^6\ K\) vi fant tidligere kan vi gjøre følgende antagelser.
- All fusjonen skjer innenfor et volumet av en kule med radius \(0.2 R\)
- Vi antar at all energien som blir produsert i kjernen kommer fra pp skjeden og CNO syklusen.
- Vi antar at kjernen består av \(74.5 \)% Hydrogen, \(25.3\)% Helium og \(0.2\)% Karbon, Oksygen og Nitrogen
- Antagelsen om at tettheten er uniform gjelder fremdeles, i tillegg antar vi at temperaturen vi kom fram til \(T_c=16\cdot 10^6\ K\) er lik gjennom hele kjernen.
Alle antagelsene er ganske store antagelser, men kanskje dette gir et resultat som motstrider det vi har observert, og det vi kom fram til som \(T_c\). Den ene antagelsen som står frem som mest urealistisk er at tettheten er uniform. Man kan tenke seg en atmosfære som man faller gjennom. Øverst vill tettheten være lavest, fordi alle luft partiklene ligger oppå alt som er under. Går man til midten av atmosfæren så kan man tenke seg at partiklene i en gitt høyde over bakken både ligger oppå andre partikler men at alt over dytter alt under seg ned, som vil øke tettheten. Helt nederst på bakken har man kun alle partiklene over som presser ned, og dermed tvinger partikler nærmere hverandre som øker tettheten i det område.
Hadde \(T_c > 90\cdot 10^6\ K\) så ville vi ha brukt noe som heter \(3\alpha\) reaksjonen, men på grunn av at det ikke er det, så bruker vi antagelse nr. 2. Så hva er egentlig pp-kjeden og CNO-syklusen? Vi vil starte med pp-kjeden.
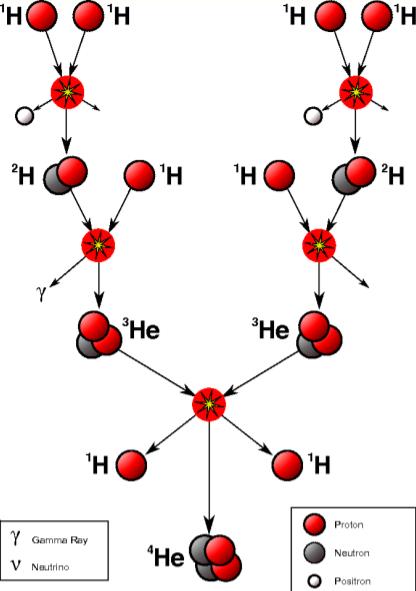
Første reaksjonen vi har i pp-kjeden er to protoner som danner Deterium, inkludert et positron \({^0_0\bar{\mathrm{e}}}\), et elektron \({^0_0\nu_\mathrm{e}}\) og energi. Deretter fusjoneres Deterium med et proton som resulterer i et foton og et isotop av helium \({^3_2\mathrm{He}}\) og energi. Deretter fusjonerer isotope med et annet isotop som resulterer i 2 protoner, Helium og energi. pp-kjeden kan dermed bli skrevet som følgende
\({^1_1\mathrm{H}} + {^1_1\mathrm{H}}\rightarrow {^2_1\mathrm{H}} + {^0_0\bar{\mathrm{e}}} + {^0_0\nu_\mathrm{e}}\)
\({^2_1\mathrm{H}} + {^1_1\mathrm{H}}\rightarrow {^3_2\mathrm{He}} + {^0_0\gamma}\)
\({^3_2\mathrm{He}} + {^3_2\mathrm{He}}\rightarrow {^4_2\mathrm{He}} + 2\times{^1_1\mathrm{H}}\)
Denne reaksjonen er mest effektiv rundt \(15\cdot 10^{6}\ K\).
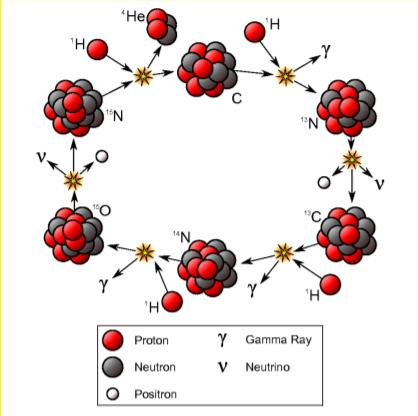
For CNO-syklusen
\({^{12}_6\mathrm{C}}+{^1_1\mathrm{H}\to^{13}_7\mathrm{N}}+{^0_0\gamma}\)
\({^{13}_7\mathrm{N}}\to{^{13}_{6}\mathrm{C}}+{^0_0\bar{e}}+{^0_0v_e}\)
\({^{13}_6\mathrm{C}}+{^1_1\mathrm{H}}\to{^{14}_7\mathrm{N}}+{^0_0\gamma}\)
\({^{14}_7\mathrm{N}}+{^1_1\mathrm{H}}\to{^{15}_8\mathrm{O}}+{^0_0\gamma}\)
\({^{15}_8\mathrm{O}}\to{^{15}_7\mathrm{N}}+{^0_0\bar{e}}+{^0_0v_e}\)
\({^{15}_7\mathrm{N}}+{^1_1\mathrm{H}}\to{^{12}_6\mathrm{C}}+{^4_2\mathrm{He}}\)
Noe som er verdt å merke seg er at mengden av C, O og N ikke går ned fordi de fungerer som katalysatorer for fusjons prosessen. Denne prosessen forekommer i temperaturer rundt \(20\cdot 10^6\ K\) og er følsom for endringer i temperaturen.
Nå er spørsmålet hvordan finner vi ut av energien vi får ut fra fusjons prosessene i kjernen. Den generelle formelen for energien som blir produsert i en fusjonsprosess er gitt som
\(\varepsilon_{AB} = \varepsilon_{0,\mathrm{reac}}X_AX_B\rho^\alpha T^\beta\), her var det en del ukjente tegn. Vi starter med det som er kjent, tettheten \(\rho\), \(\alpha\) og \(\beta\) er avhengig av temperaturen, og \(X\) er prosentandelen av et grunnstoff som den totale massen vi ser på består av. For oss vil dette være \(X_H=0.745\), \(X_{He}=0.253\) og for \(X_{CNO} = 0.002\). For oss vil \(\varepsilon_{0,\mathrm{reac}}\) bli oppgitt for en gitt prosess.
Vi kan starte med å se på pp-kjeden. Energien fra pp-kjeden kan bli skrevet som
\(\varepsilon_\mathrm{pp} \approx \varepsilon_{0,\mathrm{pp}}X_H^2\rho T_6^4\)
hvor \(\varepsilon_{0,\mathrm{pp}} = 1.08\cdot10^{-12}\;\mathrm{Wm^3/kg^2}\) og \(T_6\) er temperaturen i millioner kelvin. For vårt tilfelle så blir \(T_6^4 = 16^4\ K\). Verdien vi får for \(\varepsilon_\mathrm{pp} = 9.1897\cdot 10^{-6}\ W/kg\). Gjør det samme CNO-skjeden der energien fra denne prosessen kan skrives som
\(\varepsilon_\mathrm{CNO} = \varepsilon_{0,\mathrm{CNO}}X_HX_{\mathrm{CNO}}\rho T_6^{20}\)
Her er \(\varepsilon_{0,\mathrm{CNO}} = 8.24\cdot10^{-31}\;\mathrm{Wm^3/kg^2}\), og \(T_6^{20} = 16^{20}\ K\). Setter vi inn verdiene får vi at \(\varepsilon_\mathrm{CNO} = 3.4722\cdot 10^{-7}\ W/kg\)
Sammenhengen mellom luminositet og energien vi fant kan bli uttrykket som
\(\dfrac{dL(r)}{dr} = 4\pi r^2\rho(r)\varepsilon(r)\), der \(\varepsilon(r) = (\varepsilon_\mathrm{pp} + \varepsilon_\mathrm{CNO}) \), og \(\rho = \rho_0\). Her integrerer vi på begge sider fra \(0 \rightarrow 0.2R\) og da får vi
\(L = \dfrac{4\pi}{3}\rho_0(\varepsilon_\mathrm{pp} + \varepsilon_\mathrm{CNO}) \cdot \left[ r^3\right]_{0}^{0.2R}\)
\(L = \dfrac{4\pi}{3}\rho_0(\varepsilon_\mathrm{pp} + \varepsilon_\mathrm{CNO}) (0.2R)^3\)
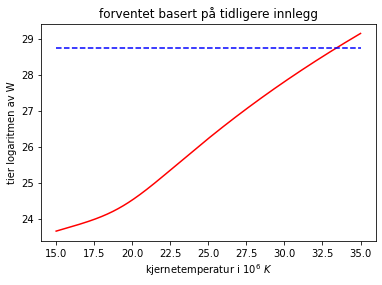
Setter vi inn verdiene og regner ut får vi \(L = 6.06\cdot 10^{23}\ W\), et høyt tall, men hva sier det i forhold til luminositeten vi fant i forrige innlegg. Luminositeten vi fant der var på \(L_s = 5.3804347\cdot10^{28} \mathrm{W}\), ser vi nå på forholdet \(\dfrac{L}{L_s} = 1.1\cdot 10^{-5}\) ganger mindre i forhold til det vi fant tidligere. En av disse er definitivt feil, og sjansen for at det er luminositeten vi fant her som er feil er ganske stor med tanke på alle antagelsene og forenklingene vi gjorde på veien. Det som mest sannsynlig hadde størst effekt var nok tettheten. Som nevnt tidligere så kan man ikke forvente at tettheten er uniform og lik i hele stjernen. Tettheten og trykket vil øke desto nærmere sentrum man kommer, og dermed også temperaturen.
Slår man opp på den type stjerne vi har, en type B i hovedserien, så finner man at først at energien kommer hovedsakelig fra CNO-syklusen, som krever temperaturer på rundt \(T = 15\cdot 10^{6}\ K\) på å starte, og rundt \(T = 17\cdot 10^{6}\ K\) er det den dominerende kilden til energi. Det står også at type B stjerner ikke har en konveksjonsstrøm i seg, slik solen har. Ta dette med en klype salt, men om jeg ikke husker feil, så er konveksjon en av de beste måtene å transportere varme på. Mangel på dette gjør at temperaturen i stjernens indre har det mye vanskeligere å slippe ut, og dermed vil temperaturen bli bevart i langt større grad enn om det hadde hatt konveksjon.
Den andre antagelsen som kan ha ført til at resultatet var så forskjellig er at vi antok at all fusjonen foregikk innenfor en kule med radius på \(0.2R\). Vår stjerne sin energiproduksjon er konsentrert i sentrum av kjernen, som danner konveksjonsstrømmer rundt kjernen, som bringer hydrogen inn der fusjonen foregår. Denne konsentrasjonen av fusjons prosesser, mangel på god varmetransport eller overføring av varme, og høye tettheten gir oss grunn til å tro at resultatet er for lavt, og burde ha vært høyere. Siste tingen som støtter dette er at vi er under \(T = 17\cdot 10^{6}\ K\)dersom vi antar at den dominerende kilden til energi skulle ha vært CNO-syklusen så er dette et ganske tydelig tegn på at vi har for lav temperatur.
Av ren nysgjerrighet plottet vi dette for å se hva som skulle til for å få tilsvarende resultat med den tidligere innlegget. Verdt å nevne er at det kan hende begge er feil, og at luminositeten vi fant tidligere er for høy. Det betyr heller ikke at begge kan være feil, men basert på informasjonen vi har nå, så er det mye som tyder på at temperaturen i kjernen er for lav. Med hvor mye er vanskelig å si, alt vi vet, er at den burde ha vært høyere.