You may have heard of this little thing in relativity called the twin paradox? The scenario where you send one twin off in a rocket to a distant planet and back at near lightspeed and see who is the oldest twin upon the return. Well, today we're going to look at this exact problem with two fine ladies; Lisa and Maggie. They live on a planet called Homie, but Lisa yearns for an interstellar journey to a planet known as Destiny, which is a whopping 200 lightyears away.
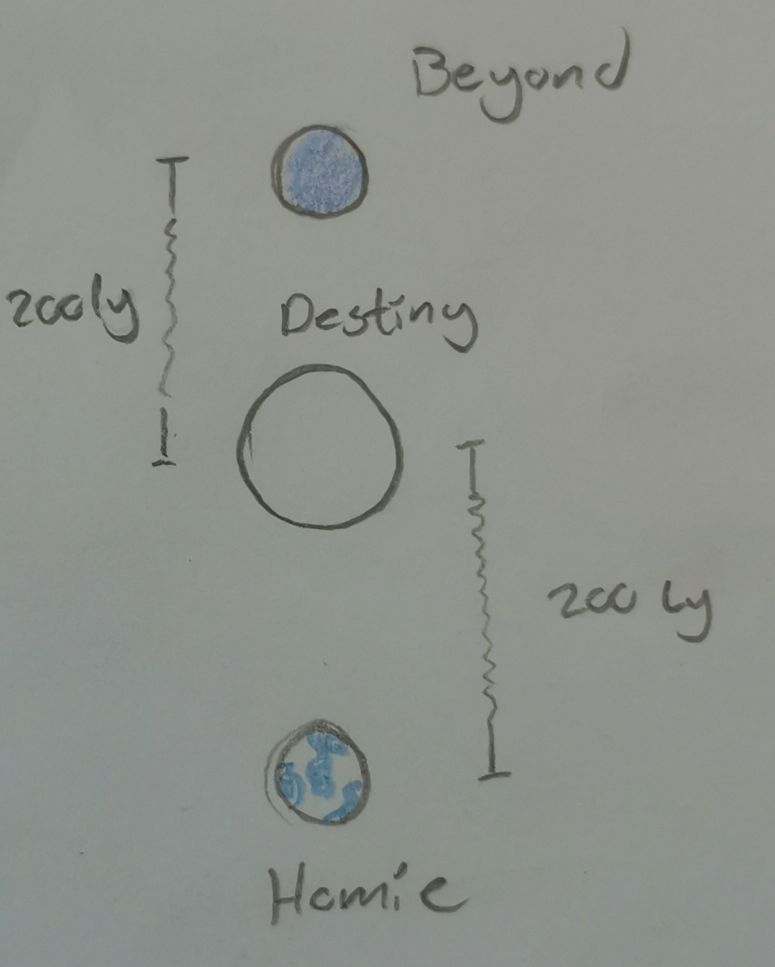
Lisa intends to get there quickly, so she boards a craft which can travel at 99% the speed of light or 0.99c! Yet even at this insane speed she should spend around 202 years getting there right? (we find this from distance/velocity) She can't exactly move faster than the speed of light, and the planet is 200 light years away so there's no way she could get there faster, right? Well for Maggie, Lisa would spend 202 years travelling form Homie to Destiny, however, if we change our frame of reference to Lisas, we suddenly have a very high velocity. Thus we need to utilize lorentz transformations for time, since, as we know from special relativity, spacetime starts behaving differently at higher velocities. We'll be using the lorentz transformation for time in this case as this is the variable of interest: \(\Delta t = \gamma\Delta t'=\frac{\Delta t'}{\sqrt{1-v^2}} => \Delta t \sqrt{1-v^2} = \Delta t'\) (where \(\Delta t\) is Magies experienced time on Homie and \(\Delta t'\) is Lisas experienced time aboard the spacecraft, though you may be used to seeing v2 written as \(\frac{v^2}{c^2}\), which is also correct, but we're using relativisic numbers, meaning c = 1 for us), this gives us that Lisa spends as little as 28.5 years on her journey in her own frame of reference. Which to reitterate from earlier, alligns with what we know about special relativity; an observer at rest will experience time faster than an observer with a higher constant velocity. During her trip to Destiny, however, Lisa became incredibly homesick, so upon her arrival she immediately turns around and returns to Homie. On the way back, let's assume Lisas frame of reference as our baseline, it really shouldn't change anything, cause if we treat Lisa as if she were at rest the planets will suddenly be the things moving, there should be no differene right? What is stationary is relative after all. Plopping in the same formula with 28.5 years as \(\Delta t\) this time, we get that the time Lisa spends on her way back to Homie is a mere 4 years for Maggie. Wait, 4 years?! That can't possibly be right, if it were she would need to travel more than 50 times the speed of light, but this isn't the biggest issue. This means the trip takes both 8 years and 404 years in the same frame of reference depending on if we assume its at rest or not, this is wrog, it has to take the same amount of time in the same frame of reference, something is amiss here. So let's go back and see if we've made any incorrect assumptions along the way.


So we assumed the change of reference was equal in both scenarios, right? But is it really? If both frames were moving at constant velocity compared to eachother, this would be the case. But do we actually have constant velocity here? Well what happens when the space ship turns? That's right, it changes the direction of the velocity, meaning it's accelerating for a tiny amount of time, but this is enough to invalidate lorentz transformations from special relativity. This is because special relativity only applies when we have constant velocity, as soon as we have assceleration, or an accelerated field it falls apart. However, we can still use a symetry argument here right? Cause in the frame of reference of Lisa the planets are also changing dirction, while technically correct there is a slight detail which rules out this symetry argument; the difference is in the fictional force experienced during the acceleration. This simly does not occur in the planets frame, but it does for Lisa in the rocket. In other words something happens during the acceleration leading to some funky timey wimey shenanigans.
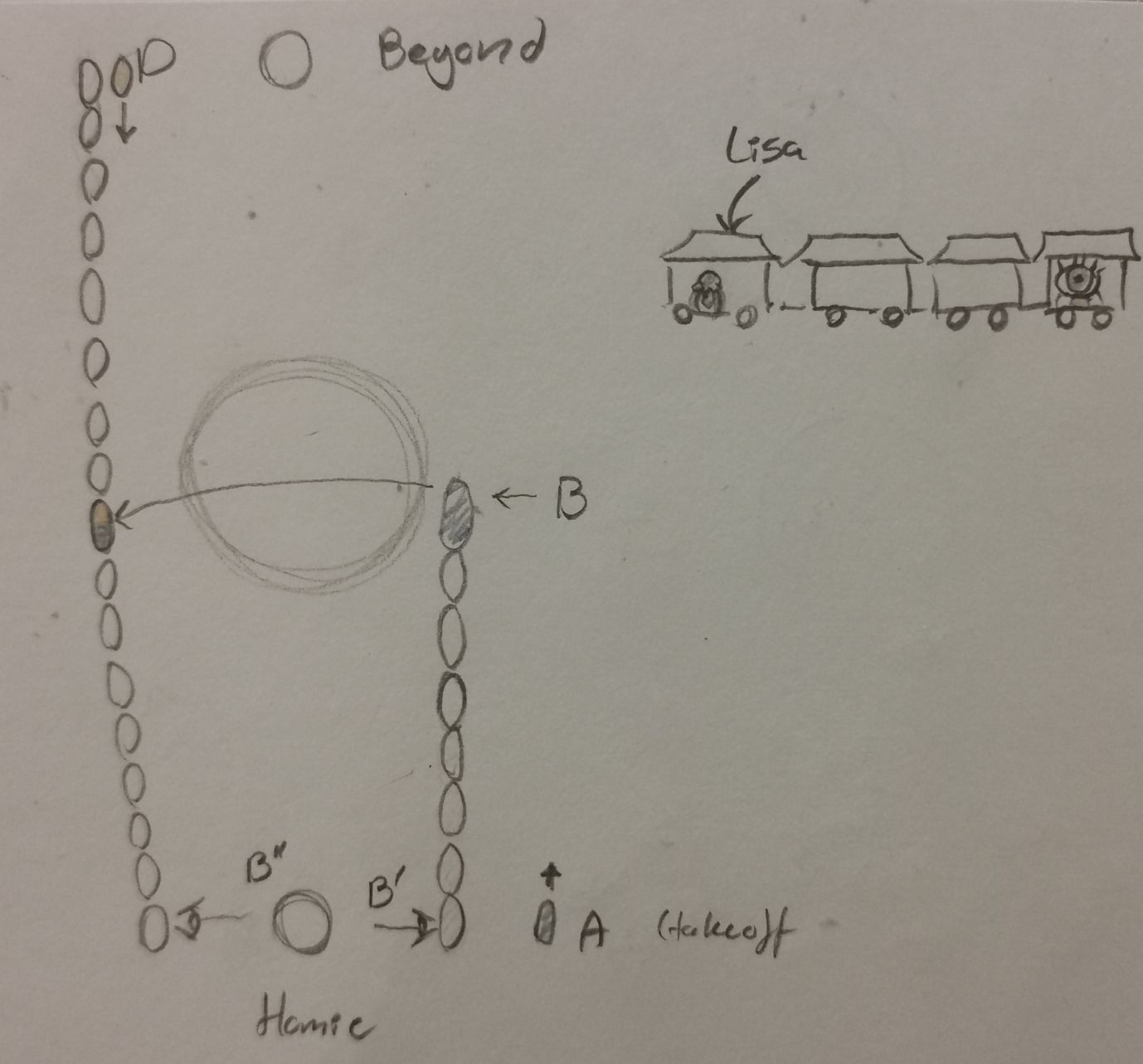
To explore this more thoroughly we're going to introduce a few things into our system. Firstly we'll introduce a new planet, named Beyond, 200 lightyears beyond Destiny, a new traveller named Peter, who travels from Beyond to Homie via Destiny at a velocity of 0.99c (the same as Lisa) and, lastly, we give each of the rockets a train of rockets connected to eachother in front of- and behind Lisa and Peter, as if they were carts in a long train of rockets. Next we're going to define a few events, (something called events, which are simply coordinates in spacetime, so an example of this is) the first of which, event A, is the rocket taking off from Homie, which will occur at t = 0, and x = 0 in both the Homie-, and rocket system. Cause the rocket is at Homie, and the time hasn't started passing yet. We'll define an event D, which is Peter taking off from Beyond, which also occurs in t = 0, but the position will vary depending on our frame of reference here. For notation reasons we'll define L0 as 200ly (light years), the planets system as unmarked (xB, tB etc.), Lisa's as marked (t'B and x'B) and Peters as double marked (t''B and x''B). So for event D x and x' = \(2L_0\) and x'' = 0. Now we want to look at how an observer in one of these rocket train carts will observe the time passing on Homie. And to do this we'll introduce an event B, being when Lisa arrives at Destiny. We're also introducing two related events: B' and B''; Similtaneously with Lisas arrival at Destiny a flash of light is sent out from the rocket right next to Homie at the time, this event will be called B' and during this time the observer in aformentioned cart will look at the passage of time in Homies clocks. Similarly, at event B'' the observer in Peters train (who is ahead of Peter) observes the passed time at Homie, but this flash of light occusr after lisa has jumped from her own ship to Peters.
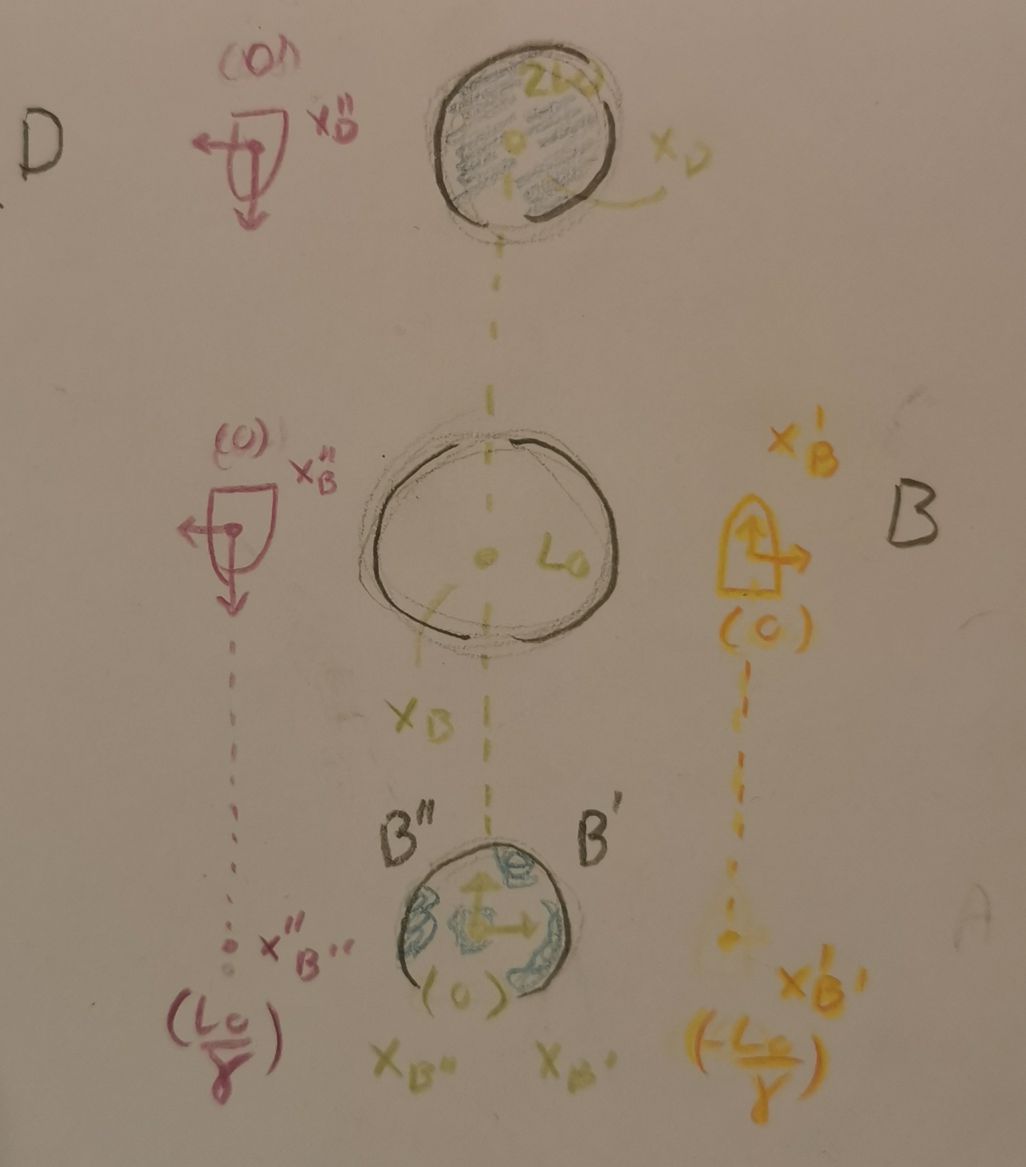
We wish to find the times the observers in Lisa's and Peter's systems observe on Homies clocks, in other words the time passed on Homies frame of reference during event B, which should tell us the effect switching frames of reference has. The times we wish to find are denoted as tB' and tB'', there are a few things to cover here so let's take it one step at a time. Let's start off by finding tB'; the time passed on Homie as seen by the observer in Lisas system/rocket train. To find this we'll need two formulas: \(t'_{B} = -v\gamma x_{B}+\gamma t_{B} \space (1)\) and \(t_{B'} = -v\gamma x'_{B'} + \gamma t'_{B'} \space (2)\). So this is now a problem of finding four varables; xB, tB, x'B' and t'B', luckily these aren't difficult to find. Let's start off with the simple ones: xB and tB. Since these are in Homies frame of reference, we have no time or lenght contraction, so xB is simply L0 and tB = \(\frac{L_0}{v}\). We can then proceed to find t'B using these and the formula above (1). We are now in Lisas frame of reference, something we can use to our advantage. You see in Lisa's frame of reference tB and tB' occur similtaniously. So we can set these equal to eachother, and you may now see where we go next? We'll first set \(t'_B = -v\gamma L_0 + \gamma L_0 = L_0\gamma(\frac{1}{v}-v) = \frac{L_0\gamma}{v}(1-v^2) = \frac{L_0\gamma}{\gamma^2v} = \frac{L_0}{\gamma v} = t'_{B'} \). We can still use Lorentz transformations here, as this is pre change in direction, and the velocity is constant. Now x'B' is fairly simple to find: \(x'_{B'} = -v t'_{B'} = -v \frac{L_0}{\gamma v} = - \frac{L_0}{\gamma}\) (it is negative as it occurs behind event B in th spacial dimention here (x'B is in the origin)). We're able to use this in both cases due to having an origin event, so we know the only factor contributing to differing time and position would be contractions due to special relativity. Using formula (2) we now find \(t_{B'} = v\gamma(\frac{-L_0}{\gamma}) + \gamma(\frac{L_0}{\gamma v}) = \frac{L_0}{v} - vL_0 \approx 4yrs\).

Meaning event B' occurs only 4 years after Lisas departure as we found earlier! But she still takes 404 years on the round trip in the Homie frame of reference, what's up with that? To solve this, let's see what happens when we view this in the same frame as the observer at the front of Peters 'train' at event B''.
Here xD = 2L0 as the starting position for Peter is at Beyond (which is 2L0 away). x'' = 0 at all times as the position of the rocket is where Peter is a any given time, the starting time tD = t''D = 0. We have to get a bit creative here, as we don't have an origin event (where x and t are 0 in all frames of reference), thusly we can't immediately use lorentzian transformations. We need to show the system bahaving similarly to Lisas first then if it does we can use lorentzian using a symetry argument. So instead we opt to use change in position and time in each system as the velocity is, luckily, constant within Peters frame of reference. So we try to find: \(\Delta x_{BD} = x_D-x_B\), \(\Delta t_{BD}=t_D-t_B\), \(\Delta x''_{BD}=x''_D-x''_B\) and \(\Delta t''_{BD} = t''_D - t''_B\). Which equals \(2L_0-L_0 = L_0\), \(0 -202yrs = -202yrs\), \(0 - 0 = 0\) and \(0 - (-v\gamma x_B + \gamma t_B) = \frac{-L_0}{\gamma} \text{(Similarly to $t'_{B'}$ from earlier, but it occurs before event B)}\) respectively. This is, as briefly mentioned, simply to show that Peters system behaves similarly to Lisas, when it's at Destiny. Thus we can use symetry and assume t'B and t''B are the same as the spaceships both travel at the same velocity and for the same distance, they're just pointing in different directions. To find tB'' we'll be using the same method as we did to find tB' meaning we need \(x''_{B''}=\frac{L_0}{\gamma}\) and \(t''_{B''}=t'_B = \frac{L_0}{\gamma v}\). When we put this into the formula (2) we get: \(t_{B''} = v\gamma \frac{L_0}{\gamma} + \gamma \frac{L_0}{\gamma v} = vL_0 + \frac{L_0}{v} = 400yrs\). Woah, that means the clocks on Homie speed forward 396 years during Lisas change in frame of reference!
Now, lastly, let's look a bit at this acceleration to see exactly how much older Lisa will be than Maggie once she returns to Homie. Firstly we make Peter un-exist, Lisas rocket is all we care about, for the moment. We also need a more concrete number for our acceleration, as 'Lisa turns around during the event' can be slightly arbitrary to work with, so let's give her rocket an acceleration of \(g = -0.1\frac{m}{s^2}\), (meanig it's deaccelerating). First off we wish to find how long it takes for the rocket to come to a complete halt, where v = 0, we'll call this point TP. In Homies frame of reference, our first step is going to be to split the journey in two; the constant velocity phase between Homie and Destiny, and the deacceleration phase, between Destiny and TP. The first of the two is simple to find; we know tA=0, and we know tB. Since both v and g are constant we can use newtons laws of motion to find TP by: \(TP=> v= 0 = v_0 + gt_B\), which we can fiddle a bit with in order to get: \(TP = t_B - \frac{v_0}g\). But how does time on Homie pass compared to that of the rocket during the accelerated phase? To find this, we'll need to look at the time in the rocket as opposed to on Homie, in the rockets frame of reference to do this we'll define events Y and Y' which are equivalent to B and B'. Although we can't tell the times exactly, we can tell the positions, we won't goo too much into the calculations, just know that: \(x_{y'} = 0, \ x'_y = 0\) as well as: \(x_y = L_0 + v_0(t-t_b) + \frac{1}2g(t-t_b)^2 \ , \ x'_{y'} = \frac{-x_y}{\gamma (t_y)}\). We can't exactly use newtonian laws of motion to find the time from here, however we can use spacetime distance: \(\Delta S^2 = \Delta t^2 - \Delta x^2\).
The reason this is useful is, we know it is the same in any frame of reference, so since we know the x in both frames of reference we can find the times through this. Giving us: \(t_{y'} = t_y - vL_0 + vv_0(t_y-t_B)+\frac{1}2g(t_y-t_B)^2\). This involves us making a slightly simplified model of the acceleration, which allows us to looks at the velocity in every frame (elevator) from v = 0 to v = 0.99c, with a bunch of frames of reference lined up next to eachother with slightly changing velocities, kinda like Lisa was jumping over from one elevator to the next until she is able to regain her initial velocity of 0.99c. Additionally we can't simply plop in g here for the acceleration, as both our velocity and distance measurments are relativistic, this means we'll need to make g relativistic as well. Note the relativistic unit for acceleration is \(\frac{1}s\), as velocity has no unit in relativity. To get this we convert every unit into seconds and preform the following: \(g(nat, s) = \frac{\frac{\Delta x}c(SI)}{\Delta t(SI)^2} = \frac1 c \frac{\Delta x(SI)}{\Delta t(SI)^2}= \frac{\Delta x(sec)}{\Delta t^2(sec)}\). Next we can simulate this by using a numerical method such as EulerChromer, as this updates the velocity based on the acceleration over small timesteps (or elevators in our case), although we'll only really be interested in the change in velocity here. Since we assumed symetry earlier we'll just need to look at this in one direction, so we look at the aceleration phase, from v = 0 to v = 0.99c and deduct that it acts the same the other way too. With this we can start looking at the relationship between the times.
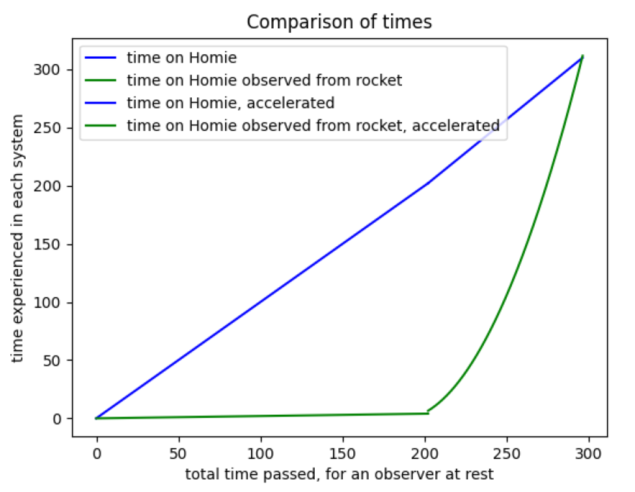
What actually happens with the time in the turning point? Some of you may have already seen it, but since the velocity is 0 here, both the planets and the rocket are in the same frame of reference, meaning tY = tY'. We can claim this since we know t'Y = t'Y' in the rocket frame of reference, so since they're now in the same frame of the reference we know all the events happen similtaniously in the turning point. Thus one way the graph will look something like the graph on the left. Though the time on Homie should be more linear, unlike what is depicted. What is important to note is that a substantially larger portion of time passes on Homie before event B while for the rocket the overwhelming majority will pass after event B, meaning the clocks on Homie seen from the rockets have to speed up a lot. The two plots under have their x- and y-axis switched compared to the illustrated above. Although they're not accurate to what we'd expect to see, partially due to a failed impementation of the numerical method, it seems the main cause of this has to do with the conversion of g into relativistic units, which meand we have to execute multiple operations on it to get our desired formula, this, however seems to either cause comfusion on the simulations, or our part. Despite their shorcomings, the plots do reflect the phenomena we expect to find! As discussed above; the time on Homie doesn't speed up it remains constant, while observed from the rocket it speeds up substantially once it starts decellerating. Which will lead to the clocks alligning, although we'll see that the experienced time for Lisa remains different from the time an observer in her system observes on Homie.
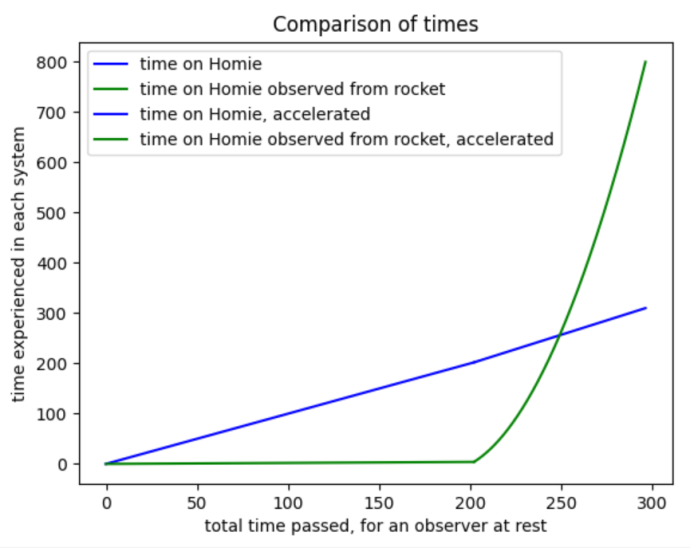
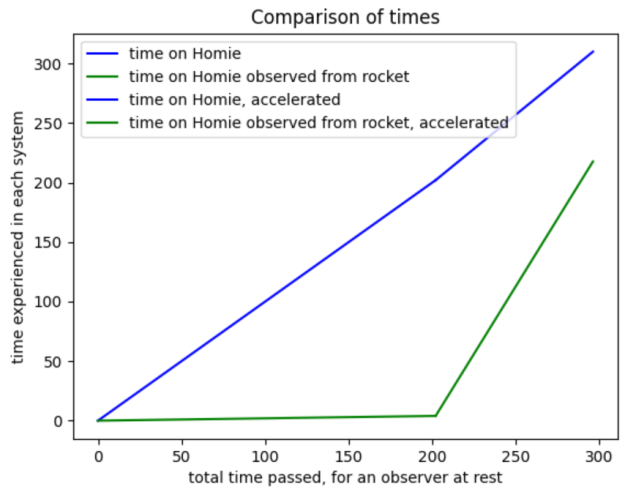

The time passed on Homie from the ships frame of reference in the constant velocity phase, as we mentioned, is 4 years. Then during the acceleration the time starts passing way more rapidly and for the rocket the deacceleration takes 292 years. In Homies frame of reference the same intervals take 202 and 94 years respectively. A pretty identical process will happen when the rocket starts accelerating again, because of this we can argue the processes are symetrical, and thus the time passed on the way to TP is equal to the time passed between TP and Homie. Because of this we can simply double the time of the one-way trip: (2(4+292)years = 2(202+94)years = 592 years). Now the systems finally have the same amount of time pass on Homie, meaning they can be interchanged, and we've found the answer to the paradox. We can now look at how much Lisa actually ages on the round trip! The time passed for Lisa will be 28.5 years during the constant velocity phase, as we found earlier, and 74.6 years during the acceleration, which I won't bother you with the nitty gritty of. This results in a journey lasting 206 years. So Lisa ages less than Maggie. Although she will be a very old Jelly once she returns back hom(i)e.
To summarise, to find the relation between time on Homie as opposed to the observed one, we first found an expression for each possition of the rocket ship compared to Homie, in other words the distance between the two at any given point during the accelerated phase. With this we could use the spacetime distance to find the relationship between the times, however thse required us to know the velocity at any given position. Thus we had to find the acceleration of the rocket, we did this by introducing a simplified model for the acceleration; an elevator model, where Lisa jumped from one elevator to the other, where the elevators worked as a series of frames of reference. Next we converted g into relativistic units so that we could actually work it in to our formulas with otherwise only relativistic units (like L0 and v), and lastly we solved the change in velocity, and time numerically. Ultimately we found that Lisa aged 206 years, and Maggie would have aged 592 years. So Lisa has some catching up to do in the birthday department. We could finally find this difference in aging due to the time on Homie and the time on Homie observed from Lisas frame of reference were the same as one and other once Lisa arrived back at Homie.
