Previously we talked about special relativity (even though it was not mentioned explicitly). In this post we will introduce general relativity! We are going to do that by studying a laser beam, more specifically study the relation between observed wavelength (of the laser beam) from a shell observer and far-away observer.
Do they observe the same wavelength? Or will different wavelengths be observed? If they are different, what is the ratio between the wavelengths? All these questions will be debunked.
Before we do so, there are some things needed to be learned and tools to be accumulated.
Theory section
The key difference between special and general relativity is acceleration. In special relativity we study objects moving with a constant velocity, without influence from external forces. In general relativity the force of gravity is at play, meaning the objects would not move with a constant velocity. They accelerate with gravitational acceleration. However, GRAVITY IS NOT A FORCE (Note: in general relativity it is not a force). The force of gravity is simply a result of curvature in spacetime due to mass (also referred to as spacetime geometry)1.
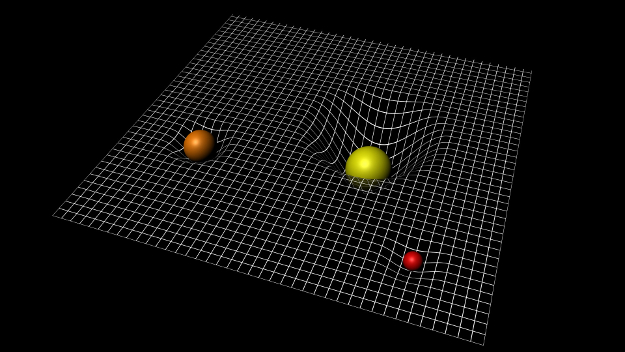
Retrieved from https://cdn.sci.esa.int/documents/34614/35502/1567215794430-ESA_LISA-Pathfinder_spacetime_curvature_above_625x352.jpg
What is spacetime geometry?
Firstly we need to introduce 3 types of geometries in order to explain spacetime geometry.
Euclidean geometry: What I would call "normal geometry". It is what you are used to, where the shortest path from A to B is a straight line (3D)
Lorentz geometry: Quite the opposite of Euclidean where the LONGEST path from A to B is the straight line (4D).
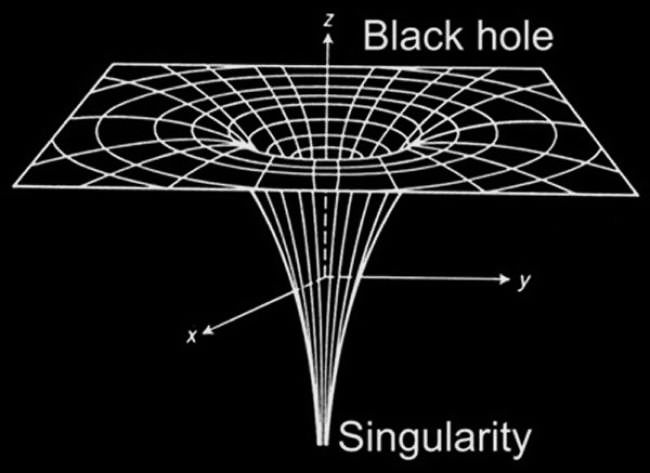
Schwarzschild geometry: Describes the gravitational field around a spherical mass. Valid around a lonely star, planet or black hole.
Warning: I might misspell Schwarzschild a couple times throughout this post... I am not good with spelling...
Back to what is spacetime geometry? The different geometries are specified by a spacetime interval/ line element \(\Delta{s}\). It describes how distances are measured.
You would probably have used a ruler to measure distance, correct? Now, imagine all the three types of geometries have their own unique ruler to measure distance. That is what spacetime geometry is, a description of the different distance rulers.
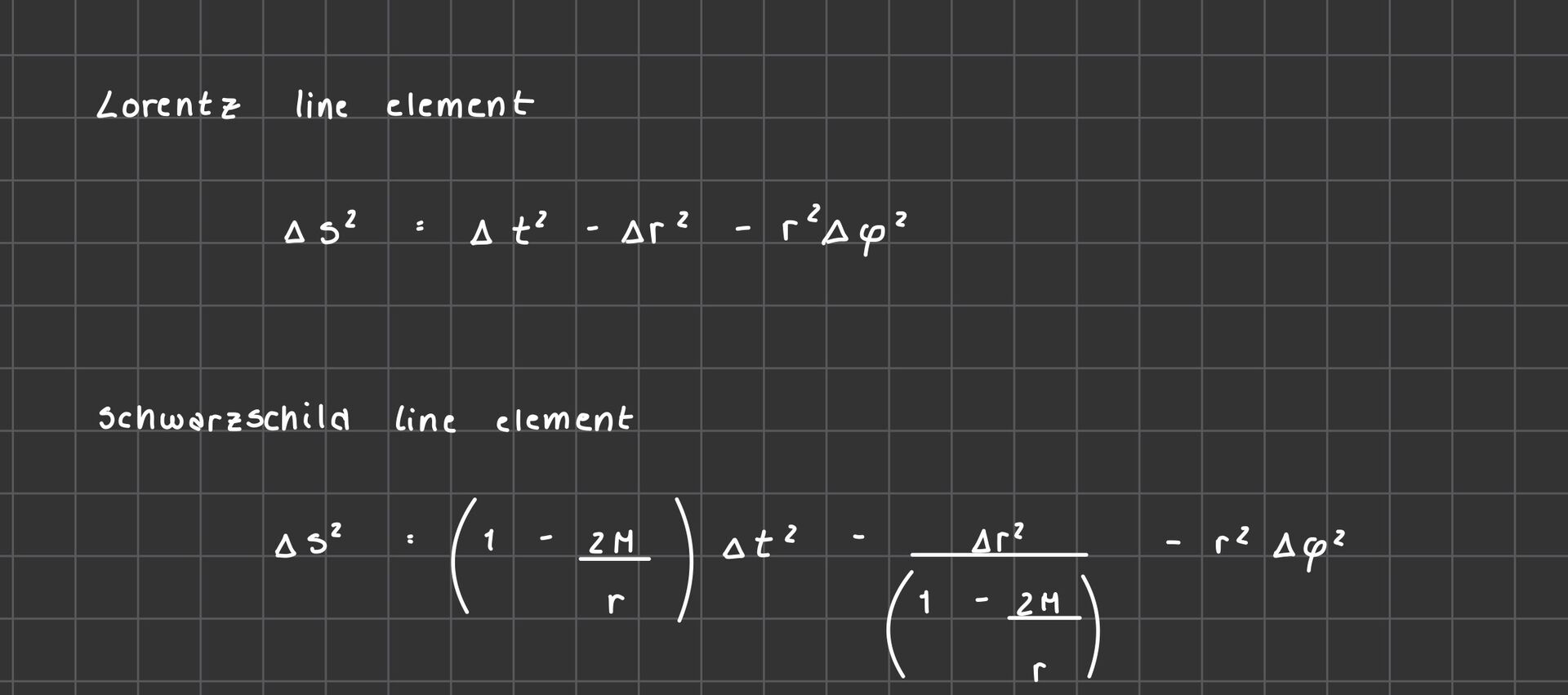
where
M: mass of the spherical object
r: radius of spherical object
Don't get too caught up in details of the line element. Feel free to read about it if you are interested. Otherwise, it is enough if you understand that line element describes how distances are measured.
Now, what is the best way to actually absorb and learn new information? Use the information! Note, I have not written about every detail in the theory section yet. I find it very boring to learn a lot first and then use it. I would have probably forgotten half of it before even reading the exercises. So I decided to only go through the basics and rather mention details throughout the example as need.
So we shall take a look at an example.
1st example (and only example)
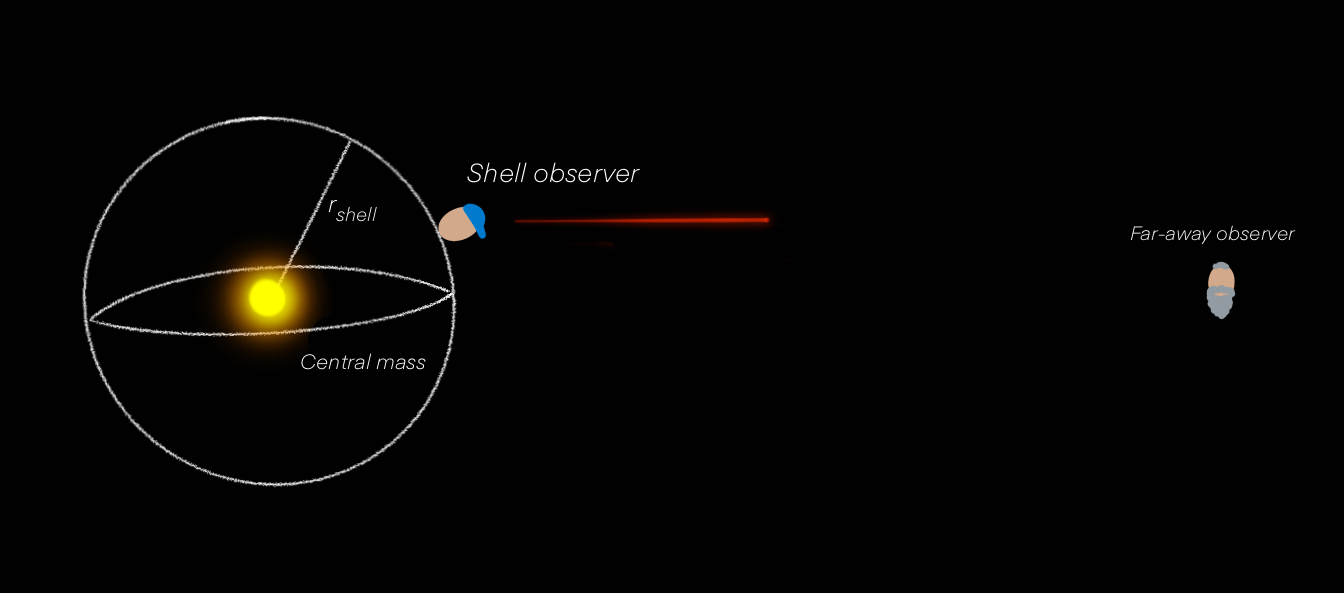
A shell observer on shell in a distance rshell from central mass point a laser pen radially outwards from the central mass. The emitted beam has wavelength \(\lambda = \lambda_{shell}\) and frequency \(\nu_{shell}= \frac{1}{\Delta_{shell}}\). The frequency of the light received by far-away observer is \(\nu = \frac{1}{\Delta{t}}\).
What are we interested in?
We are interested in the wavelength \(\lambda\) observed by far away observer. We already know the wavelength observed by shell observer is \(\mathbf{\lambda_{shell}}\).
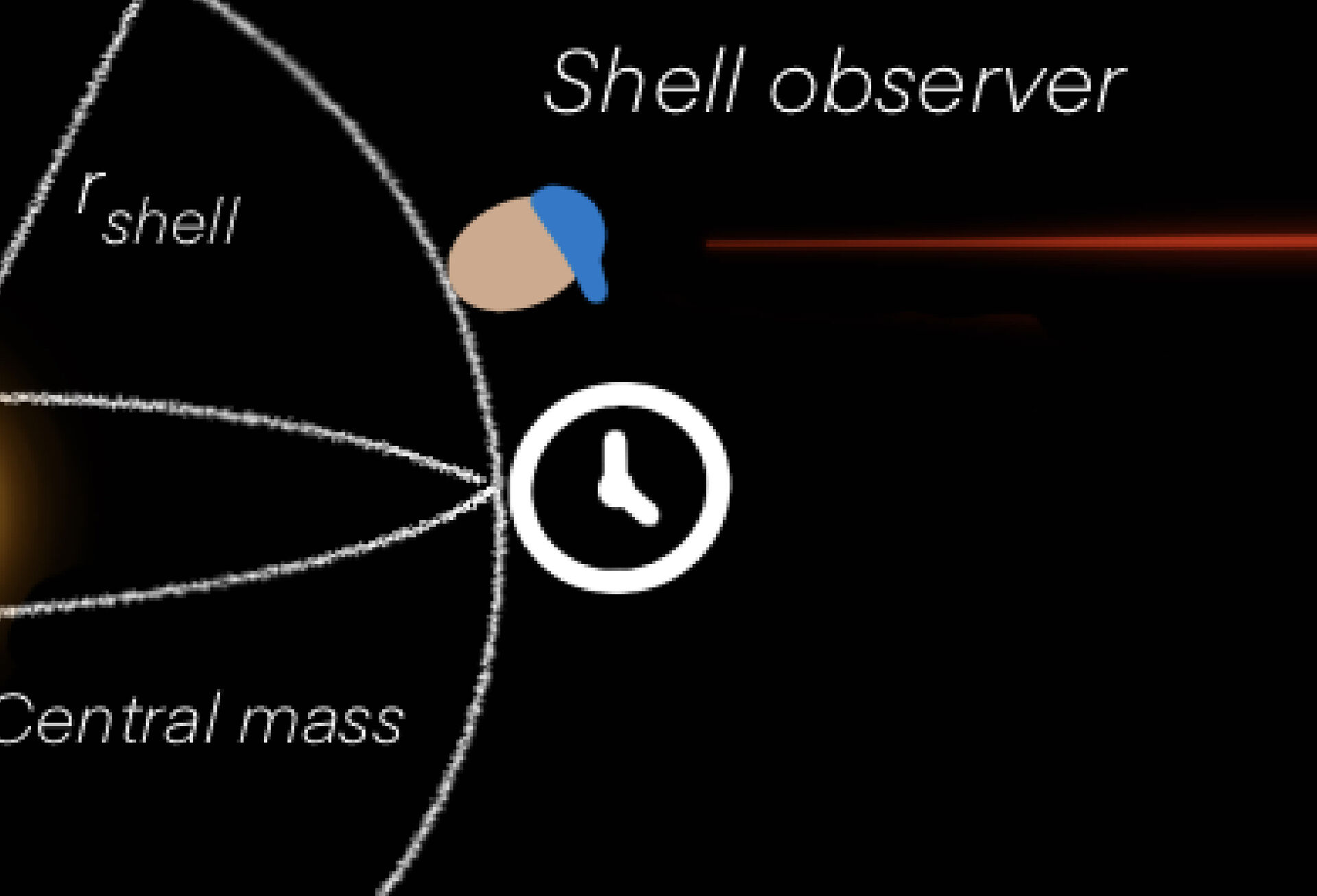
Imagine there is a clock situated on shell rshell which ticks at each time a peak of electromagnetic wave passes. There are two ticks, one at time \(\Delta{t_{shell}}\)(shell observer) and one \(\Delta{t}\) (far-away observer).
Geometry of the different observers.:
Shell observer uses Lorentz coordinates. Line element:\(\Delta{s_{shell}}^2 = \Delta{t_{sh}}^2 - \Delta{r_{sh}}^2-r_{sh}^2\Delta{\phi_{sh}} \tag{1}\)
rsh: distance from central mass to shell
sh = shell
Far-away observer uses Schwarzschild coordinates. Line element: \(\Delta{s}^2 = \left(1-\frac{2M}{r}\right) \Delta{t}^2- \frac{\Delta{r}^2}{\left(1-\frac{2M}{r}\right)}-r^2\Delta{\phi}^2 \tag{2}\)
M: Mass of the object. In this case the object is a black hole.
r: distance from central mass to far-away observer which is really fucking far away.
Detail 1:
Spacetime interval/ line element \(\Delta{s}\) is invariant when relating time and space coordinates in different frames.
By using the detail 1, we can find the difference in time interval measured by the two observes
\(\Delta{s}^2 = \Delta{s_{shell}^2} \tag{3}\)
Insert equation (1) and (2) into (3)
\(\left(1-\frac{2M}{r}\right) \Delta{t}^2- \frac{\Delta{r}^2}{\left(1-\frac{2M}{r}\right)}-r^2\Delta{\phi}^2 = \Delta{t_{sh}}^2 - \Delta{r_{sh}}^2-r_{sh}^2\Delta{\phi_{sh}}\)
The clock is situated at the same position for both ticks, \(\Delta{\phi} = \Delta{r} = 0\). Position coordinates remains the same, thus only a difference in time dimension.
\(\left(1-\frac{2M}{r}\right) \Delta{t}^2= \Delta{t_{sh}}^2 \)
Difference in time interval is given by
\(\underline{\underline{\Delta{t} = \frac{\Delta{t_{sh}}}{\sqrt{\left(1-\frac{2M}{r}\right)}}}} \tag{4}\)
With this fact we can find an expression for \(\frac{\Delta{\lambda}}{\lambda_{shell}}\), gravitational "Doppler" formula. This gives us the wavelength observed by far-away observer for light emitted close to central mass.
\(\frac{\Delta{\lambda}}{\lambda_{shell}} = \frac{\lambda - \lambda_{shell}}{\lambda_{shell}} \tag{5}\)
Detail 2:
Frequency and wavelength are inversely proportional to each other.
\(\mathbf{\nu = \frac{c}{\lambda}}\) Equation for frequency
\(\mathbf{\lambda = \frac{1}{\nu}}\) (Relativistic units: c = 1)
c: speed of light
\(\mathbf{\nu:}\) velocity of light
\(\lambda_{sh} = \frac{1}{\nu} = \frac{1}{\frac{1}{\Delta{t_{sh}}}} = \Delta{t_{sh}} \tag{6}\)
\(\lambda = \frac{1}{\nu}= \frac{1}{\frac{1}{\Delta{t}}} = \Delta{t} \tag{7}\), the expression for \(\Delta{t}\) can be found in equation (4)
Insert equation (6) and (7) into equation (5)
\(\frac{\Delta{\lambda}}{\lambda_{shell}} = \frac{\lambda - \lambda_{shell}}{\lambda_{shell}} = \frac{\frac{\Delta{t_{sh}}}{\sqrt{\left(1-\frac{2M}{r}\right)}}-t_{sh}}{\Delta{t_{sh}}} =\underline{ \underline{\frac{1}{\sqrt{\left(1-\frac{2M}{r}\right)}}-1 }}\tag{8}\)
We made it! We found the expression for wavelength received by far-away observer.
Are we finished? Nope :)
Us jellyfishes are curious creatures.
You better watch out Curious George, we might take your spot.
We are interested in what happens when \(r \gg 2M\). When the radius from central mass is much greater than event horizon 2M.
We do this by using Taylor expansions on what we found in equation (8).
\(f(x) = \frac{1}{\sqrt{1-x}} - 1, x = \frac{2M}{r}\)
We do the Taylor expansion of f in point a = 0 of second degree
\(f_2(x; a = 0) = f(0) + f'(0)\cdot(x- 0)\)
\(f_2(x; a = 0) = 0 + \frac{1}{2\sqrt{1-0}^3}x\)
\(f_2(x; a = 0) = \frac{x}{2} =\frac{2M}{2r} = \frac{M}{r}\)
Aha, so for \(r \gg 2M\) we have \(\frac{\Delta {\lambda}}{\lambda_{shell}} = \frac{M}{r}\).
So, if the far-away observer is VERRYYYYY FARRRR away from the black hole. Will he always observe a wavelength that is somewhat always (approximated) M/r? I think that is what it means.
Weird thing worth to mention:
Did you notice the units on \(\frac{M}{r}\) is \(\frac{[kg]}{[m]}\)? How do you divide mass on distance?
You do something very crazy... MEASURE MASS IN METER!
We achieve this by using a natural conversion factor \(\frac{G}{c^2}\). I'll show you how it works.
\(M^{m} = \frac{G}{c^2}M^{kg}\)
Shown in units
\([m] =\left(\frac{ \frac{[kg][m]}{[s^2]}\frac{[m^2]}{[kg^2]}}{\frac{[m^2]}{[s^2]}} \right)\cdot [kg]\)
My mass is 4.827004174927133*10-26 m 😎
(if I calculated that correctly)
Sources:
[1] Lecture notes 2c, section 1