Oppgave 1 - Shannon-Fano-koding og Huffman-koding
a)
Shannon-Fano-oppdelingene blir for denne modellen entydige for en gitt sortering av symbolene (for sortering av symbolene kan vi velge om "b" eller "c" skal plasseres som nest hyppigst). Dersom vi bruker den sorteringen av symbolene som er angitt i modellen og følger forslaget om å etter hver oppdeling tilordne 0 til venstre gruppe og 1 til høyre gruppe, får vi følgende tre:
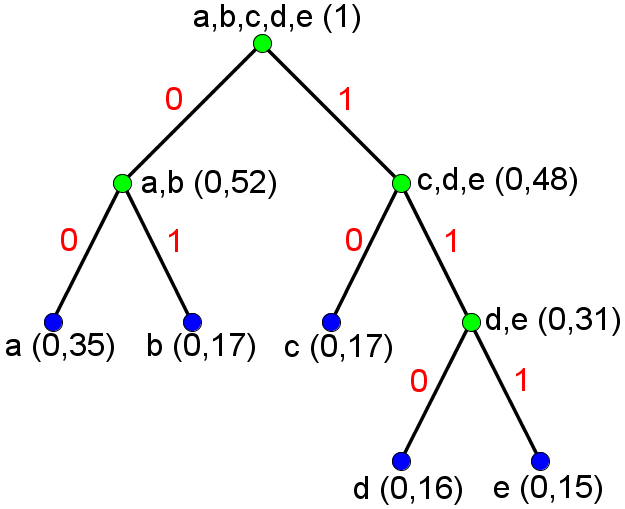
Dette gir følgende kodebok:
| Symbol | a | b | c | d | e |
|---|---|---|---|---|---|
| Shannon-Fano-kodeord | 00 | 01 | 10 | 110 | 111 |
Gjennomsnittlig antall biter per symbol etter Shannon-Fano-koding (når vi koder en melding som har identisk normalisert histogram som den angitte modellen) er gitt som summen av punktproduktet av sannsynlighetene og lengden av Shannon-Fano-kodeordene, som blir 2,31.
b)
Huffman-sammenslåingene blir for denne modellen entydige. Hvis vi følger forslaget på om å etter hver sammenslåing tilordne 0 til den mest sannsynlige gruppen og 1 til den minst sannsynlige gruppen, og definerer at "b" skal bli tilordnet 0 når den slås sammen med "c", får vi følgende tre:
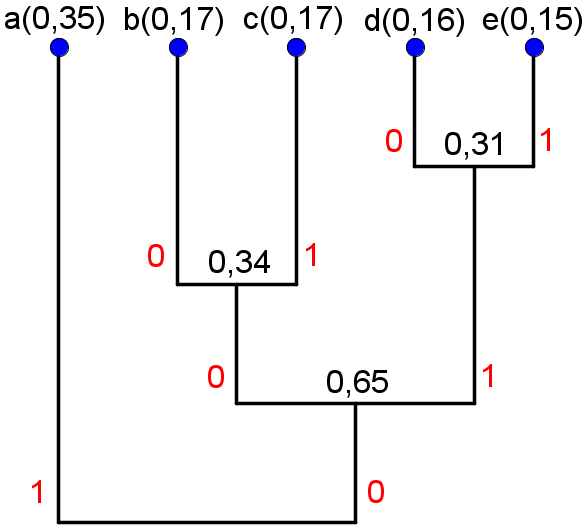
Dette gir følgende kodebok:
| Symbol | a | b | c | d | e |
|---|---|---|---|---|---|
| Huffman-kodeord | 1 | 000 | 001 | 010 | 011 |
Gjennomsnittlig antall biter per symbol etter Huffman-koding (når vi koder en melding som har identisk normalisert histogram som den angitte modellen) er gitt som summen av punktproduktet av sannsynlighetene og lengden av Huffman-kodeordene, som blir 2,3.
c)
d)
Forslag til sannsynlighetsmodell:
| Symbol | a | b | c | d | e |
|---|---|---|---|---|---|
| Sannsynlighet | 0,42 | 0,15 | 0,15 | 0,14 | 0,14 |
Ingen av algoritmene vil oppføre seg annerledes når de anvendes på denne modellen (forutsatt at vi bruker den angitte sorteringen av symbolene), noe som gjør at begge kodebøkene er fortsatt gyldige. Det gjennomsnittlig antall biter per symbol etter Shannon-Fano-koding (når vi koder en melding som har identisk normalisert histogram som den angitte modellen) blir nå 2,28, mens tilsvarende gjennomsnitt etter Huffman-koding blir 2,16.
Bemerkning: Det kan virke som både Shannon-Fano-algoritmen og Huffman-algoritmen "takler" denne modellen bedre ettersom begge gjennomsnittene blir mindre for denne modellen enn den opprinnelige. "Takler" en modell er selvsagt et upresist begrep, men når man studerer kodingsalgoritmer som koder enkeltsymboler er det naturlig å vurdere hvor god en algoritme er ut fra hvor mye kodingsredundans den gjenlater etter koding, altså hvor stor differansen er mellom det gjennomsnittlige bitsforbruket per symbol etter koding og entropien. For den første modellen er entropien omtrent 2,23, og for den andre modellen er entropien omtrent 2,14. Dette vil si at kodingsredundansen øker for Shannon-Fano-algoritmen fra første modell til andre modell, mens reduseres for Huffman-algoritmen. Det virker derfor naturlig å si at Huffman-algoritmen takler den nye modellen bedre, mens Shannon-Fano-algoritmen takler denne nye modellen dårligere, og at grunnen for at begge gjennomsnittene blir mindre for den nye modellen er at denne modellene har mindre entropi og kan derfor (iallfall teoretisk sett) komprimeres kraftigere med kodingsalgoritmer som koder enkeltsymboler.
Oppgave 2 - Huffman-dekoding
Følg hintet og du skal ende opp med meldingen "Digital bildebehandling".
Oppgave 3 - Huffman-koding uten kodingsredundans
En Huffman-kode av meldingen "DIGITAL OVERALT!" er:
| Symbol | ^ | ! | A | D | E | G | I | L | O | R | T | V |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Huffman-kodeord | 1000 | 1101 | 000 | 1010 | 1111 | 1011 | 010 | 001 | 1001 | 1100 | 011 | 1110 |
| Antall forekomster | 1 | 1 | 2 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | 2 | 1 |
der "^" markerer mellomrom.
Vi har i alt 16 symboler, men bare 12 forskjellige, og antall forekomster er enten 2 ("A", "I", "L", "T") eller 1 ("^", "!", "D", "E", "G", "O", "R", "V"). Det betyr at alle de N=12 sannsynlighetene kan skrives som brøker der telleren er 1 og nevneren er en toerpotens (8 eller 16). Altså kan alle symbolsannsynlighetene uttrykkes som 1/2k for forskjellige heltallige verdier av k. I dette tilfellet vet vi Huffman-koding vil gi ingen kodingsredundans, som betyr at entropien er lik det gjennomsnittlige antall biter per symbol etter Huffman-koding. Vi kan derfor finne entropien av denne meldingen ved å beregne gjennomsnittlig antall biter per symbol etter Huffman-koding, noe som ikke innebærer noen logaritme-beregninger.
Når man utfører beregningene finner man at både entropien og det gjennomsnittlige antall biter per symbol etter Huffman-koding er 3,5:
R = (8*3 + 8*4) / 16 = 56 / 16 = 3,5
H = -4*(1/8)*log2(1/8) - 8*(1/16)*log2(1/16) = log2(23)/2 + log2(24)/2 = 3/2 + 4/2 = 3,5
Oppgave 4 - Huffman koding
Se implementasjonsforslag her.
Oppgave 5 - Aritmetisk koding, Huffman-koding og entropi
a)
Symbolene "a", "b", "c" og "d" har forekomster på henholdsvis 2, 1, 2 og 5. Én gyldig fremgangsmåte for Huffman-algoritmen er derfor: I den resulterende Huffman-kodeboken vil lengdene av Huffman-kodeordene bli 3, 3, 2 og 1 for henholdsvis symbol "a", "b", "c" og "d", noe som gjør at gjennomsnittlige antall biter per piksel etter Huffman-koding er 1,8.
- Slå sammen gruppen som består av "a" og gruppen som består av "b", som gir en ny gruppe med total forekomst på 3,
- Slå sammen gruppen som består av "a" og "b" og gruppen som består av "c", som gir en ny gruppe med total forekomst på 5,
- Slå sammen gruppen som består av "a", "b" og "c" og "d" og gruppen som består av "d"
b)
Begynn med [0,1) som "current interval" og beregn nytt "current interval" for hvert symbol (bruk f.eks. formlene på s. 43 i forelesningsnotatet). Det siste "current interval" som du beregner, som vil være det intervallet du velger for EOD-symbolet, skal være omtrent [0,11483761, 0,11483778).
c)
For å finne korteste mulige binære representasjon av et tall i det siste "current interval" så finner vi flere og flere sifre i binærrepresentasjonen av nedre og øvre grense inntil sifferet for nedre og øvre grense er forskjellig. For våre grenser får vi de binære sekvensene 000111010110010... og 000111010110011... for henholdsvis nedre og øvre grense. (Siden begge "..."-delene er ikke-0 vil både 0,0001110101100102 < 0,1148376110 og 0,0001110101100112 < 0,11483778310 - altså er bare det generelle tilfellet i tips 3 i oppgave 6 relevant.) Den korteste mulige binære representasjonen av et tall i intervallet vårt er altså 0,0001110101100112, så den aritmetiske koden for hele meldingen er 000111010110011. (Ved å regne ut den veiede summen av de negative toerpotensene, får vi at 0,0001110101100112 ≈ 0,1148376510.)
d)
Siden det er 15 biter i den aritmetiske koden og 10 symboler i meldingen, vil vi i gjennomsnitt bruke 1,5 biter per symbol etter den aritmetiske kodingen.
e)
Ettersom aritmetisk koding koder flere symboler som ett flyttall, vil dens bitforbruk ikke være begrenset av entropien, ettersom sistnevnte kun er en nedre grense for gjennomsnittlig bitforbruk per symbol når vi koder symbol for symbol.
f)
For enkelte meldinger kan det gjennomsnittlige bitforbruket per symbol etter aritmetisk koding "ved en tilfeldighet"* være mindre enn entropien, men i gjennomsnitt (for uendelig mange og uendelig lange meldinger) så vil det gjennomsnittlige bitforbruket etter aritmetisk koding ikke kunne være mindre enn entropien (dersom de forskjellige posisjonene i meldingen ikke er avhengig av hverandre). Dette er det vi mener med at aritmetisk koding er i gjennomsnitt begrenset av entropien.
Med basis i dette er det naturlig å forvente at kodingsredundansen etter aritmetisk koding av tilfeldige permuteringer av den opprinnelige meldingen vil i gjennomsnitt være positiv. Strengt tatt er mengden av alle disse permuteringene bare en delmengde av alle mulige meldinger, så vi kan derfor ikke direkte bruke sammenhengen beskrevet i forrige avsnitt, men siden den sammenhengen forteller oss at kodingsredundansen generelt vil være ikke-negativ i gjennomsnitt og vi vet fra den nevne simuleringen at aritmetisk koding i gjennomsnitt resulterer i større kodingsredundans desto kortere meldingen er, så er det svært rimelig å tro at kodingsredundansen etter aritmetisk koding av disse permuterte meldingene i gjennomsnitt vil være (endel) større enn entropien.
I en testkjøring der kodingsredundansen etter aritmetisk koding ble beregnet for 1000 tilfeldige permuteringer av den opprinnelige meldingen så ble gjennomsnittlig kodingsredundans omtrent 0,39 (varierte fra -0,26 til 0,54).
* Vi sier at aritmetisk koding bare "ved en tilfeldighet" kan resultere i et bitforbruk under entropien fordi den aritmetiske kodingen baserer seg på en sannsynlighetsmodell som kun angir sannsynligheten for hvert enkeltsymbol, ikke for noen symboltupler (f.eks. symbolpar, symboltripler osv.). Vi kan derfor ikke påstå at aritmetisk koding bevist prøver å utnytte noen form for sammenheng mellom symboler (slik sammenheng kaller vi intersampel redundans). (Det kan faktisk finnes noen svært spesielle scenarioer der samtlige av de genererte meldingene har en intersampel redundans som er slik at aritmetisk koding konsekvent resulterer i et bitforbruk under entropien, noe som vil si at kodingsredundansen i gjennomsnitt er negativ for det (svært spesifikke) scenarioet, men at aritmetisk koding fungerer bra i et slikt scenario bør tilregnes det svært spesielle scenarioet og ikke at det er tilsiktet at aritmetisk koding skal fungere ekstra bra for den aktuelle intersampel redundansen.) (Reduksjon av intersampel redundans er derimot hovedgrunnen til å benytte en høyereordens modell eller en adaptiv modell, og for slike aritmetiske kodinger vil vi naturligvis potensielt kunne oppnå langt større kompresjonsrater.)
Oppgave 6 - Aritmetisk koding
Se implementasjonsforslag her