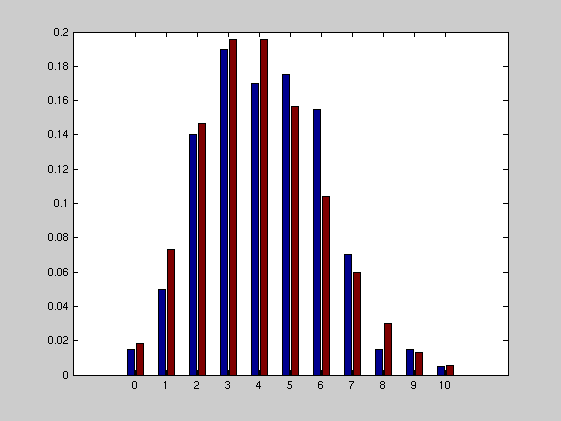
%DATO: 03.03.06 %NAVN: INGUNN FRIDE TVETE %STK1100 %MATLABOPPGAVE 4 %Vi tar her utgangspunkt i uniformt fordelte observasjoner, % og vil med disse generere eksponentielt fordelte observasjoner, % og genererer vidre fra disse en Poisson-prosess. %a) Trekker 1000 observasjoner fra uniform fordeling paa intervallet [0,1]: U=unifrnd(0,1,[1 1000]); hist(U) figure %Kommentar: %soyylene paa mitt histogram ble noksaa like (hoye). %b) Vi vet fra laereboka at hvis U er uniformt fordelt paa intervallet [0,1] %saa vil X=-log(1-U)/lambda vaere eksponentialfordelt med parameter lambda. %Med lambda=1: X=-log(1-U); hist(X) figure %Kommentar: %vi ser at dette histogrammet har fasong som en eksponentialfordeling. %c) Vi genererer en Poisson-prosess fra eksponentialfordelte observasjoner %ved aa la de eksponentialfordelte observasjonene vaere ventetider mellom %begivenheter i Poisson-prosessen. %Poisson-prosess med lambda=1: T=cumsum(X); %d) Hvor mange begivenheter i Poisson-prosessen ovenfor faller i gitte %intervaller: %Deler opp tiden: t=0:4:800; %Teller opp antall begivenheter: N=histc(T,t); %e) Teller opp hvor mange intervaller som har 0,1, ..., 10 begivenheter: x=0:10; y=histc(N,x); bar(x,y); figure %f) Vi sammenligner de relative frekvensene for den simulerte prosessen med %punktsannsynlighetene i en Poisson-fordeling med parameter lik 4. relfr=y/200; punktsanns=poisspdf(x,4); %Vi sammenlinger, %enten skriv: relfr=relfr(:); punktsanns=punktsanns(:); sanns=[relfr punktsanns] %Vi ser at kolonnene i sanns matrisen samsvarer rimelig godt. %Vi plotter: %enten skriv: bar(x',sanns)
sanns =
0.0150 0.0183
0.0500 0.0733
0.1400 0.1465
0.1900 0.1954
0.1700 0.1954
0.1750 0.1563
0.1550 0.1042
0.0700 0.0595
0.0150 0.0298
0.0150 0.0132
0.0050 0.0053