Askeladden rotet rundt i den store eksen sin med det rare i. Han finner fram teleskopet sitt, setter det opp på høyre siden av båten og drar fram den gode gamle datamaskinen laget av tre. Han ville gjerne se om han kunne finne noen stjerner med planeter rundt og om stjernene beveger seg bort fra ham.
Han setter teleskopet sitt til å se på hastigheten til en stjerne langt, langt unna. Det teleskopet gir er en kurve som oscillerer. «Merkelig, den skulle jo vært rett.» grubler Askeladden. Han tenker på hva en oscillerende hastighetskurve betyr og kommer på at det betyr at stjernen beveger seg i ring. Man kan se at lyset som kommer fra stjernen endrer seg på lysspekteret fra rødforskyvet til blåforskyvet. Hvorfor bruker ikke han bare vinkelen som utbreder seg mellom stjernen og planeten? spørr du. Jo, den er så utrolig liten at vi klarer ikke å separere stjerne og planet på slike enorme avstander!
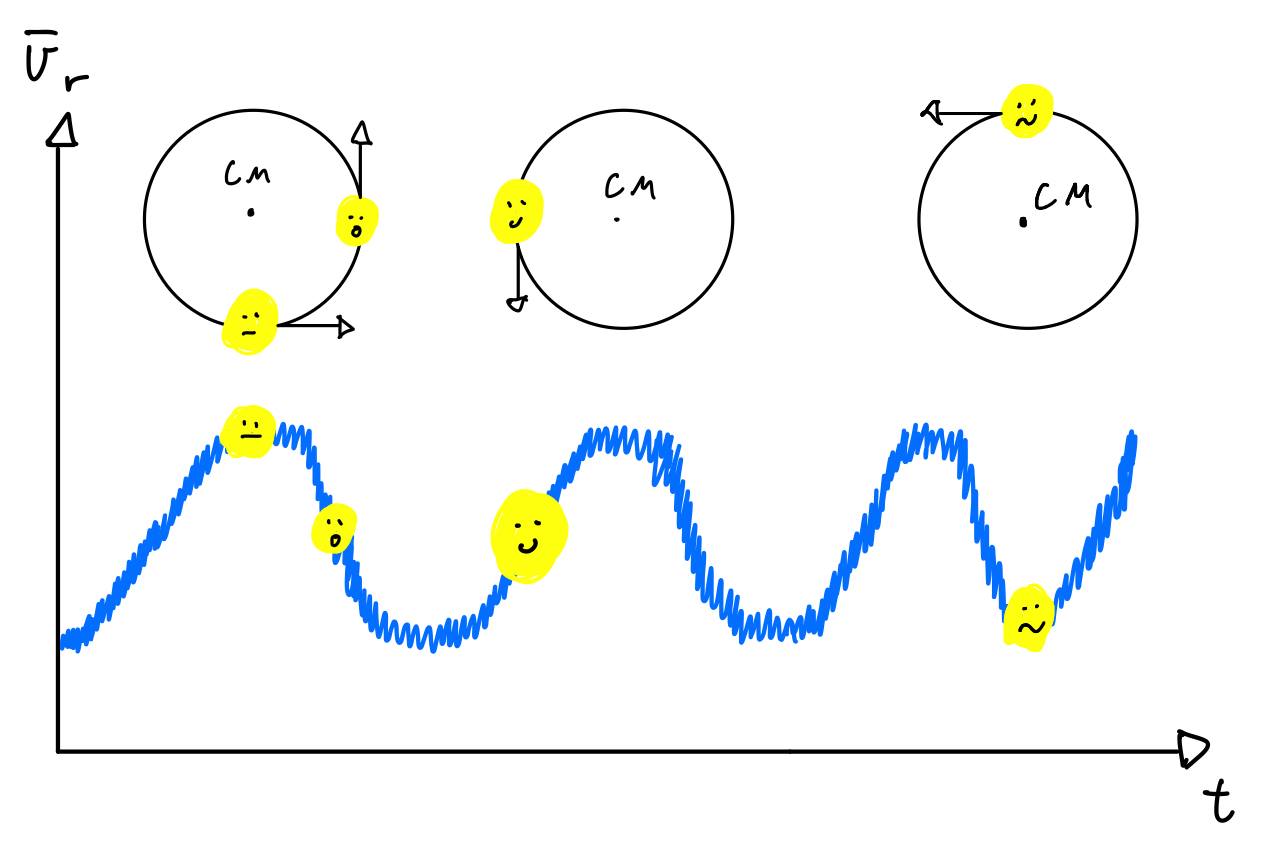
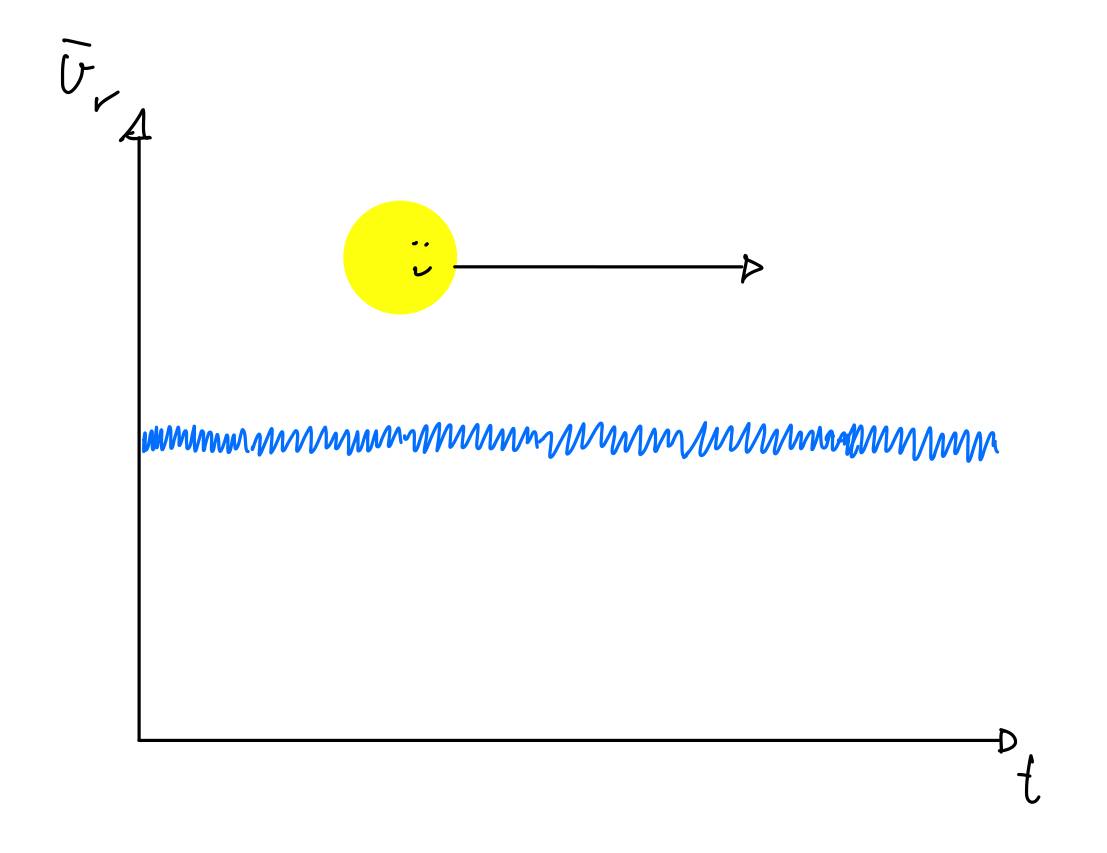
Askeladden har jo drømt om dette som heter massesenter. Det at stjerna beveger seg i ring betyr at det er en planet rundt stjerna, fordi planeten drar på stjerna like mye som stjerna drar på planeten. Dette kan vi se i figur 1. Hadde stjernen ikke hatt en planet hadde denne radielle hastighetskurven vært konstant ved en hastighet, som man kan se i figur 2.
Når han observerer lyset fra andre stjerner legger Askeladden merke til at dataene han får er litt tykke. Ved nærmere inspeksjon så ser han at det er sammensatt av mange små "opp-" og "nedturer" langs observasjonsspekteret. Han roter fram bråkknuseren som han har liggende i båten. Denne knuser grafen ved å se på dataene som fører til det minste avviket mellom det Askeladden ser og den estimerte kurven som passer best til dataene.
Nå som Askeladden skjønte at det er en planet rundt stjerna han ser på. Vil han gjerne finne ut hvor stor denne kan være, både masse og radius. En ting som Askeladden finner ut når han tegner teleskopet som peker på stjerna er at hvis normalen til systemet er 90 grader på synslinjen hans, så kan han se at lyset til stjerna dupper av. "Hva kan nå dette bety?" tenker Askeladden med blyanten mellom ørene. "Det må jo være fordi noe blokker for stjerna!" roper Askeladden ekstatisk. Han skriver og tegner febrilsk en sketsj av hvordan det kan se ut i figur 3.
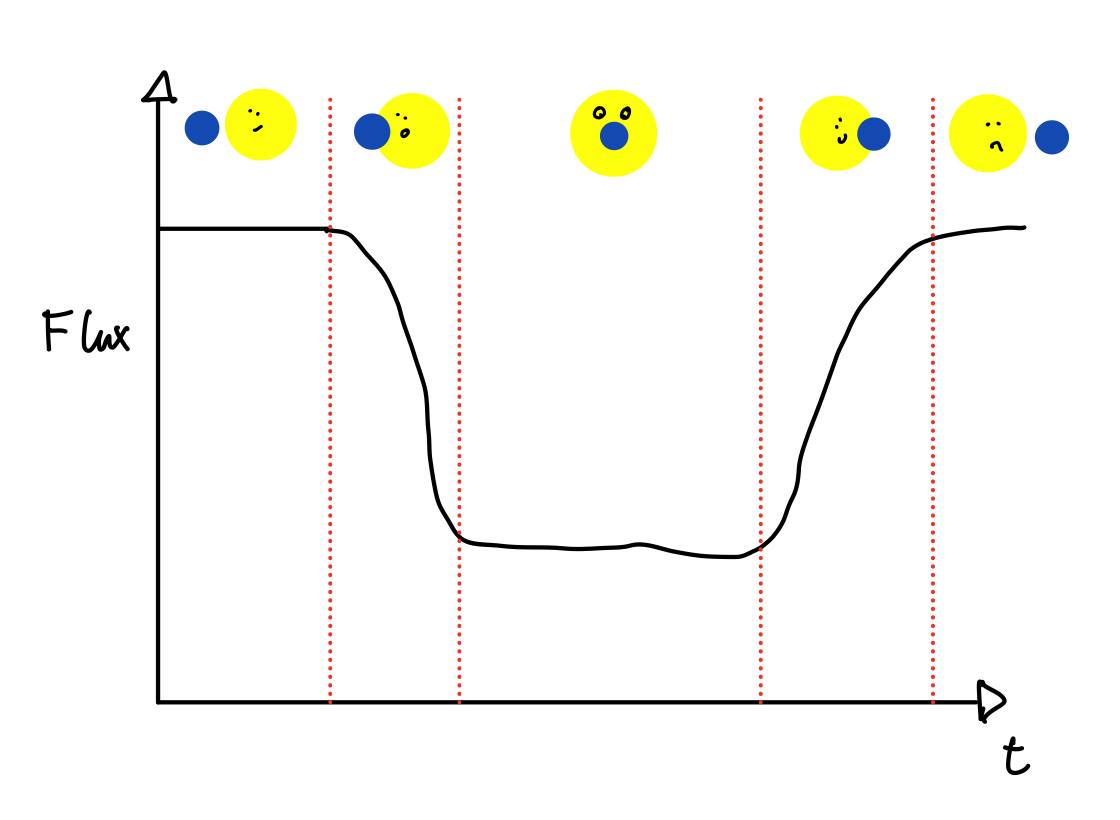
Han ser at i det planeten begynner å dekke stjerna så går lys styrken lineært nedover til den stopper. "Det må da vel bety at diameteren til stjerna kan finnes ved å se på tiden den bruker å dekke stjerna og hastigheten den har." uttrykke Askeladden. Han uttrykket det i en formel som vist under:
\(D = 2R_p = \vec{v}_p \cdot (t_1 - t_0)\), her er \(\vec{v}_p\) hastigheten til planeten, \(R_p\) er radiusen til planeten, \(t_1\) er tiden da hele planeten skygger for sola og \(t_0\) er tiden før den begynner å skygge for stjernen.
Men hvordan i all verden finner man hastigheten til planeten? Vi vet jo hastigheten til stjernen ved å se på endringen i bølgelengden fra dopplereffekten av lyset som kommer til teleskopet, grunnet bevegelsen til stjernen rundt massesenteret. Vel, vi deriverte jo vektorene som peker på legemene fra massesenter systemet som \(\vec{r}_{1, CM}, \vec{r}_{2, CM}\). Tar vi forholdet mellom disse to vektorene og litt angulær hastighets ekstravagansa får vi uttrykket under:
\(\frac{|\vec{r}_{2, CM}|}{|\vec{r}_{1, CM}|} = \frac{\frac{\mu}{m_2}\vec{r}}{\frac{\mu}{m_1}\vec{r}} = \frac{m_1}{m_2} = \frac{v_1}{v_2}\), hvor \(m_1\), \(v_1\) er massen og hastigheten til planeten og \(m_2\), \(v_2\) er massen og hastigheten til stjernen sett fra massesenteret.
Vi kan fra denne finne hastigheten til planeten gitt ut ifra begge massene til legemene og den radielle hastigheten til stjerna. Men vi har jo ikke massen til planeten, så har vi kommet noe lengre egentlig? Askeladden klør seg i hodet og tenker på hvilke sammenhenger man har til massen til planeten ut i fra det han vet.
Askeladden husker det han lærte fra vandreren Newton om omløpsperioden til legemet rundt stjernen og at store halvakse i massesentersystemet kan skrives som \(a = a_{\odot} + a_p\). Dette er summen av store halvakse til stjerna (\(a_{\odot}\)) og store halvakse til planeten (\(a_p\)). Det kan da vises at massen til planeten (\(m_1\)) ved en inklinasjonsvinkel på \(i \approx 90^\circ\) ender opp som:
\(m_1 = \frac{m_2^{2/3} v_{2, r} P^{1/3}}{(2\pi G)^{1/3}}\), massen til planeten er dermed avhengig av den radielle hastigheten til stjernen og perioden til planeten om massesenteret.
I den fine formelen over er den minste massen til planeten gitt som \(m_1\). Minste massen? spørr du. Ja, sier eg. Vi ser på tilfelle hvor solsystemet står normalt på synsretningen vår, altså at inklinasjonsvinkelen er \(i = 90^\circ\). Dermed får vi at den minste mulige massen er \(m_{1}sin(i) = m_{1, min}\). Den radielle hastigheten til stjerna rundt massesenteret er gitt som \(v_{2, r}\). G er den universale gravitasjonskonstanten gitt som \(G = 6.67\cdot 10^{-11}\) [\(m^3 kg^{-1}s^{-2}\)] og P er perioden til stjerna gitt i gitt i sekunder.
Hva skal nå Askeladden gjøre med all denne informasjonen? Jo, han skal gjøre litt ap på Tuslingen!
Kilder
- Forelesningsnotater Part 1B og Part 1C av Frode Hansen, https://www.uio.no/studier/emner/matnat/astro/AST2000/h21/undervisningsmateriell/lecture_notes/
