Kva gjer Askeladden i verdsrommet dersom han ikkje kan sjå rundt seg og finne ut kvar han befinn seg? Det kan ikkje vere enkelt å navigere seg fram utan å sjå noko. Men kva er det som kan hjelpe Askeladden med å navigere? Heldigvis var det mor hans som hadde pakka sekken. Askeladden var stor gut og pissa sjølv, men det å pakke eigen sekk kunne han vente nokre år til med. Mor til Askeladden hadde nemleg pakka med eit toppmoderne kamera! Med dette kameraet montert på ei roterande skive på toppen av masta, kunne han ta bilete rundt seg og endeleg finne ut kvar han var.
Men hadde mor hans tenkt såpass langt som å lage programvare til dette kolossale kameraet? Neida! Her måtte Askeladden trå til sjølv!
Merk: Denne bloggposten vert lang, så sløyng frå deg tøflane, len deg godt attende, og la hovudet synke inn i eventyrmodus der alt frå troll og hekser til fysikkens lovar er ekte.
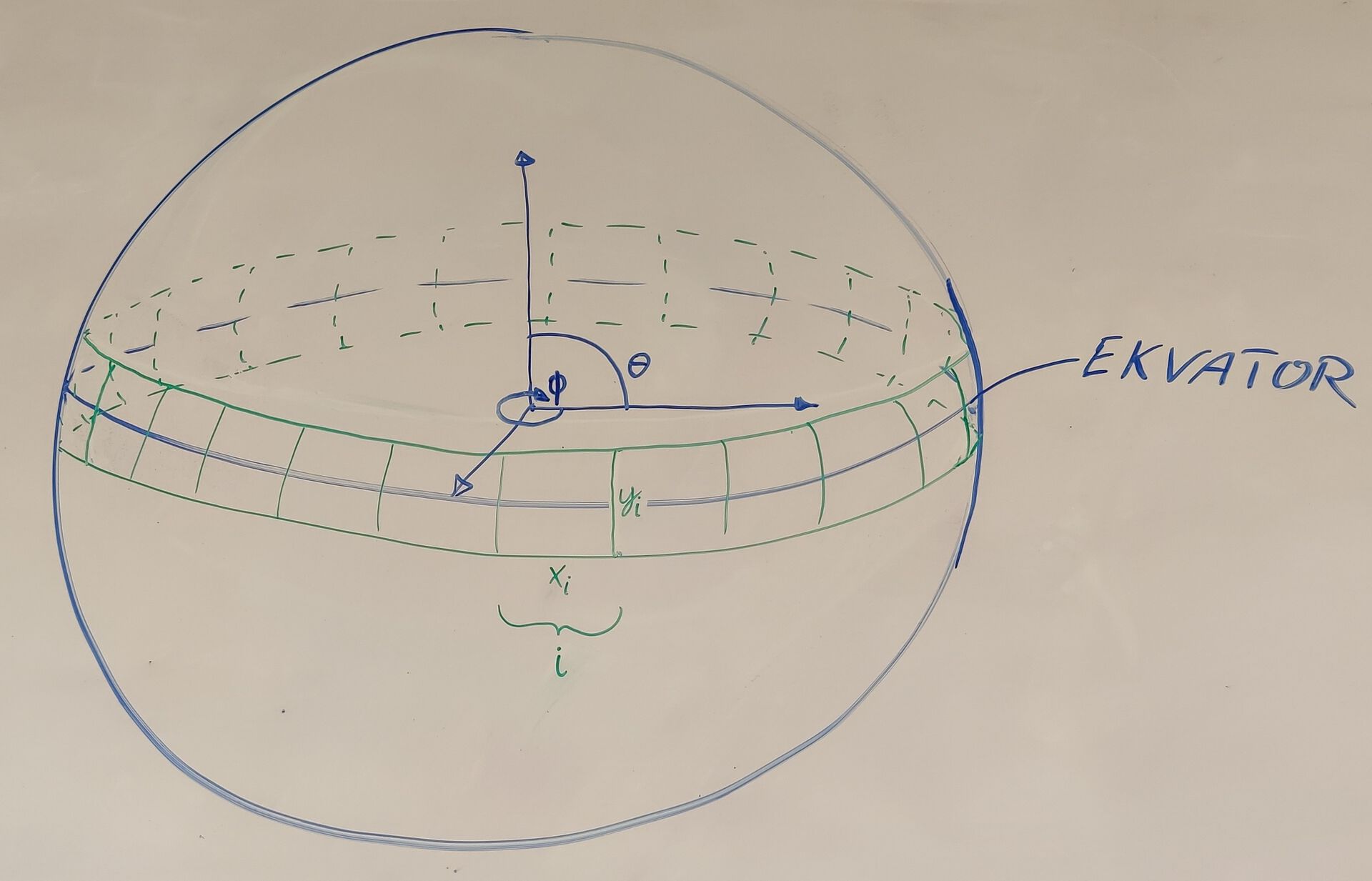
Så kvar skal vår kjære Askeladden byrje? Han har altså ei himmelkule han skal ta bilete av, men korleis ser denne himmelkula ut? Sjå for deg at du svevar åleine i verdsrommet. Kanskje litt einsamt, men la oss anta at det er triveleg. Du er då i sentrum av ei kule, ei sfære om du vil, og alle stjernane, planetane og alt anna av omgjevnadar dekkjer heile innsida av denne kula. På ein måte måla på innsida av kula. Det er dette som er himmelkula, og for å gjera det noko enklare å drive med, vil vi berre bekymre oss for regionen rundt ekvator på denne kula. Sjå Figur 1 nedanfor for ei skisse av himmelkula.
Med andre ord: kameraet er posisjonert i sentrum medan det roterar \(360^\circ\) og tek bilete av ekvatorregion.
"Panoramabilete vil fungere fjell her", tenkte Askeladden.
"Har du sedd på utstyret ditt, gut? Kameraet ditt er da ein Nokia 3310. Dei kjem ikkje med panoramafunksjon", svarte Tuslingen som plutseleg kom på at han kunne lese tankar.
Kva med å dele opp ekvator i 360 delar? Ikkje dumt! Då kan vi byrja på \(\phi_0 = 0^\circ\), ta eit bilete, flytte oss til \(\phi_0 = 1^\circ\) og ta eit bilete, osv. Sjå figuren nedanfor.
Men så må vi òg vite kor stort dette bilete skal vere. Heldigvis hadde Askeladden fått med seg eit dømebilete av Reodor som han kan bruke som mal. Så her er det berre å hive seg igang!
Som sagt så må vi fyrst vite kor stort dette dømebiletet er. Det kan gjerast ved å opne biletet i koda og så lage ein array av sjølve biletet. Då står vi med ei matrise som inneheld alle pikslane i biletet. Med ein funksjon som heiter Numpy.shape() kan vi finne storleiken av biletet i x- og y-retning, som viser seg å vere høvesvis 640 og 480 pikslar. Det er mange pikslar å gå gjennom! Kvar og ein av desse pikslane skal vi nemleg bruke til å finne RGB-verdiane til biletet vi skal ta, men det kjem vi tilbake til seinare. For dei som lurar står RGB for Red, Green, Blue, som er primærfargane.
Men før det må vi rekne ut minimums- og maksimumsverdiane av x og y. Vi kjem ikkje langt med berre storleiken. Likninga for \(x_{max/min}\) og \(y_{max/min}\) hadde Askeladden kome fram til på førehand i ein draum han hadde. Den ivrige matematikaren kan finne ei særs rask utleiing her.
\(x_{max/min} = \pm \frac{2 \sin(\alpha_{\phi}/2)}{1 + \cos(\alpha_{\phi}/2)} \\ y_{max/min} = \pm \frac{2 \sin(\alpha_{\theta}/2)}{1 + \cos(\alpha_{\theta}/2)}\)
I bruksanvisninga på Nokia'n står det at \(\alpha_{\theta}=\alpha_{\phi}=70^\circ\) som er synsfeltet (field of view) til kameraet. Det er dette som er grensa til kvart enkelt bilete. Nokia'n er ikkje så god at han kan ta eitt bilete av alt skjønar du.

"Men akk og ve!", stønna Tuslingen. "Dette gjev oss da eit vanleg flatt bilete. Korleis i reine skafte verd skal vi bruke dette til å få fram bilete av noko sfærisk? Himmelkula er sfærisk, Askeladden!"
Men så positiv og roleg som Askeladden er så var det enkelt å ignorere bekymringane til Tuslingen. Askeladden hadde nemleg lært litt om stereografisk projeksjon like før dei la ned skulen i bygda. Denne teknologien vil føre til at mannskapet ombord veit i hvilken retning skipet peker i. Fra den informasjonen kan man få full kontroll over både hastighetsvektor og sikt for å komme seg fram i det tre-dimensjonale rommet.
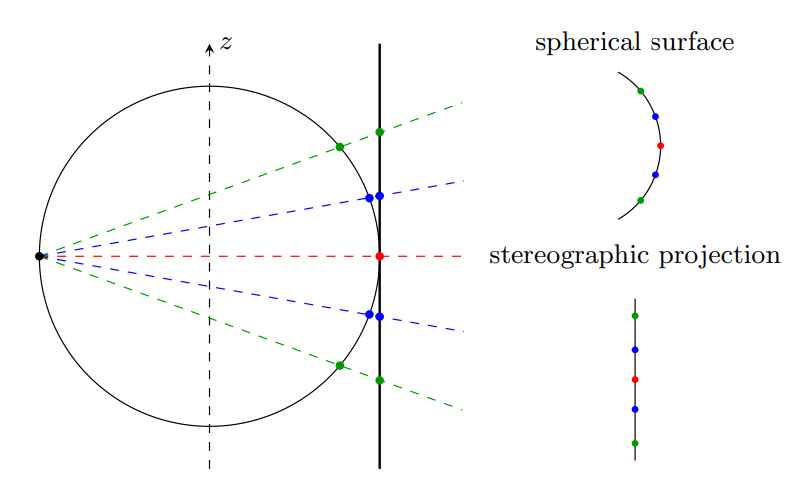
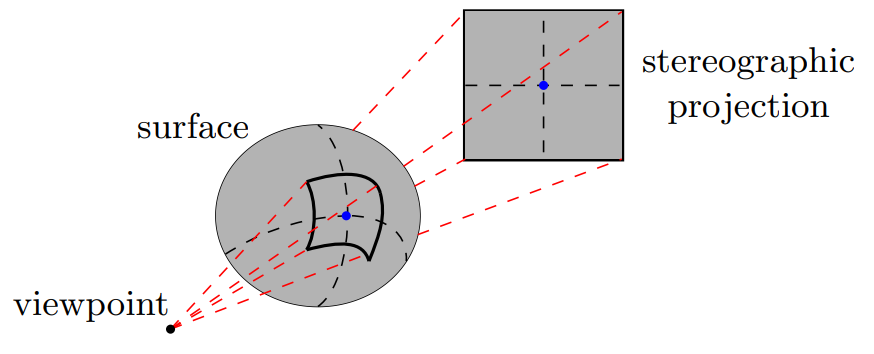
Når Askeladden no tek eit bilete, vil det bilete han får vere flatt. Heng med så langt? Flott! Dette flate biletet er ein såkalla stereografisk projeksjon av himmelkula han tek bilete av, sjå figurane over. Men korleis veit kameraet kva for fargar som er i kvar piksel på biletet? Det er det vi må rekne ut! Vi må omgjere kvar kartesiske koordinat \((x, y)\), altså kvar piksel, i denne stereografiske projeksjonen til sfæriske koordinatar \((\theta, \phi)\), for så å hente ut RGB-verdiane for alle pikslane. Desse RGB-verdiane vil vi då bruke for å sette saman biletet. Merk at vi her driv i eit todimensjonalt system. Vi let sentrum av bilete vere i \(x = y = 0\). Koordinattransformasjonen frå \((x, y)\) til \((\theta, \phi)\) blir då
\(\theta = \theta_0 - \arcsin \left[\cos\beta \cos\theta_0 + \frac{y}{\rho} \sin\beta \sin\theta_0 \right] \\ \phi = \phi_0 + \arctan \left[\frac{x \sin\beta}{\rho \sin\theta_0 \cos\beta - y \cos\theta_0 \sin\beta} \right]\) ,der \(\rho = \sqrt{x^2 + y^2} \\ \beta = 2 \arctan \left(\frac{\rho}{2} \right)\).
Korleis kom Askeladden fram til denne, lurar du sikkert på no. Dette var noko av det nyttige Tuslingen kom med ein sjeldan gong, så dette må Askeladden berre godta.
Dersom Askeladden lagar seg eit grid, eller nett som vi seier på godt norsk, kan han no ved hjelp av koordinattransformasjonane gjere dette nettet om til eit sfærisk nett, hente ut RGB-verdiane i alle rutanen (pikslane) i dette nettet, for så å leggje dei til i biletet sitt.
Då er det berre for Askeladden å dengje dette inn i furumaskina som han måtte spikke ny Backspace-knapp til førre veke, og ...
... poof!


"Men kva i alle dagar", mumlar Askeladden i det han tek opp referansebiletet frå Reodor og samanliknar det med det han nettopp fekk. "Tusling! Vi har eit problem!"
Biletet er feil veg! Kva skal Askeladden gjere no?
"Neimen, sjå dær. Nå pratar vi!", seier han plutseleg.
Tuslingen ser bort på Askeladden som sit der med datamaskina opp og ned i fanget sitt.
"No veit eg det!", utbryt Askeladden. Modulen han brukar for å produsere desse bileta er kalla PIL, ein slags modul spesifikt for bilete i Python. Kanskje inneheld den noko som kan snu bilete for han? Det gjer det! Ein funksjon kalla ImageOps som han kan importere har noko som heiter ImageOps.flip(). Her er det berre å leggje til biletet og ... voila!

"Eg må innrømme at eg er særs kreativ til tider", seier Askeladden, tydeleg stolt over sin eiga innsats. "Det var ein enkel måte å ordne problemet på. Nesten for enkelt. Eg har på følinga at dette sikkert kjem til å kome attende som nok eit problem for meg seinare, men det er eit problem for framtidige meg. No er det kaffepause!"
Denne bloggposten tek til å bli særs lang, så da kan det kanskje vere lurt å ta seg ei lita pause med noko godt i koppen.

Etter ei alt for lang kaffepause, ein liten blund og nokre lefserullar med spekeskinke teken frå stabburet heime på garden, hiv Askeladden seg inn i det vidare arbeidet med ny giv.
Han går nå eit steg vidare og set kameraet til å ta bilete for alle \(\phi \in [0^\circ , 360^\circ]\). Det var jo det som var den originale tanken. Resultatet ser du i den nydelege videoen under, der du kan skimte 360 forskjellige bilete satt saman til ein liten video:

"Då var me endeleg ferdige med det", sa Askeladden og ga seg sjølv ein klapp på skuldra.
"Ferdig?", spurte Tuslingen forundra. "Kva meiner du med ferdig? Vi veit da ikkje kva for ei retning vi ser i på bileta"
"Sjølvsagt veit vi det!", svara Askeladden medan han tok opp eit av bileta. "Vi ser den vegen".
"Og kva for ein veg er det?"
"Den vegen"
"Kvar?"
"Dit"
Det er berrsynt at det er noko som manglar her. Det er berre Askeladden som ikkje vil innrømme det, lat som han er.
Askeladden sat seg ned og følte seg tufsete og dom, men så høyrte han eit sus som over furukrona kom.
"Eg ga deg fleire referansebilete", sa suset med noko som likna veldig på stemma til Reodor.
Tuslingen såg seg fortusta rundt om på skipet før han fekk auge på datamaskina til Askeladden. Den hadde byrja å vekse på seg ei ny krone på toppen av skjærmen.
Med fleire referansebilete å ta utgangspunkt i, kan vi ved hjelp av minste kvadraters metode gå over alle bileta og samanlikne dei med kvart enkelt referansebilete. Når programmet finn ein match, eller fyrstikk som vi seier på norsk, kan vi få det til å printe ut verdien til \(\phi\) som bileta matcha på. La oss halde oss til ordet match, fyrstikk høyrer ikkje heilt rett ut. Ved minste kvadraters metode tek vi å minimaliserar skilnaden mellom ein modell vi har og dataa vi får. For å finne den minste skilnaden tek vi dataa minus modellen og opphøgjer denne skilnaden i andre potens, derav namnet "minste kvadrat". Vi kvadrerar for å få absoluttverdien. Vi er ikkje interessert i forteiknet til skilnaden.
Og då kjem det store spørgesmålet. KVA skal vi samalikne? Kva er det vi skal finne skilnaden mellom på desse bileta? Kan du gjette deg fram til det? Du kan det nok. Njaaa, nærmar deg nå. Nesten..... Yes! RGB-verdiane! Her er referansebileta modellen vår, dei bileta vi tek med kameraet er dataa vi samlar inn, og RGB-verdiane er dei vi skal samanlikne.
Er ikkje det ein enkel sak? Jauda, men ikkje gløym at vi må gå gjennom RGB-verdiane i kvar piksel... i kvart einaste bilete! Dette gjer vi ved å få programmet til å ta utgangspunkt i det fyrste referansebiletet, lèt det gå over bileta vi tek og samanliknar. Og når det finn eit som har ein skilnad lik null i RGB-verdiane får vi programmet til å spytte ut \(\phi\)-verdien, for så å ta neste referansebilete og byrje på nytt.
Dette kjem nok til å ta ei stund.
Men no støytar vi på eit problem. Hugsar du ImageOps.flip()? Vi brukte det til å koste problemet om at bilete vi fekk var opp og ned under teppet, men no har teppet plutseleg drege opp skjørtet og gått sin veg. Og problemet ligg der nå og blottar seg på skipsgolvet for alle å sjå!
ImageOps.flip() viser seg å fungere berre på det ferdige produktet, altså på det ferdige biletet vi har laga. Og nå skal vi ikkje bruke biletet, men det det er bygd opp av, nemleg matrisa med alle RGB-verdiane, eller nettet med alle pikslane som inneheld alle RGB-verdiane er vel kanskje meir rett å seie. Dette nettet blir ikkje snudd av flip'en vår. Vi må tenkje nytt.
Transponering av matriser! Det er noko dykk ikkje vil lære før dykk er på det store universitetet, men kort og godt handlar det om å "snu" på ei matrise. Nå er det ikkje slik at vi snur matrisa opp og ned, men vi snur slik at vi får eit rett nett av pikslar til biletet. Slik kan Askeladden endeleg få orden på problemet sitt. Askeladden gjer så dette, og endeleg er alt slik det skal vere. Eller er det? Time vil shjåvv.
Programmet køyrer, Nokia'n dirrar som ein gammal Saab som har stått brisen i to timar, og ut blir det printa ein \(\phi\)-verdi som skal samsvare med det fyrste referansebiletet, \(\phi = 0\). No er det berre å vente på det neste, som tek ei god stund. Neste verdi blir utprinta! \(\phi = 20\), som skal samsvare med det andre referansebiletet. Då er det berre å vente på neste!
...
Men så går det ei stund.
...
Så går det nok ei stund.
Plutseleg kjem det endå ei stund å går forbi.
Etter at den fjerde stunda kjem tuslande forbi kahyttglaset, tenkjer Askeladden som så at her må det vere noko gale. Programmet køyrer og køyrer, men inga ny \(\phi\) dukkar opp. Askeladden kjem til bilete 240 før han gjev opp. Programmet klarer altså å matche dei to fyrste referansebileta, men ikkje det neste. Kva kan vere feil her tru? Askeladden prøvar seg fram med å hoppe over referansebilete nummer tre og pluggar nummer fire direkte inn i programmet.
Og tida går...
... det tek si tid dette programmet her. Det er noko vi kan ta til etterretning. Programmet kan nok mest sannsynleg effektiviserast ein del, men det er det inga tid til akkurat no. Det ser heller ikkje ut til at det er noko bilete som vil matche med det fjerde referansebilete.
Askeladden gjev opp etter å ha sedd gjennom nesten 300 av dei 360 bileta sine. "Dette er håplaust", seier han, "men vi har da to \(\phi\)-verdiar! Det er meir enn nok synes eg!"
"Nja", svarar Tuslingen skeptisk, "men alle gode ting er tre".
"Her er litt tre", seier Askeladden medan han sagar av den nyvokste krona på datamaskina og kastar den bort til Tuslingen.
Det er berrsynt at det er noko som ikkje stemmer i programmet. Etter at Tuslingen fekk overtala Askeladden til å sjå over kodinga si ein gong til, som var ein særs tidkrevjande prosess som inneheldt både blod, svette og tårer vel å merke, fann Askeladden til slutt ut at noko måtte vere gale med måten han samanliknar RGB-verdiane.
Måten vi eigentleg tenkte å samanlikne desse på var å plukke ut kvar enkelt av dei tre grunnfargane, og sjå om skilnaden til kvar enkelt var lik null. Det kan hende at det kanskje er eit for trangt nålauge å tre noko gjennom. Kanskje skilnaden i RGB-verdiane ikkje treng å vere lik null, men berre vere særs liten for at bileta skal matche. Men om dei da ikkje er lik null, er bileta dei same?
Dette er spørsmål stakkars Askeladden ikkje har tid eller hjernekapasitet til å tenkje over no. Han og Tuslingen må nemleg kome seg vidare før problema hopar seg opp. Det er ikkje berre kvar og kva dei ser dei må finne ut, men òg kva for ein hastigheit dei har!
Kjelder:
[1] https://www.uio.no/studier/emner/matnat/astro/AST2000/h21/undervisningsmateriell/prosjektlop/prosjektdeler/part4.pdf
