Askeladden trenger også et system for å finne hastigheten til båten når den drifter gjennom solsystemet. Han kan bruke det han vet om analyse av stjernene til å finne hastigheten til romskipet ved å finne hva den radielle hastigheten til de er. Vi analyserer spektrallinjen til hydrogen-alpha for å finne hastigheten til to stjerner. Hydrogen-alpha spektrallinjen oppstår når ionisert hydrogen gir fra seg energi som et foton. Siden stjerner for det meste brenner hydrogen ved overflaten, er denne den sterkeste linjen som vi kan se. Bølgelengden til H-alpha (\(H_\alpha\)) i laboratoriet er 656.3 [nm]. Med laboratoriet mener vi at energien blir sluppet fra et ionisert hydrogen som er i "ro". Askeladden har tegnet hvordan han fant bølgelengden i figur 1.
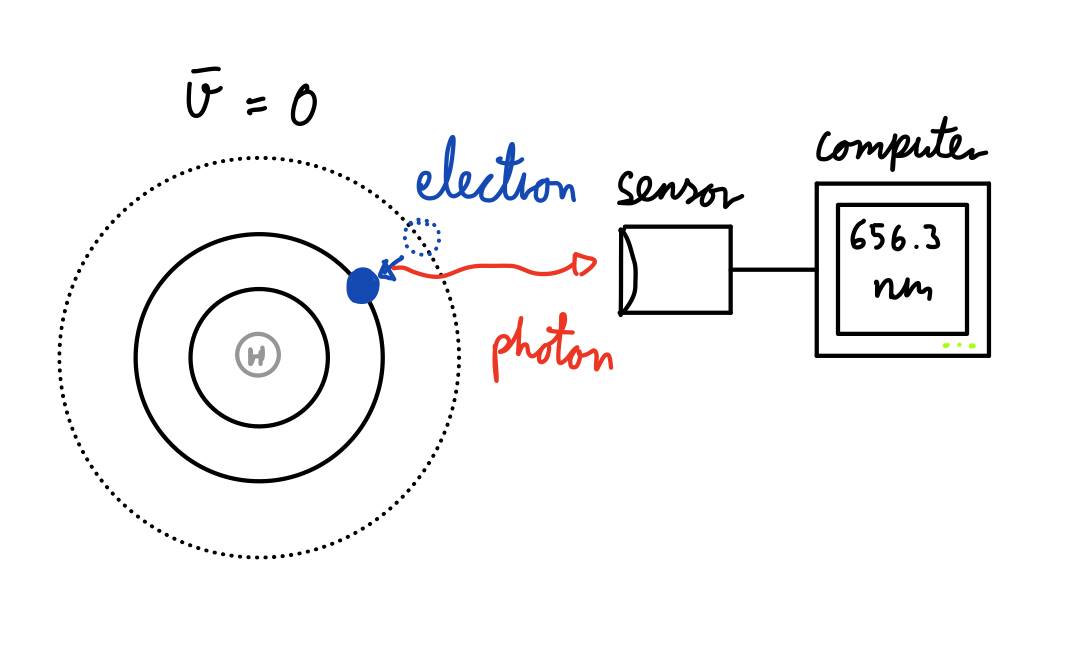
Denne bølgelengden vil være vår referanse bølgelengde \(\lambda_0\) [nm]. Grunnen til at Askeladden trenger en referanse bølgelengde er på grunn av doppler effekten som vi lærte om i et tidligere innlegg. Den forteller oss at endringen i bølgelengde relaterer direkte til den radielle hastigheten til stjernen om massesenteret sitt! Formelen som vi beskriver er
\(\frac{\lambda - \lambda_0}{\lambda_0} = \frac{\Delta\lambda}{\lambda_0} = \frac{v_r}{c}\), hvor \(v_r\) er den radielle hastigheten om massesenteret, \(c\) er lyshastigheten og \(\lambda\) er den målte bølgelengden til stjernen Askeladden ser på.
Vi kommer til å trenge hva den radielle hastigheten til stjernen \(v_r\) er, så Askeladden skriver om formelen over til
\(v_r = \frac{\Delta\lambda}{\lambda_0}c\), her er det kun brukt brøkregler.
Askeladden og Tuslingens team, med Reodor Felgen i front, nede på Tvønnoing har funnet posisjonsvinkelen til to stjerner som Askeladden kan bruke og sender det med post opp til båten. Disse to vinklene er med respekt til x-aksen og gitt i grader. Vinklene er som følger \(\phi_1 \approx 154.4^\circ \approx 2.695\) [rad] og \(\phi_2 \approx 78.7^\circ \approx 1.372\) [rad]. Tilsvarende bølgelengdeforskjeller var også vedlagt med postfuglen Solan, gitt som \(\Delta\lambda_{\phi_1} \approx -0.00347\) og \(\Delta\lambda_{\phi_2} \approx 0.0119\). Den ene forskjellen er negativ, mens den andre forskjellen er positiv. Vi husker at om forskjellen er negativ er spekteret blåforskyvet og objektet beveger seg mot oss, positiv forskjell betyr rødforskyvet og objektet beveger seg dermed bort fra oss. Vi kan se at forholdene mellom vinklene er vist godt i figur 2 og forteller oss hvordan disse stjernene er plassert ut i fra båtens posisjon.
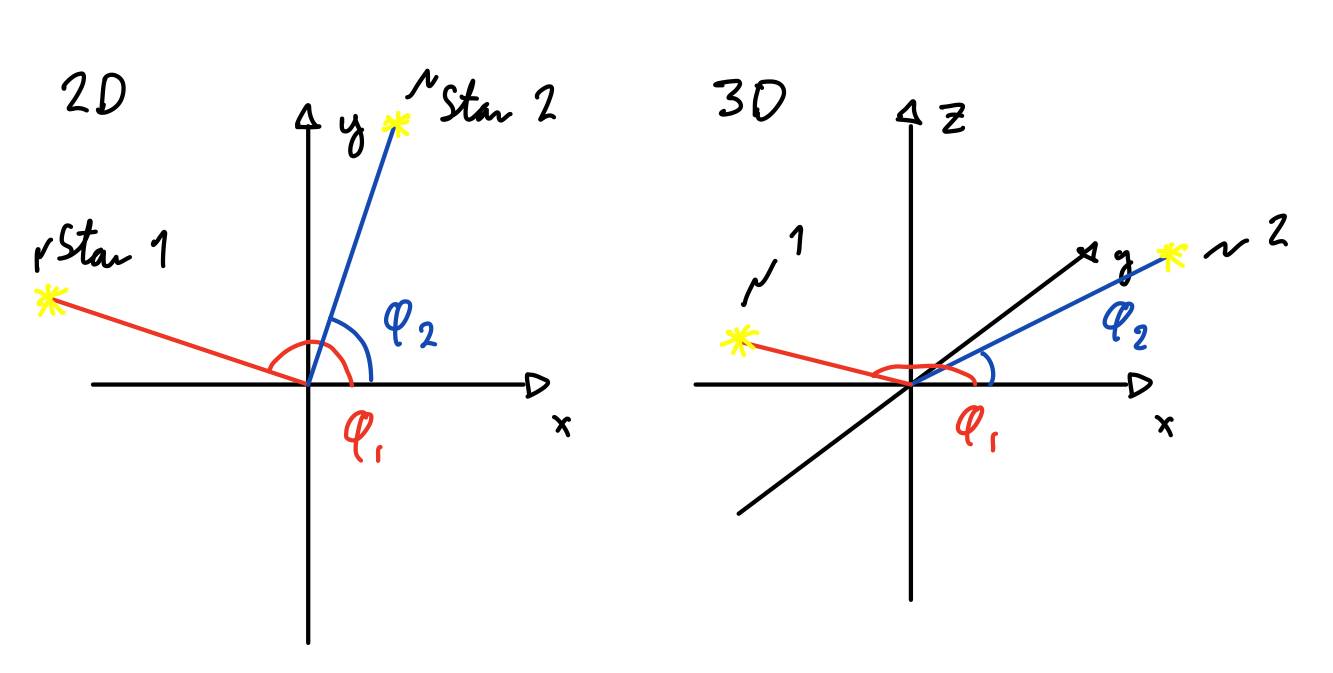
Askeladden tar verdiene og spikker de inn i formelen. Han antar at de stjernene vi ser på er så langt borte at de står stille. Da finner vi at den radielle hastigheten til første stjerne er \(v_{r, \phi_1} = -0.33\) [AU/år] og andre stjerne er \(v_{r, \phi_2} = 1.145\) [AU/år]. Vi frisker opp minne litt og gjenforteller at [AU/år] er hastighetsmål som forteller hvor stor del av avstanden mellom jorda og sola man dekker på et år. Når Askeladden sjekker spektrografen på båten, ser han at den viser at bølgelengdeforskjellene til de to stjernene er \(\Delta \lambda_{\phi_1} = \Delta \lambda_{\phi_2} = 0\)! Hva betyr nå det? Askeladden tenkte og tenkte... "Da må jo jeg sitte i bilen!" ropte han ut! Han hadde nemlig tenkt at hvis man står å ser på en bil som kjører forbi, vil man kunne måle hastigheten til den bilen. MEN, om man sitter inne i den samme bilen og prøver å måle hastigheten så vil måleren vise 0! Båten har dermed samme hastighet som stjernen i forhold til referanse stjernene! Disse hastighetene er dessverre ikke gitt i xy-planet som vi jobber i. Dermed må vi konvertere de ved hjelp av en transformasjon som ser slik ut:
\((d_x, d_y) = \frac{1}{\sin(\phi_2 - \phi_1)}\begin{pmatrix}\sin\phi_2 & -\sin\phi_1 \\ -\cos\phi_2 & \cos\phi_1\end{pmatrix}(d_1, d_2)\), dette ser ut som tung matte, men det er ikke så veldig vanskelig. Den transformerer sfæriske koordinater (\(\theta, \phi\)) om til kartesiske som vi er vant til (x, y). Om du er interessert kan du finne utledning og forklaring i kildene til Askeladden.
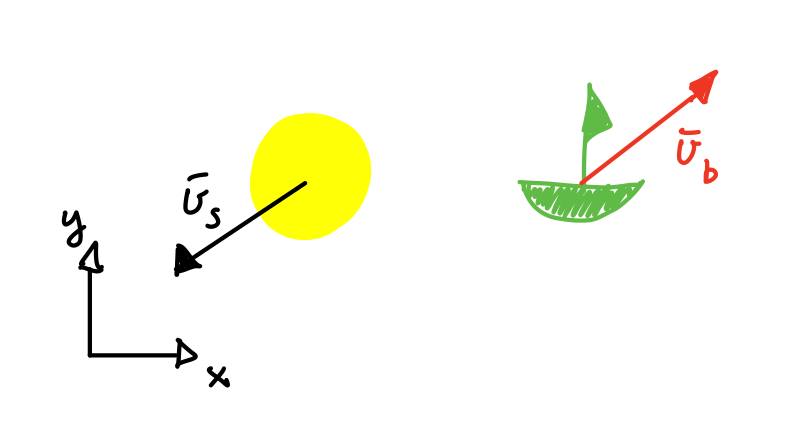
Hastigheten i xy-planet kan dermed finnes ved å multiplisere verdiene for hastighetene i sfæriske koordinater \((v_{r, \phi_1}, v_{r, \phi_2})\) med matrisen i formelen over, som vi kaller \(u\). Askeladden finner da at båten sin hastighet er gitt som \((v_x, v_y) = (v_{r, \phi_1}, v_{r, \phi_2}) \cdot \hat{u} = (-0.84, -0.99)\) [AU/år]. Men, stemmer nå egentlig dette? Om hastighetene i forhold til stjernen er gitt i en bestemt retning og romskipet måler ingen doppler forskjell, må jo hastigheten til båten være motsatt av doppler effekten. Hastigheten til båten kompenserer for doppler effekten og må dermed ha en hastighet som er motsatt av den som blir målt fra stjernen. Den endelige farten til båten er dermed \((v_x, v_y) = (0.84, 0.99)\) [AU/år] i dette tenkte tilfelle. Hastighetsvektoren i forhold til xy-planet er vist i figur 3.
Den første delen av denne figur 3 viser hastighetsvektoren til solen i forhold til båten i xy-planet. Hastighetsvektoren til båten bør dermed være det motsatte av det Askeladden ser fra båten og hastighetsvektoren er dermed tegnet inn i figur 3 i motsatt retning.
Vi er helt enige med deg, AU/år forteller oss egentlig ingen verdens ting. Askeladden gjorde derfor vektoren om til noen enheter vi kjenner, nemlig [km/t]. Nysgjerrig på hvordan han gjorde konverteringen? Sjekk journalen hans. Han endte dermed med \((v_x, v_y) = (14486, 17038)\) [km/t]! På en motorvei hadde denne hastigheten skaffet deg en heftig bot, men hastigheten for å opprettholde en geosentrisk bane rundt jorda (som betyr at man beveger seg med rotasjonen) må hastigheten til satelitter ligger rundt \(11000\) [km/t]. Båten sin hastighet er dermed ikke fysisk usannsynlig i dette eksempelet.
Et annet potensielt problem i våre antagelser er hvordan vi har definert det geometriske rommet. Askeladden og Tuslingen har diskutert mye mellom seg hvordan vinklene i forhold til x-planet skal tolkes. Det er fullt mulig at vinklene er definert feil ut i fra det referansesystemet de har fulgt. Grunnen til at vi lurer på dette er at sjekken som Reodor Felgen har sendt oss, sier at hastighetene er feil. Dette kan også bety at magnituden til hastighetene er feil, men siden vi allerede har argumentert for at de ikke er det så har vi antatt at de er korrekte. En annen potensiell feil er at omgjøringen fra sfærisk til kartesisk i simuleringen er implementert feil. Askeladden brukte vektorkalkulus for å skjøte transformasjonen sammen i simuleringen, men han la merke til at hastighetene endret seg da han endret på måten dette ble lagt inn i simuleringen. Størrelsene endret seg altså ved å endre på transformasjonen.
Tiltross for at denne metoden har mulige feil, så laster Askeladden simuleringen opp i båten for senere estimering av hastigheten. Så, hva er nå posisjonen til båten i solsystemet?
Kilder
[1] AST2000 - Part 4, https://www.uio.no/studier/emner/matnat/astro/AST2000/h21/undervisningsmateriell/prosjektlop/prosjektdeler/part4.pdf
