En viktig ting å alltid vite er hvor man er! I tilfelle mor ringer eller du skal møte noen. Askeladden er nødt til å vite til enhver tid hvor båten hans befinner seg i solsystemet. Han har med en radar som vet nøyaktig hvor langt det er til alle planetene fra der han er og til stjernen. Han vet også hvilken posisjon hver planet har til stjernen, til enhver tid! Med dette kan han finne posisjonen til båten. Du kan se for deg at du står på en ganske tom parkeringsplass med tre biler, en rød, en blå og en lilla. Hvilken av parkeringsplassene står du på? Ekkoloddet du alltid går med i lomma forteller deg at du står 4 plasser unna den blå bilen, 3 plasser unna den rød og 2 plasser unna den lilla bilen. Askeladden har tegnet scenarioet i figur 1. Setter man et punkt for alle mulige parkeringsplassene du står på, basert på parkeringsplasser mellom deg og bilene får man mange punkter på plassen. Men, om du studerer tegningen til Askeladden er det kun en parkeringsplass som stemmer med alle avstandene. Du befinner deg på parkeringsplassen i øverste rad nr. 7 fra venstre.
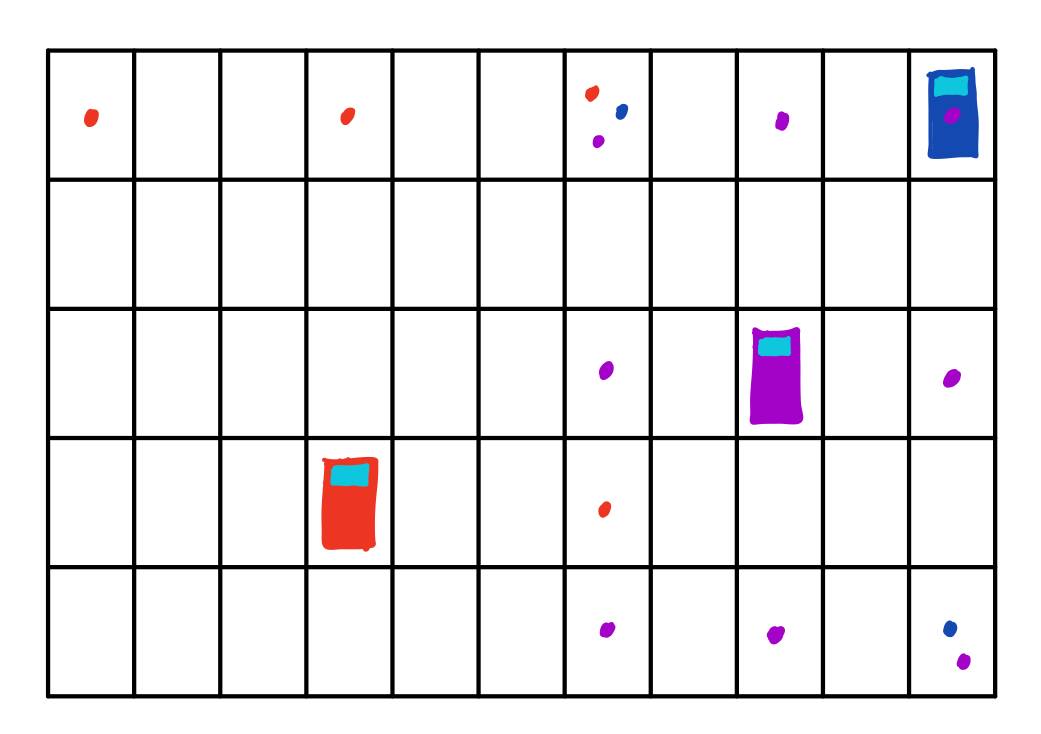
Denne metoden kalles multilaterasjon og er en måte å finne posisjon på ved å måle avstander til kjente objekter. Askeladden brukte nettopp dette til å finne posisjonen til båten sin. La oss se på hans tegning av båten og avstandene til både stjernen og planetene. Denne tegningen ser du i figur 2.
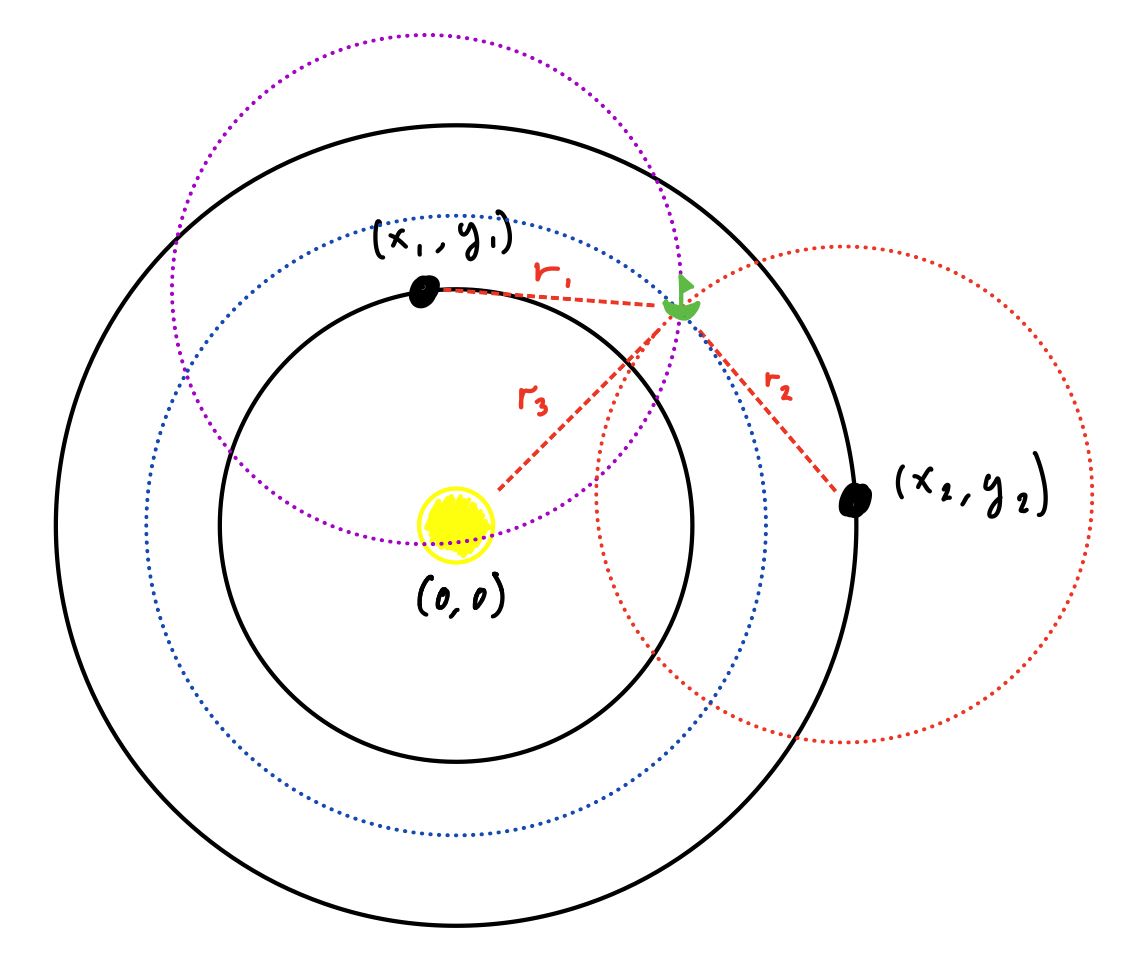
Det er ikke særlig stor forskjell fra figur 1 og figur 2 i det heletatt, kan du se det? I figur 2 kan du se stjernen i midten med to planeter i bane rundt den. Vi har tegnet båten i grønt for å skille fra de andre fargene. Båten vet nøyaktig avstand fra stjernen og det Askeladden gjør, er å tegne en sirkel rundt stjernen med blått som har radiusen til den målte avstanden. Akkurat slik vi gjorde med parkeringsplassen. Dette gjør han med planet 1 og planet 2 også, og bruker fargene rød og lilla som på parkeringsplassen. Ser du at alle de tegnede sirklene kun krysser på et punkt? Dette er posisjonen til båten i nøyaktig dette tidspunktet. Husk at planetene beveger seg over tid, så om vi lar tiden gå må vi konstant måle avstanden til planetene for å holde posisjonen vår.
Da Askeladden skulle simulere sirklene brukte han den generelle formelen for en sirkel gitt som \((x - x_0)^2 - (y - y_0)^2 = r^2\), hvor \((x_0, y_0)\) er posisjonen til sentrumet av sirkelen og \(r\) er radiusen. Han skriver en formel uttrykt for stjernen og båten og en for for hver av planetene under:
\(\begin{align}(x - x_0)^2 - (y - y_0)^2 &= r_0^2 \\ (x - x_1)^2 - (y - y_1)^2 &= r_1^2 \\ (x - x_2)^2 - (y - y_2)^2 &= r_2^2\end{align}\), disse trekker vi fra hverandre og får to uttrykk som tilsvarer x og y posisjonen til båten!
Interessert i hva Askeladden gjorde? Da kan du lese i journalen hans! Han kom fram til at x-posisjonen og y-posisjonen til båten kunne uttrykkes som to likninger vist under:
\(x = \frac{FB - EC}{BD - AE},\quad y = \frac{FA - DC}{AE - BD}\), her er ABCDEF konstanter som du kan finne i journalen om du er nysgjerrig.
Båten er som nevnt utstyrt med radar som kan definere avstandene fra båten til alle legemene i Pjokknes. Den har også simuleringen til Askeladden, hvor man kan plotte inn dato og klokkeslett å få ut alle planetenes posisjon. Han har dermed alt han trenger for å finne båten. Vi tester ut teorien ved tidspunktet hvor båten er skutt opp og 500 km fra overflaten. Da får Askeladden et plott man kan se i figur 3.
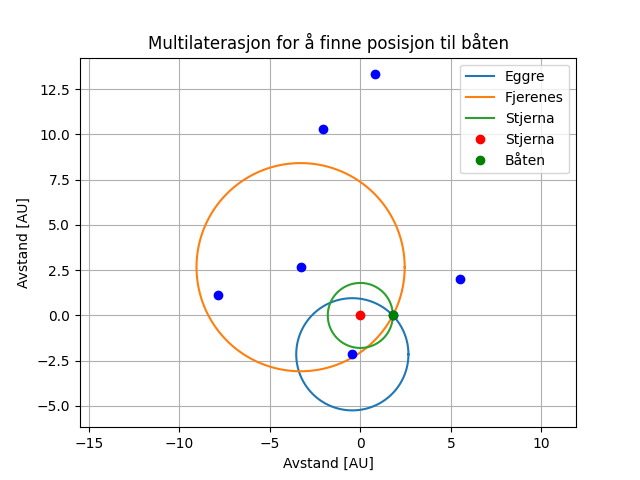
I figur 3 har Askeladden testet metoden for trilaterasjon i tidsrommet hvor båten befinner seg 500 km over hjemplaneten Tvønnoing. Den minste grønne ringen representerer avstanden til stjernen i Pjokknes. Båten kan befinne seg hvor som helst på denne sirkelbanen. Den blå ringen representerer avstanden fra Eggre til båten og den oransje ringen avstanden fra Fjerenes til båten. Vi kan se at om du kombinerer to sirkler så krysser de hverandre på to punkter. Legger vi til en tredje sirkel så krysser disse tre sirklene kun i ett punkt og der ligger båten vår. I figuren kan vi se at båten ligger rett over planeten Tvønnoing. Det er vanskelig å se på grunn av oppløsningen til plottet. Forstørrer vi bildet får vi figur 4.
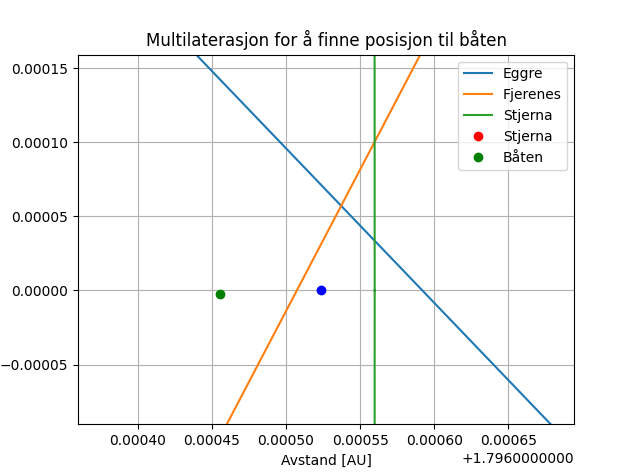
I denne figuren kan vi se at båten befinner seg på samme y-verdi som planeten Tvønnoing. Dette lover bra siden vi skyter den rett opp fra ekvator. En annen ting vi kan se tydelig er at sirklene Askeladden har tegnet er ikke nøyaktige nok til å stemme med beregningen.
Det han kan gjøre for å forberede denne modellen er å bytte mellom planeter etterhvert som de er en viss avstand fra båten. Akkurat i denne simuleringen så har Askeladden bestemt seg for to faste planeter som han bruker iløpet av hele reisen. Hva om simuleringen tok hensyn til en avstandsgrense? Altså om båten hadde vært en viss avstand fra objektet så hadde det objektet blitt neglisjert. Det vi mener er at beregningen blir gjort med de tre nærmeste objektene. Vi hadde da blitt nødt til å modifisere formlene for A, B, C, D, E og F, men det er ikke mye som skal til før denne simuleringen kan bruke dette. Grunnen til at vi vil se på de nærmeste objektene for posisjon er for å jobbe med avstander i samme størrelsesklasse, som igjen hindrer feilkalkulasjon. Hadde man for eksempel brukt avstanden til Giås, Tvønnoing (hjemplanet) og Åtvekdal da båten hadde vært 500 km over Tvønnoing så hadde ikke verdiene like nøyaktige fordi avstanden til Giås er så enormt stor sammenlignet med Tvønnoing.
En god implementering av dette hadde vært å sjekket alle avstandene som blir målt av radaren på båten, funnet de tre minste avstandene og notert hvilke objekter det gjelder for å hente ut posisjonene til de. Desto mindre forskjell det er mellom avstandene, jo mer nøyaktig vil posisjonen til båten være.
