Det var mykje fram og attende, og mykje diskusjon rundt bordet når det kom til utføringa av den planlagte reisa til Askeladden og Tuslingen. Men til slutt kom dei seg endeleg av garde, og alt gjekk som planlagt! Dei to astronautane støyta sjølvsagt på problem undervegs, spesielt når det kom til programvara på skipet. Dei fekk nemleg ikkje skipet til å gå dit dei ville. Men etter ei radiosamtale tilbake til kommandosenteret på Flåklypatoppen, fekk dei tilsendt ei sårt trengjande oppdatering til skipets hovuddatamaskine. Og på eit blunk var dei framme ved Åtvekdal!
Dramatisk musikk medan planeten nærmar seg meir og meir, og auga til Askeladden vert større og større.
Dei er i bane! Men er ho stabil? Korleis ser bana ut? Kva er hastigheita, posisjonen og alt det der til skipet? Dette er verkeleg viktig å finne ut, og det kan vi finne ut på følgjande måte:
No har vi nemleg eit tolekamsystem, slik som i del 2, berre at her er dei to lekamane planeten og skipet.
Avstanden frå skipet til sentrum i planeten \(\vec{r}\), finn vi ved å ta avstanden frå stjerna til planeten \(\vec{r}_{*, p}\), og trekkje frå avstanden frå stjerna til skipet \(\vec{r}_{*, s}\). Det gjev oss \(\vec{r} = \vec{r}_{*, p} - \vec{r}_{*, s}\).
Dette kan vi bruke til å finne den radielle hastigheitskomponenten \(v_r\) til skipet i høve planeten, altså den hastigheitskomponenten som peikar inn mot stjerna. Det gjer vi ved å ta prikkproduktet mellom hastigheitsvektoren \(\vec{v}\) og einingsvektoren \(\hat{r} = \frac{\vec{r}}{|\vec{r}|}\). Dette gjev oss \(v_r = \vec{v} \cdot \frac{\vec{r}}{|\vec{r}|}\).
Då står det berre att å finne den tangentielle hastigheitskomponenten \(v_{\theta}\) til skipet i høve planeten. Her må vi rett og slett måle avstanden vi reiser over eit tidsintervall i bana vår. Men vil ikkje den avstanden vere forma som ei boge? Jau, men no skal dykk høyre her. Det er det som er så fint med å vere fysikar og rakettforskar. Vi kan berre sjå på eit veeeldig lite tidsintervall, og utifrå det seie at avstanden er ei rett linje. Kjekt! No har vi ein trekant vi kan jobbe med. Og kva er det fyrste vi tenkjer på når vi har ein trekant? "Pytagoras!", ropar Askeladden høgt. Her er dei to kjende sidene i trekanten posisjonsvektorane til skipet ved to forskjellige tidspunkt. Dei kan vi bruke til å finne den siste sida i trekanten, \(\Delta s\). Med denne og tidsintervallet \(\Delta t\) finn vi den tangentielle hastigheita: \(v_{\theta} = \frac{\Delta s}{\Delta t}\).
Endeleg kan vi kome oss vidare med å finne litt meir ut om bana vår!
No skal vi rekne ut store halvakse, \(a\), av bana vår, noko som vi lenger ned vil vise kvifor vi treng. Men kva er store halvakse? Det er rett og slett den største avstanden vi kan ha frå sentrum av bana. Kva treng vi til det? Fyrst treng vi apoapsis og periapsis. Apoapsis er avstanden frå det punktet i bana der vi er lengst unna planeten, medan periapsis er avstanden frå det punktet i bana der vi er nærmest planeten. Tek vi summen av desse to og delar på 2, får vi store halvakse: \(a = \frac{apoapsis + periapsis}{2}\).
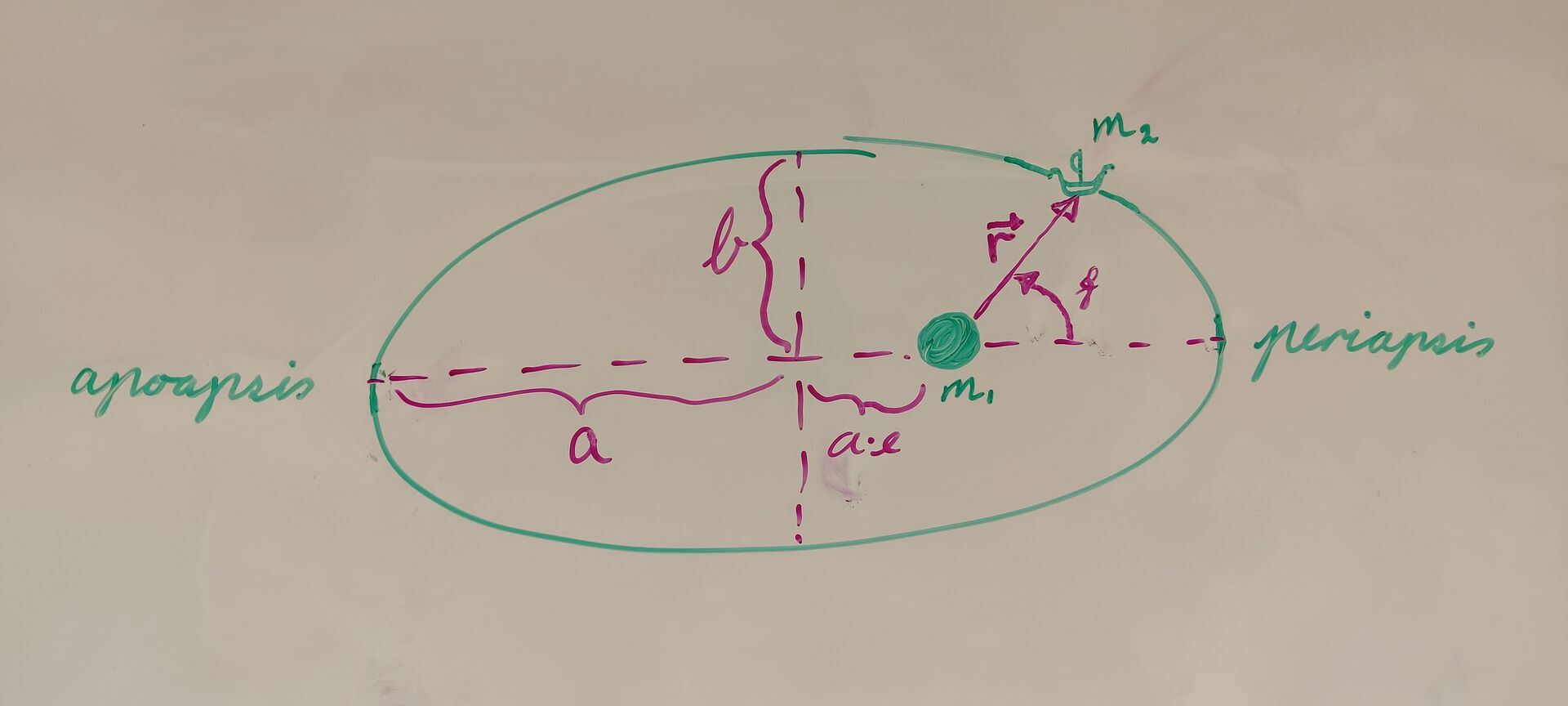
Denne treng vi til å finne vesle halvakse, b. Men før vi går rett til vesle halvakse, må vi innom eksentrisiteten, og før vi går til den må vi innom avstanden mellom sentrum av bana og planeten. Altså der det er merka med \(a \cdot e\) på biletet. La oss kalle denne avstanden \(c\) sidan Askeladden allereie er så godt igang med alfabetet. Grunn til at det står \(a \cdot e\) er rett og slett fordi avstanden \(c\) er produktet av store halvakse og eksentrisiteten. Då kan vi jo finne eksentrisiteten ved å ta differansen av \(c\) og \(a\)! "Genialt!" huar Askeladden. Men korleis finn vi \(c\)? Sjå litt på biletet no. Vi tek berre apoapsis minus store halvakse!
Då har vi \(c\), og når vi har \(c\) har vi eksentrisiteten. Og når vi har eksentisiteten har vi vesle halvakse! Endeleg! No kan vi kome oss vidare og finne omlaupstida \(P\), eller perioda som nokon òg kallar det. Og korleis reknar vi ut den? "Anar ikkje", seier Askeladden som ikkje gadd å tenkje seg om ein gong, lat som han er. Men hadde Askeladden tenkt seg godt om hadde han hugsa på møtet sitt med Kepler og Newton, som vi omtala tidlegare i bloggen. Med den Newtonifiserte versjonen av Keplers tredje lov, finn vi omlaupstida: \(P^2 = \frac{4\pi^2}{G(m_p + m_s)}a^3\), der \(m_p\) er planetmassa og \(m_s\) er massa til skipet. \(G\) er, som alle fysikarar bør vite, gravitasjonskonstanten.
Med alt dette legg vi eit særs godt grunnlag for å stadfeste om vi er i ei stabil bane eller ikkje. Og dersom Askeladden er lur (noko vi berre kan draume om) vil han og Tuslingen gjere fleire omlaup for å VERKELEG stadfeste tala deira, og sjekke kor stabil ei bane dei har. Eksentrisiteten vil her fortelja oss kor ideell og stabil ei bane vi har. Ei sirkelbane viser seg nemleg å vere den mest stabile bana vi kan ha! Des større eksentrisiteten er, des meir ustabil bane har vi.
Dersom eksentrisiteten er null, er bana sirkulær. Dersom ho er mellom null og èin, er bana elliptisk. Dersom eksentrisiteten er èin er bana parabolsk, og dersom eksentrisiteten er over èin, er bana hyperbolsk.
Når alt dette er utrekna og ferdiggjort, kva då med ... å nei! Datamaskina tok fyr!
"Shields up, red alert!"
