Dei modige astronautane våre skal no bevege seg nærare planeten, og med det kan det lønne seg for Askeladden å endre på kva for einingar han bruker i programmet sitt. I staden for å bruke AU i høve til stjerna i systemet skal han no bruke SI-einingar i høve til planetens sentrum. Grunn til dette er at ... vel, har dykk nokon gong høyrt at ISS går i ei bane med ei høgd på \(\approx 2.73 \cdot 10^{-6}\) AU?
Noko som diverre vert utelate i førre bloggomgang var ein video av den stabile bana til S.S. Draumen. Det var grunna omfattande anleggsarbeid som gjekk føre seg mellom Åtvekdal og Tvønnoing, men Askeladden hadde endeleg fått gjennom ei sending til glede for dei som sat heime i stova med auga klistra i fjernsynet.

Astronautane våre skal altså gå ned til ei lågare bane. Men dei kan ikkje gå for lågt, då vil dei nemleg støyte på atmosfæra og alt helvete vil vere laus. Dei må heller ikkje ha for høg eller låg hastigheit. Går hastigheita ut av styring får dei ei meir og meir ustabil bane, noko dei ikkje vil ha. Og blir hastigheita for låg kan det òg hende at dei ikkje vil klare å halde seg oppe og, som nemnd, støyte på atmosfæra. Nei, dei må ha ei stabil hastigheit, \(v_{stabil} = \sqrt{\frac{GM_p}{r}}\) der \(G\) er gravitasjonskonstanten, \(M_p\) er massa til planeten og \(r\) er avstanden frå planetsenteret til skipet. Her er det særs viktig å huske på at vi skal rekne i SI-einingar, og då kan det lønne seg å gonge planetmassa med massa til Sola i ditt system og ikkje massa til stjerna i Pjokknes!
Nett no befinn dei seg i ei bane om lag 4 778 817 m over planetsenteret. Litt obrukeleg tal så la oss trekkje frå planetradien som er \(R \approx 3778817 \) m. Då ligg dei om lag 1 000 000 m over overflata til planeten, eller 1 000 km om du vil. Til samanlikning går den Internasjonale Romstasjonen i ei bane om lag 400 km over jordoverflata. Men kor lågt ned skal Askeladden og Tuslingen gå?
Dette må dei finne ut seinare etter at dei har modellert atmosfæra. Det kan nemleg lønne seg å vite kvar atmosfæra byrjar før dei set i gang ein injeksjonsmanøver.
Ein viktig parameter i dette injeksjonsmanøverprogrammet som Askeladden må skrive er dimed radiusen han vil at dei skal ha til planetens sentrum. Og denne radiusen avheng av atmosfæra. Legg han radiusen inn i formelen for stabil hastigheit får han ut kva for ei hastigheit dei må ha for den ynskte bana.
La oss samanlikne med Jorda. Der definerar man at atmosfæra sluttar og verdsrommet byrjar ved 100km over havet (det er inga brå slutt, men ein jamn overgang), men sjølv ISS som sirkulerar 400km over overflata vert påverka og må rebooste seg opp att nå og da. Satellittar som driv med jordobservasjon ligg på 500-600km for å unngå dette. Kan vi ikkje då bruke det som utgangspunkt?
Finn vi ut kvar atmosfæra vår "sluttar", kan vi ta utgangspunkt i jordobservasjonssatellittar og leggje bana vår 400km over slutten på atmosfæra vår.
Når Askeladden skal kome seg ned til ei lågare bane, er det som vi allereie har nemnt viktig å få ei stabil bane. Dersom bana allereie er ganske stabil vil dette ikkje bli noko særleg problem, men er bana allereie stabil? Som det vert skildra i førre bloggomgang så kan man sjekke om bana er stabil ved å rekne ut eksentrisiteten og sjå kor nærme null den er. Men vi kan òg sjekke avstanden vår frå sentrum av planeten i eit jamnt tidsintervall.
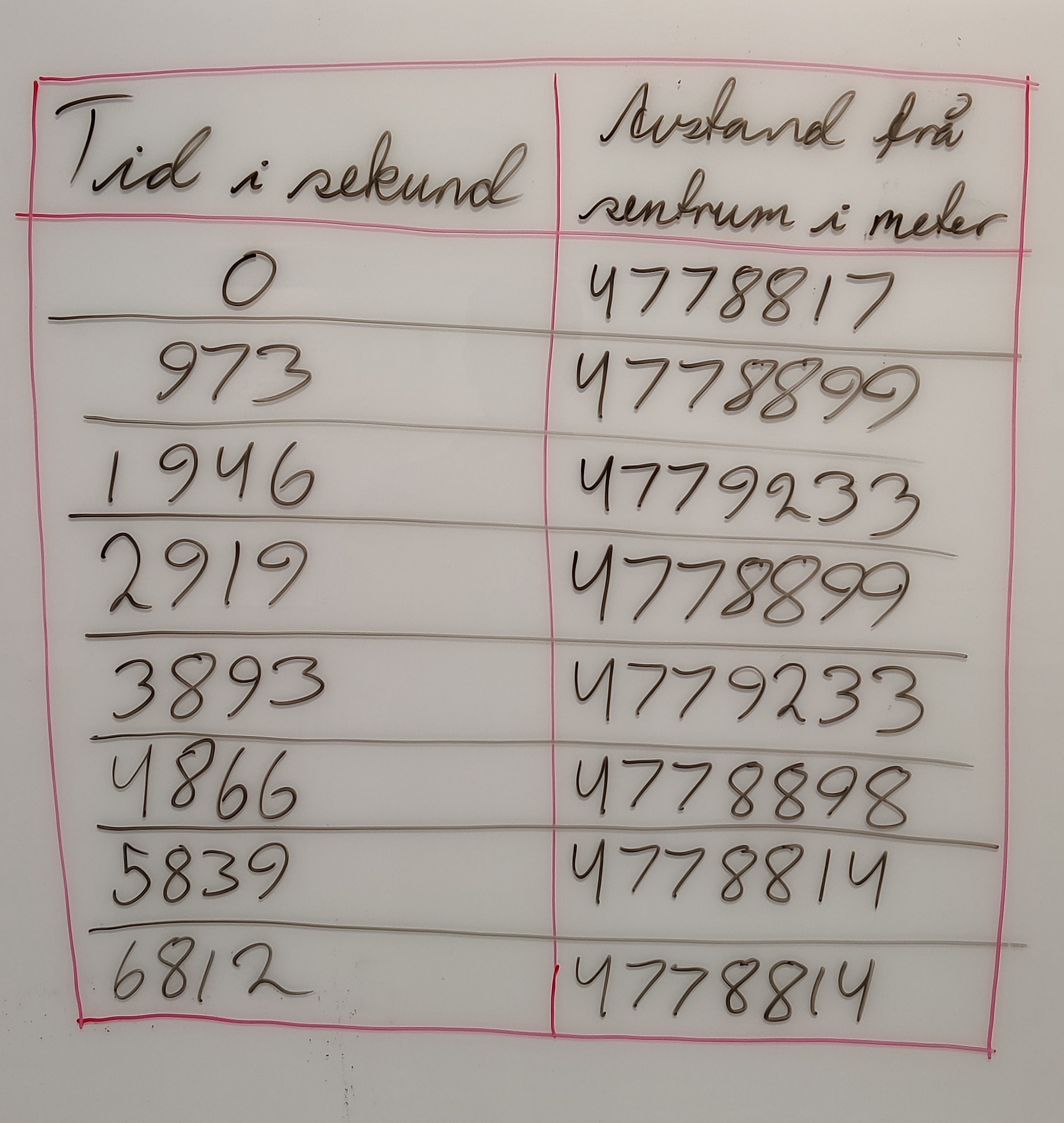
Som vi ser av målingane så er det største spriket i avstand i bana på \(4779233 - 4778814 = 419m\).
\(419m\)! Det er ei særs sirkulær bane! Dæven!
Og kva er det vi veit frå ei stabil bane? At den einaste krafta som verkar på lekamen er gravitasjonskrafta! Ein slik lekam er nemleg i fritt fall. Set vi då opp Newtons andre lov og legg inn formelen for sentripetalakselerasjon, får vi
\(\begin{align*} F_G &= m_sa \\ G\frac{M_pm_s}{r^2} &= m_s\frac{v^2_{stabil}}{r} \\ G\frac{M_p}{r} &= v^2_{stabil} \\ v_{stabil} &= \sqrt{\frac{GM_p}{r}} \end{align*}\)
Så det var der den formelen kom frå ja! Her er det altså berre gravitasjonskrafta frå Åtvekdal som påverkar Askeladden. Den er så dominerande at vi kan sjå bort ifrå krafta frå dei andre planetane og stjerna.
Men skal man kome seg lenger ned mot planeten, må man fyrst slakke ned farten litt slik at man fell inn mot planeten, for så å booste opp att farten til \(v_{stabil}\) i ynkst banehøgde. Som vi veit frå sirkulære baner så avheng radiusen av den kinetiske energien til skipet, eller rørsleenergien om du vil \(K = \frac{1}{2} mv^2\). Så for å minske rørsleenergien vår kan vi anten minske massa eller hastigheita.
"Tusling, du som har litt flesk på kroppen. Hopp ut." seier Askeladden.
"Aldri i livet! Då må du ta meg med makt." svarer Tuslingen som har lenka seg sjølv fast til masta.
Massa er ikkje så enkel å forandre på, så det er difor vi må slakke ned farten for å fyrst kome oss lenger ned.
Då er spørgesmålet: kor stor boost skal Askeladden gjere for å kome seg langt nok ned? Og kor stor boost må han gjere for å stabilisere seg når han er langt nok nede?
For å kome seg langt nok ned prøver han seg berre fram med litt forskjellige boostar i eit simuleringsprogram.
For å stabilisere bana si må Askeladden utføre ein boost, \(\vec{v}_{boost}\). Kor stor må denne boosten vere? \(\vec{v}_{stabil}\), altså den stabile hastigheita Askeladden skal ha ved ei lågare bane, kan utrykkjast ved å ta hastigheita før boosten og så plusse på boosten. Altså \(\vec{v}_{stabil} = \vec{v}_0 +\vec{v}_{boost}\). Og hastigheita før boosten veit han, det er jo \(\vec{v}_{stabil}\) ved 1000km og det er denne vi no kallar for \(\vec{v}_0\).
Ut ifrå dette kan man finne ut kor mykje man må booste med: \(\vec{v}_{boost} = \vec{v}_{stabil} - \vec{v}_0\).
"Nei no er det plutseleg kome ei vektorpil på den stabile hastigheita. Skyt meg!", ropar Askeladden hysterisk.
Slapp av Askeladden, det er berre \(v_{stabil}\) som vi viste lenger oppe, men nå med retning.
"Retning? Retning?! AAAAAAAAAAAAAAAAAAAAA"
Slapp off! Dette kan vi. Med litt spikking og skruing kjem vi fram til at \(\vec{v}_{boost} = \frac{\vec{v}_0}{|\vec{v}_0|} \sqrt{\frac{GM_p}{r}} - \vec{v}_0\). Kåt på ei utleiing? Sjå her!
Då er det berre å setja i gang med atmosfæra!
Kjelder:
- https://en.wikipedia.org/wiki/Atmosphere_of_Earth
- https://en.wikipedia.org/wiki/Earth_observation_satellite