Askeladden finner fram til at radiell forflyttning av lys i schwarzschilds romtid kan uttrykkes som formelen under:
\(\Delta r = \pm \left(1 - \frac{2M}{r}\right)\sqrt{1 -\left(1 - \frac{2M}{r}\right)\frac{(L/E)^2}{r^2}}\Delta t\) [1], hvor \(M\) representerer massen til det sorte hullet, \(r\) er avstanden fra sentrum av det sorte hullet til lyspartikkelen og \(L/E\) er angulær moment per energi.
\(r\Delta\phi = \pm\frac{L/E}{r}\left(1 - \frac{2M}{r}\right)\Delta t\) [2], vil være formelen for bevegelse i angulær retning.
Askeladden sender en lysstråle rett mot det svartehullet. Den vil dermed bevege seg kun radielt mot det sorte hullet. Angulær momentet til lyset vil da være \(L = 0\) og tangensiell bevegelse vil bli \(\Delta \phi = 0\). Radiell hastighet vil dermed kunne skrives som:
\(\frac{\Delta r}{\Delta t} = \frac{dr}{dt} = -\left(1 - \frac{2M}{r}\right)\), her gjelder de samme konstantene som i formelen over. Dette vil dessverre kun gjelde for langt-vekk observatøren.
Askeladden befinner seg inne i gravitasjonsfeltet til det sorte hullet og vil dermed regnes som en skallobservatør. Han må finne bevegelses ligningen for lys inne i dette tyngdefeltet. Likning [1] og [2] kan skrives om på formelen under med det som kalles "nedslagskonstanten" \(b = L / p\). Den forteller om forholdet mellom bevegelsesmengden til lyset og angulærmomentet.
\(\frac{dr}{dt} = \pm \left(1 - \frac{2M}{r}\right)\sqrt{1 - \left(1 - \frac{2M}{r}\right)\frac{b^2}{r^2}}\) [3], dette er fortsatt for langtvekk observatøren!
Han vet hva forholdet mellom en skallobservatørs avstand og tid er i forhold til langt-vekk observatøren og definerer det i formlene under:
\(dr = \sqrt{\left(1 - \frac{2M}{r}\right)}dr_{shell}\), er formelen for forskjellen mellom avstand.
\(dt = \frac{dt_{shell}}{\sqrt{\left(1 - \frac{2M}{r}\right)}}\), er formelen for forskjellen mellom tid for de to observatørene.
Askeladden setter inn de to forholdene i formlene over inn i formel [3] og løser for hastigheten i skallene. Han kommer fram til at det ender opp med å bli:
\(\frac{1}{b^2}\left(\frac{dr_{shell}}{dt_{shell}}\right)^2 = \frac{1}{b^2} - \frac{(1 - \frac{2M}{r})}{r^2}\) [4], dette er hastigheten som skallobservatøren måler og ser.
Han er nå interessert i hvordan det effektive potensialet kan se ut for lyset. Ser man nærmere på formel [4] over kan man se at den kan skrives på formen:
\(B\dot{\vec{x}}^2 = A + V(x)^2\), hvor \(A = B = 1/b^2\) og \(V(x)\) er det effektive potensialet. Dette gjelder også for orbital bevegelse i schwarzschild geometri.
Det effektive potensialet for lys vil dermed være gitt fra formel [4] som \(V_{eff}(r) = \sqrt{\frac{\left(1 - \frac{2M}{r}\right)}{r^2}}\).
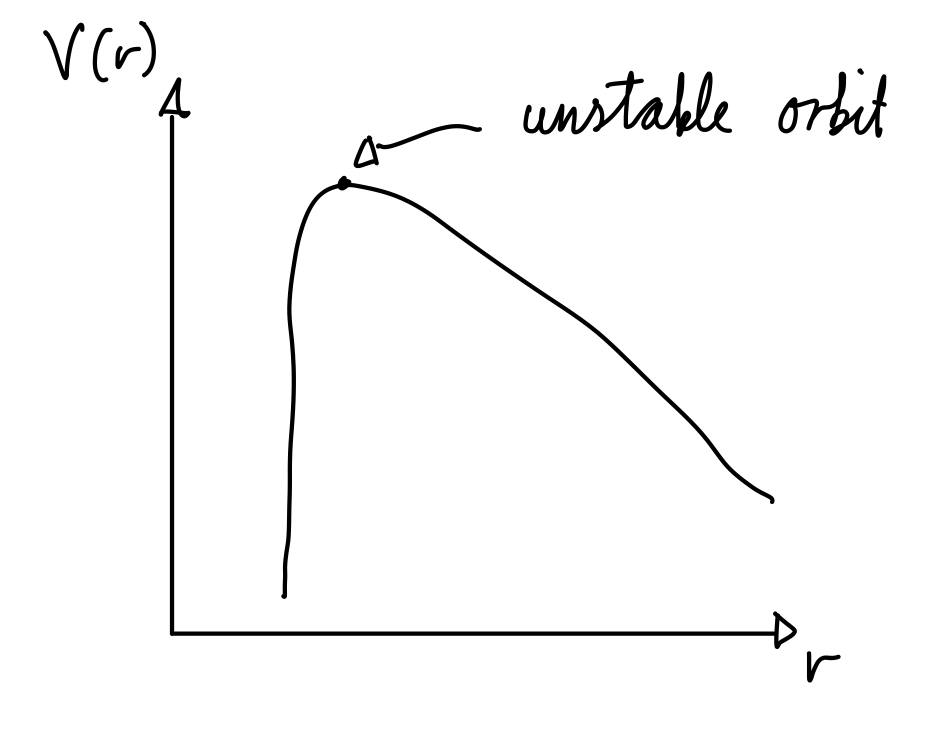
Dette potensialet kan forenkles. Askeladden setter \(2M = C\) som en konstant og skriver potensialet som \(V_{eff} = \sqrt{1 / r^2 - C/r^3}\). Deretter tegner han potensialet i figur 1. Om man tenker seg at lyset er en vogn på grafen som skal prøve å komme seg opp, må den ha høy nok kinetisk energi. Lys som ikke har høy nok energi vil komme inn mot det sorte hullet, men fare forbi. Lys som har nok energi vil bli sugd inn i det sorte hullet, men intet lys kommer til å bli fanget av det sorte hullet. Det kan oppstå en ustabil bane ved ekstremalpunktet til grafen, men det vil ikke være der lenge.
Askeladden føler seg sliten og går ned i kabinen, der finner han den gamle kisten han har glemt.