Atmosfæremodellen skal hjelpe oss, som sagt i en tidligere bloggpost, å sørge for at landingen blir så trygg som mulig. Vi vil jo nemlig ikke at raketten skal brenne opp eller at vi skal miste kontroll.
La oss nå grave oss ned i termofysikken og finne de relevante formlene for å løse dette. Vi vil så gjerne finne trykket og massetettheten gitt som en funksjon av høyden. Hva er nå uttrykket for dette?
\(P = nkT = \frac{\rho kT}{m}\)
Kanskje du har sett den før? Dette er likningen for den ideelle gassloven. Som er antakelsen vi fortsatt holder på i modelleringen. Dermed er det å relatere dette trykket til høyden som er gitt som:
\(\mathrm{d}P = -\rho(h)\cdot g(h)\cdot \mathrm{d}h\)
Dette er kjent som en differensiallikning. En differensiallikning er en likning som krever et forrige steg for å løse det neste, den må så ofte løses systematisk, med rå styrke. Vi er derimot fysikere og ikke matematikere, og har lov til å gjøre de villeste forenklinger for å komme i mål. Dette blir nok tungt å løse, men vi skal nok få resultater!
Vi gjør en antakelse at atmosfæren kan deles opp i to deler, en adiabatisk og isoterm. Adiabatisk betyr at vi har et lukket system hvor varme ikke kan komme til eller forlate systemet. Isoterm betyr det det høres ut som, en konstant temperatur. Vi antar når temperaturen blir halvparten av overflatetemperaturen, som vi fant i en forrige bloggpost, så blir atmosfæren isoterm, men nærmere overflaten er den adiabatisk.
Isoterm
La oss nå løse for en isoterm atmosfære ettersom det blir litt enklere å løse differensiallikningen med konstant temperatur. En annen antakelse vi velger å ta er at gravitasjonskonstanten er konstant, dette er mer for å ikke få et veldig stygt uttrykk for den analytiske løsningen. Vi får så:
\(\rho = \frac{PkT}{m}\)
\(\mathrm{d}P = -\frac{Pm}{kT}\cdot g\cdot \mathrm{d}h\)
\(\frac{1}{P}\mathrm{d}P = -\frac{mg}{kT}\cdot \mathrm{d}h\)
Vi gjør så dermed integralet på begge sider og får:
\(\int\frac{1}{P}\mathrm{d}P = -\frac{mg}{kT} \int \: \mathrm{d}h\)
\(\ln{P}+c_1 = -\frac{m g}{kT} + c_2\)
\(P = C_0e^{-\frac{mgh}{kT}}\)
Vi har også at skalahøyden, som er avstanden der lufttrykket avtar med en faktor \(e\) som:
\(h_0 = \frac{kT}{g m}\)
Og får så:
\(P(h) = C_0e^{-\frac{h}{h_0}}\)
Hva blir så konstanten for den generelle løsningen, vi løser for h = 0:
\(C_0 = P_0\)
Dermed blir det endelige uttrykket for den isoterme delen:
\(P(h) = P_0e^{-\frac{h}{h_0}}\)
Vi finner massetettheten som en funksjon av høyden ved å gange med \(\frac{kT}{m}\):
\(\rho(h) = \rho_0e^{-\frac{h}{h_0}}\)
Adiabatisk
For den adiabatiske delen har vi en annen likning som skal hjelpe oss å løse differensiallikningen:
\(P^{1-\gamma}T^\gamma = c\)
Hvor c er en konstant og γ er den adiabatiske indeksen. Vi antar at denne indeksen er lik 1.4 da de fleste gasser har denne indeksen. Vi kan så uttrykke den varierende temperaturen som:
\(T = c^{\frac{1}{\gamma}}P^{\frac{\gamma-1}{\gamma}}\)
Som vi kan sette inn i differensiallikningen:
\(\mathrm{d}P = -\frac{Pm}{k c^{\frac{1}{\gamma}}P^{\frac{\gamma-1}{\gamma}}}\cdot g\cdot \mathrm{d}h\)
\(\mathrm{d}P = -\frac{P^{\frac{1}{\gamma}}m}{k c^{\frac{1}{\gamma}}}\cdot g\cdot \mathrm{d}h\)
\(P^{-\frac{1}{\gamma}}\mathrm{d}P = -\frac{m}{k c^{\frac{1}{\gamma}}}\cdot g\cdot \mathrm{d}h\)
\(\int P^{-\frac{1}{\gamma}}\mathrm{d}P = -\frac{m}{k c^{\frac{1}{\gamma}}}\cdot g \int \: \mathrm{d}h\)
\(\frac{\gamma}{\gamma-1} P^{\frac{\gamma-1}{\gamma}} + c_1 = -\frac{mgh}{k c^{\frac{1}{\gamma}}} + c_2\)
\(P(h) = \left(\frac{\gamma-1}{\gamma}\cdot\left(-\frac{mgh}{k c^{\frac{1}{\gamma}}} + C\right)\right)^{\frac{\gamma}{\gamma-1}}\)
Vi finner så uttrykk for temperaturen ved å sette P tilbake inn i den adiabatiske loven:
\(T(h) = c^{\frac{1}{\gamma}}\frac{\gamma-1}{\gamma}\cdot\left(-\frac{mgh}{k c^{\frac{1}{\gamma}}} + C\right)\)
Så kan vi finne C ved å løse for h=0:
\(C = \frac{\gamma\cdot T_0}{(\gamma-1)\cdot c^{\frac{1}{\gamma}}}\)
Og da er det jo bare å bruke den ideelle gassloven for å finne massetettheten!
\(\rho(h) = \frac{kT\left(\frac{\gamma-1}{\gamma}\cdot\left(-\frac{mgh}{k c^{\frac{1}{\gamma}}} + C\right)\right)^{\frac{\gamma}{\gamma-1}}}{m}\)
Og vi har at initialverdiene er massetettheten (ρ0) ved starten av den isoterme modellen og overflatetemperaturen (T0) for den adiabatiske. Vi kan så plotte disse funksjonene for å få modellen av atmosfæren:
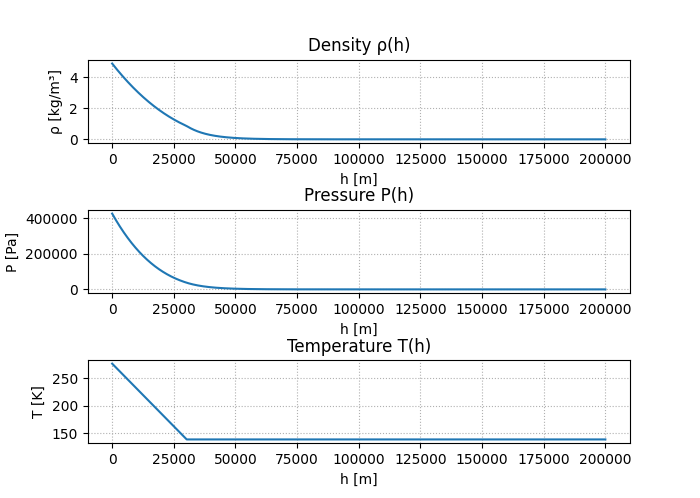
Det kan kanskje være vanskelig å se når de to modellene brukes i grafene, så her er de vist i forskjellig farge: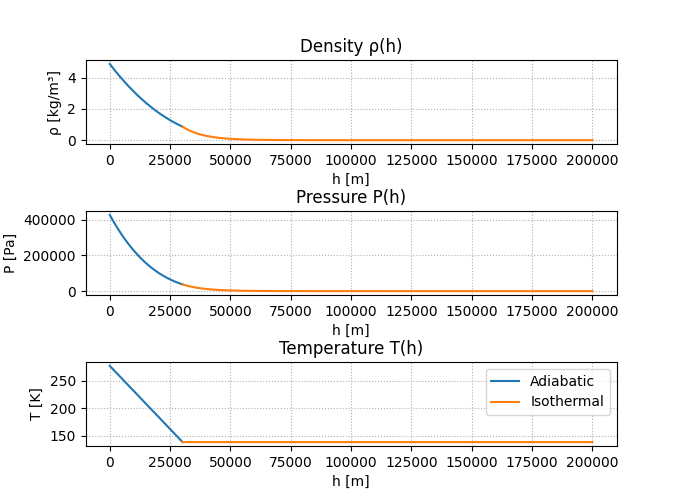
Denne modellen for atmosfæren er langt fra perfekt, vi kunne ha tatt med i antakelse at gravitasjonskonstanten endrer seg ved høyden. Det kan også godt hende at gassene vi fant i atmosfæreanalysen ga gale tall. Begge disse vil ha effekt på hvordan kurven ser ut. Det er heller ikke helt riktig å anta at atmosfæren er adiabatisk og isoterm. Disse vil også gi oss andre verdier. Allikevel, er dette en grei nok modell til å simulere atmosfæren.