Vi ser så på et foton som er på veg inn mot et svart hull. Hva blir så den målte potensielle energien til fotonet i hvert inertialsystem? Jo, vi vet fra Schwarzschildgeometrien av fra en observatør utenfor det askelererte systemet vil se farten i polarkoordinater slik:
\(\frac{\mathrm{d}r}{\mathrm{d}t} = \pm\left(1-\frac{2M}{r}\right)\sqrt{1-\left(1-\frac{2M}{r}\right)\frac{b^2}{r^2}} \\ \frac{r\mathrm{d}\phi}{\mathrm{d}t} = \pm\frac{b}{r}\left(1-\frac{2M}{r}\right)\)
Hvor så b blir støtparameteren, som ikke er verre enn distansen mellom bevegelsesvektoren og en parallell linje gjennom origo av det svarte hullet. Hvis du har lagt merke til det, vil jo lysets hastighet være 0 ved Schwarzschildradien (2M)! Vi kan så bruke dette til å finne hva farten til fotonet faktisk opplever! Nå, hvordan relaterte vi tid og distanse mellom en utenfor det akselererte systemet og en som er inni? Jo vi har fra Schwarzschild linjeelement at:
\(\Delta t_{shell} = \sqrt{1-\frac{2M}{r}}\Delta t\)
\(\Delta r_{shell} = \frac{1}{\sqrt{1-\frac{2M}{r}}}\Delta r\)
Du kan komme fram til disse ved hjelp av en del algebra, men det er ikke noe vi viser. Vi er også egentlig bare interessert i den radielle hastigheten. Den algebraen vi vil vise er derimot hvordan vi kan bruke dette til å finne den effektive potensiale energien. Vi setter inn det vi vet:
\(\left(1-\frac{2M}{r}\right)\frac{\mathrm{d}r_{shell}}{\mathrm{d}t_{shell}} = \pm\left(1-\frac{2M}{r}\right)\sqrt{1-\left(1-\frac{2M}{r}\right)\frac{b^2}{r^2}} \\ \frac{\mathrm{d}r_{shell}}{\mathrm{d}t_{shell}} = \pm\sqrt{1-\left(1-\frac{2M}{r}\right)\frac{b^2}{r^2}} = \pm\sqrt{\frac{b^2}{b^2}-\frac{b^2}{r^2}+\frac{2Mb^2}{r^3}} = \pm b\sqrt{\frac{1}{b^2}-\frac{1-\frac{2M}{r}}{r^2}} \\ \frac{1}{b}\frac{\mathrm{d}r_{shell}}{\mathrm{d}t_{shell}} = \pm \sqrt{\frac{1}{b^2}-\frac{1-\frac{2M}{r}}{r^2}} \\ \frac{1}{b^2}\left(\frac{\mathrm{d}r_{shell}}{\mathrm{d}t_{shell}}\right)^2 = \frac{1}{b^2}-\frac{1-\frac{2M}{r}}{r^2}\)
Men hvorfor skrev vi det om slik at den er opphøyd? Jo, hvis du husker fra med raketten, fant vi den effektive potensielle energien ved likningen \(A = Bv^2 + V_{eff}(r)^2\). Vi kan så nemlig se at vi kan skrive formelen vår på samme måte med \(A = B = \frac{1}{b^2}\).
\(V_{eff}(r)^2 = \frac{1-\frac{2M}{r}}{r^2} \\ V_{eff}(r) = \sqrt{\frac{1-\frac{2M}{r}}{r^2}}\)
Og da har vi løst all matematikken bak problemet! La oss så lage oss et raskt plott av denne:
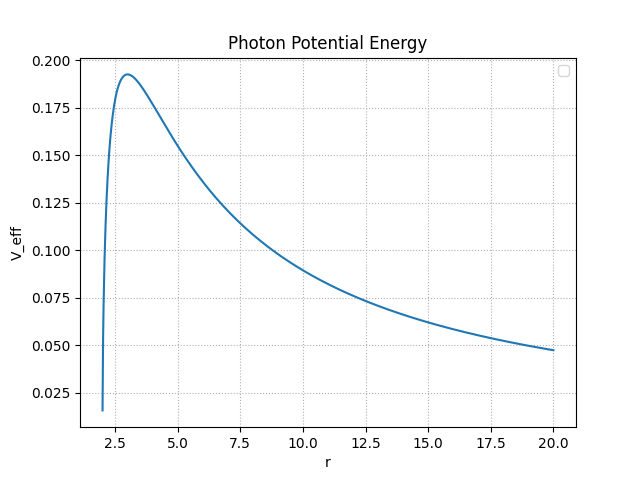
Hva forteller så plottet? Potensiell energi er jo den energien den har som kan bli kinetisk energi, så vi ser at om lyset ikke har nok potensiell energi, er det enten inn eller ut. Det eneste stedet hvor lyset kan ha en stabil bane er akkurat på toppen av kurven, men som å lage et korthus vil jo et enkelt pust sende fotonet inn mot hendelseshorisonten eller vekk.
Vi legger så merke til at lys har en annerledes form på sin effektiv potensialkurve i motsetning til materie. Dette fant vi ut ved å bruke Schwarzschild linjeelement i det vi vet om den radielle hastigheten til lys fra en observatør utenfor det akselererte systemet. Dette gjør at det blir vanskelig for lys å holde en stabil bane rundt det svarte hullet.