Det har seg sånn at jeg hadde sendt ut en satellitt for å observere et svart hull, og når jeg skulle sende den i en nærmere bane sviktet motorene! Er det mulig at satellitten min overlever?
De siste jeg vet er at den var i en bane rundt det svarte hullet på en distanse 20M fra det svarte hullet med en masse M. Tangentiellfarten var 0,993c med en vinkel på 167°. Her, la meg tegne det opp for deg.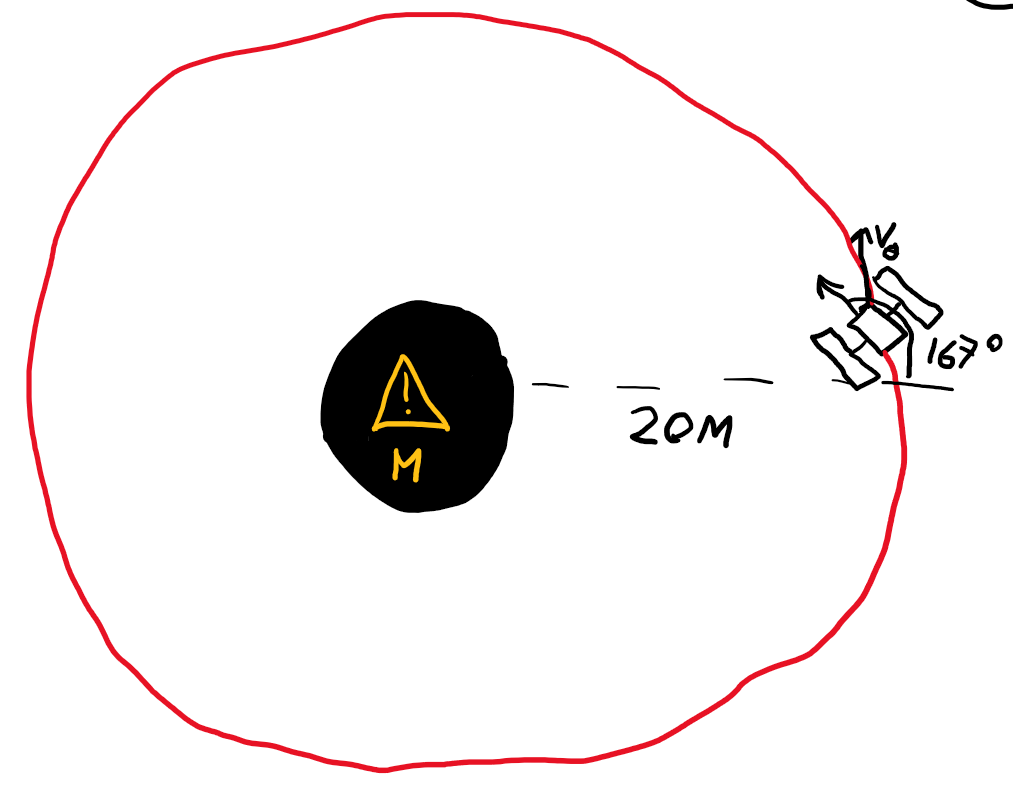
Hvordan skal vi så vite om den blir slukt eller ikke? Jo, vi vet at det så lenge vi er ikke har en stor nok effektiv potensiell energi, trenger vi ikke å være redd. Hva gjør den mer effektiv enn den vanlige potensielle energien? Effektiv potensiell energi er det å skrive den totale energien på formen \(A = Bv^2 + V_{eff}(r)\). Dette betyr at for det vanlige tilfellet vil den effektive potensielle energien være den vanlige potensielle energien, men dette skjer nødvendigvis ikke alltid:
\(V_{eff}(r) = \frac{(L/m)^2}{2r^2}-\frac{GM}{r}\)
Du ville ha kommet fram til dette uttrykket selv om du hadde delt opp hastigheten til en radiell og tangentiell, og suttet inn formelen som relaterer tangentiell hastighet og spinn! Merk også at vi har gjort energien masseløs.
Vi må derfor finne den masseløse energien. Hva var den masseløse energien definert som?
\(\frac{E}{m} = (1-\frac{2M}{r})\frac{\mathrm{d}t}{\mathrm{d}\tau}\)
Vi omskriver så \(\frac{\mathrm{d}t}{\mathrm{d}\tau} = \frac{\mathrm{d}t}{\mathrm{d}t_{shell}}\frac{\mathrm{d}t_{shell}}{\mathrm{d}\tau}\). Siden vi ser på et inertialsystem med skallet og den utenfor systemet, kan vi forenkle uttrykket slik at vi finner lorentzfaktoren. Kanskje du husker formelen for denne i en forrige bloggpost? Vi hadde jo nemlig at forholdet mellom de skulle gi lorentzfaktoren! For den siste må vi bruke Schwarzschild siden \(\tau\) er egentiden til satellitten, dette referansesystemet endrer seg hele tiden.
\(\frac{E}{m} = \sqrt{1-\frac{2M}{r}}\gamma_{shell} \\ \gamma_{shell} = \frac{1}{\sqrt{1-v_{shell}}} \\ \Delta t = \sqrt{1-\frac{2M}{r}}\Delta t_{shell}\)
Flott! Vi vil så finne ekstremalverdien for den effektive potensielle energien. Dette vil så fortelle oss hvor høy effektiv potensiell energi satellitten må ha for å bli slukt. Vi bruker formelen for effektiv potensiell energi som inkluderer relativistiske effekter:
\(V_{eff}(r) = \sqrt{(1-\frac{2M}{r})(1+(\frac{L/m}{r})^2)}\)
Slik som hvilken som helst annen vilkårlig funksjon, finner vi ekstremalpunktet hvor den deriverte er lik 0.
\((V_{eff}(r_{extremum}))' = \frac{M(3(L/m)^2+r_{extremum}^2)}{(L/m)^2r_{extremum}} = 0 \\ r_{extremum} = \frac{(L/m)^2\pm\sqrt{(L/m)^4-12(L/m)^2M^2}}{2M} = \frac{(L/m)^2}{2M}(1\pm\sqrt{1-\frac{12M^2}{(L/m)^2}})\)
Men for å løse dette må vi jo vite spinnet! Definisjonen for spinn er:
\(L = I\omega\cdot\sin{\theta}\)
Hvor treghetsmomentet (I) er gitt som det for en ring og vi omskriver vinkelhastigheten (\(\omega\)) til sin differensialform:
\(\frac{L}{m} = r^2\frac{\mathrm{d}\phi}{\mathrm{d}\tau}\)
Vi vet så at spinnet er konservert ettersom kun gravitasjonskraften fungerer på satellitten, som ikke kan påvirke spinnet.
\(r^2\frac{\mathrm{d}\phi}{\mathrm{d}\tau} = r\cdot r\frac{\mathrm{d}\phi}{\mathrm{d}t_{shell}}\cdot\frac{dt_{shell}}{d\tau}\cdot\sin{\theta} = rv_{shell}\gamma_{shell}\sin{\theta}\)
Vi gjorde så en lorentztransformasjon av vinkelhastigheten for å vite hastigheten i satellittens referansesystem.
Nå som vi har alle tallene, kan vi plotte systemet: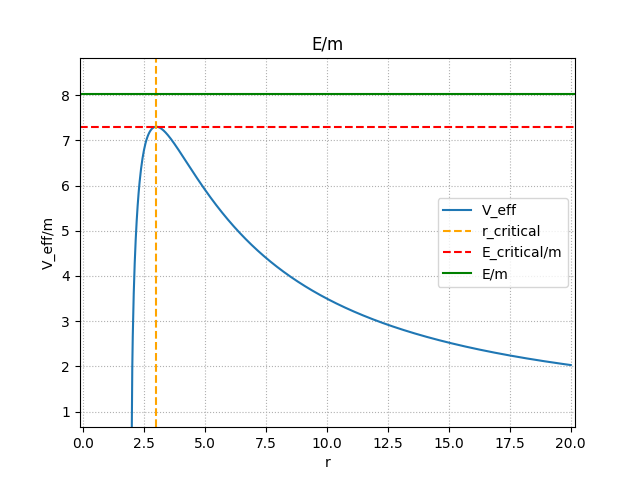
Oops... Det viser seg så at satellitten min har for mye energi og vil bli slukt av det svarte hullet med mindre det blir tilført noe energi før Schwarzschildradiusen, også kjent som event horizon. Javel, vi kan i det minste se litt nærmere på hva som vil skje med satellitten når vi kommer til event horizon, hva er tiden målt ombord? La oss si at det svarte hullet er Saggitarius A*, det kjempestore svarte hullet i midten av melkeveien. Massen dens er så \(4\cdot10^6 \mathrm{M_\bigodot}\). Vi gjør det også enklere for oss selv og sier at spinnet er lik 0.
Vi har fra Schwarzschildgeometrien at:
\(\Delta \tau^2 = \Delta s^2 = \left(1-\frac{2M}{r}\right)\Delta t^2 - \frac{\Delta r^2}{1-\frac{2M}{r}}-r^2\Delta \phi^2\)
Vi omskriver så formlene for konservert energi og spinn for å finne \(\Delta t\) og \(\Delta \phi\):
\(\frac{E}{m} = (1-\frac{2M}{r})\frac{dt}{d\tau}\\ \Delta t = \frac{E}{m(1-\frac{2M}{r})}\Delta \tau \\ \frac{L}{m} = r^2\frac{\mathrm{d}\phi}{\mathrm{d}\tau} \\ \Delta \phi = \frac{L}{mr^2}\Delta\tau\)
Som vi husker, var spinnet null og \(\Delta \phi\) blir så 0. Vi setter så inn uttrykkene og løser for \(\Delta r\).
\(\Delta \tau^2 = \left(1-\frac{2M}{r}\right) \left(\frac{E}{m(1-\frac{2M}{r})}\right)^2\Delta \tau^2 - \frac{\Delta r^2}{1-\frac{2M}{r}} \\ \Delta \tau = -\frac{1}{\sqrt{(\frac{E}{m})^2+\frac{2M}{r}-1}}\Delta r\)
Vi kan så integrere på begge sider for å regne tiden ombord. Vi vet at vi drar fra nullpunktet vårt til 2M som er hendelseshorisonten
\(\tau = \int\limits_0^{2M}-\frac{1}{\sqrt{(\frac{E}{m})^2+\frac{2M}{r}-1}}\Delta r = 0.242M\)
Vi kan så bare sette inn massen vår etter vi har endret enhet til sekund:
\(0.242\cdot4\cdot10^6\cdot M_\bigodot \frac{G}{c^3} \approx 4.76913 \mathrm{s}\)
Satellitten vil så oppleve at det har gått 4.7 sekunder. Hva skjer så egentlig med satellitten i hendelsenshorisonten? Den blir spaghettifisert, dratt ut. Dette er fordi at ved singularity går kraften som drar på satellitten mot uendelig, men siden satellitten har en lengde, vil denne kraften være annerledes mellom toppen og bunnen.
Vi ser så at det ikke er noe håp for satellitten min da den hadde for høy energi og kunne komme seg over den kritiske energien. Dette gjorde at satellitten forsvant inn i hendelseshorisonten som vi viste ville ta 4.7 sekunder på satellittens klokke ved å integrere over alle inertialsystemene til hendelseshorisonten. Satellitten blir så spaghettifisert og strekt ut til det uendelige.