Den røde og den blå raketten har endelig blitt enige om en våpenhvile, og bestemmer seg for å spille bordtennis for å feire. Som sist farer de i samme retning med konstant hastighet, men denne gangen beveger de seg i negativ x-retning. Vi står derimot nå i ro. Den røde raketten skyter en laserstråle på den blå, men den blå reflekterer denne laserstrålen tilbake. Vi observerer hendelsen fra raketten vår igjen, men fra en tryggere avstand. De to rakettene har en avstand L' mellom de. Vi har så to referansesystemer, et som følger rakettene, og et som følger raketten vår. Rakettene beveger seg med en hastighet på 0.65c i referansesystemet til romskipet vårt. Vi ser på problemet først fra rakettene sitt referansesystem. Det som blir observert er at den røde raketten skyter laseren først, så reflekter den blå raketten den. Samtidig, i dette referansesystemet, skjer det en eksplosjon om bord raketten vår. Til sist reflekterer den rød raketten laserstrålen igjen. La oss tegne opp systemet vårt og gi de navn. Vi kaller eventet hvor rød rakett skyter ut sin laserstråle for event A.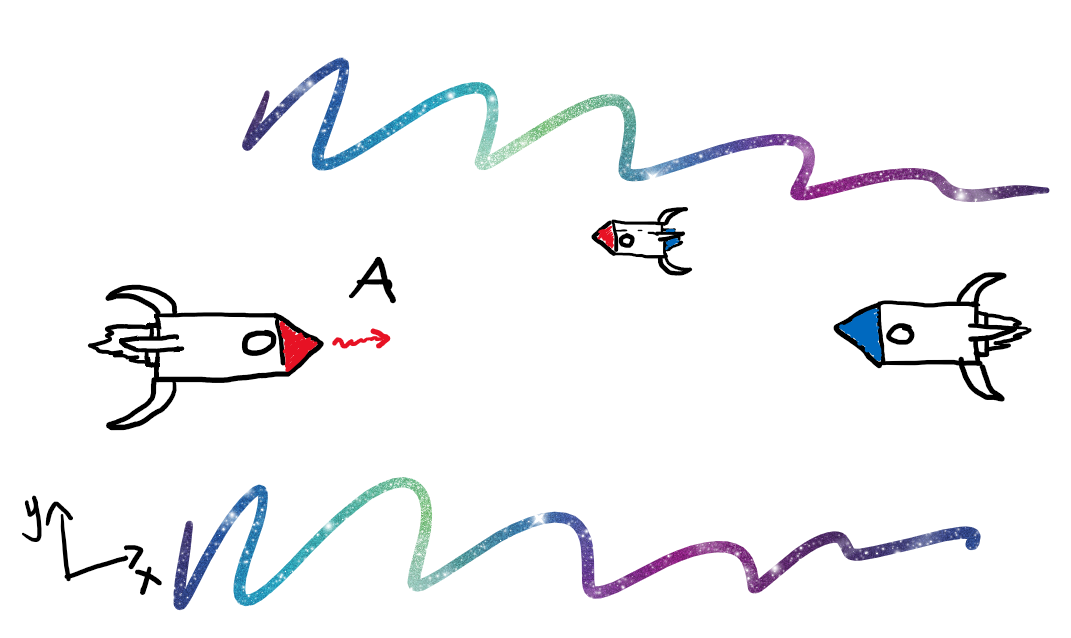 Vi kaller så eventet hvor blå rakett reflekter laserstrålen for event B, og eksplosjonen på raketten vår for event C.
Vi kaller så eventet hvor blå rakett reflekter laserstrålen for event B, og eksplosjonen på raketten vår for event C.
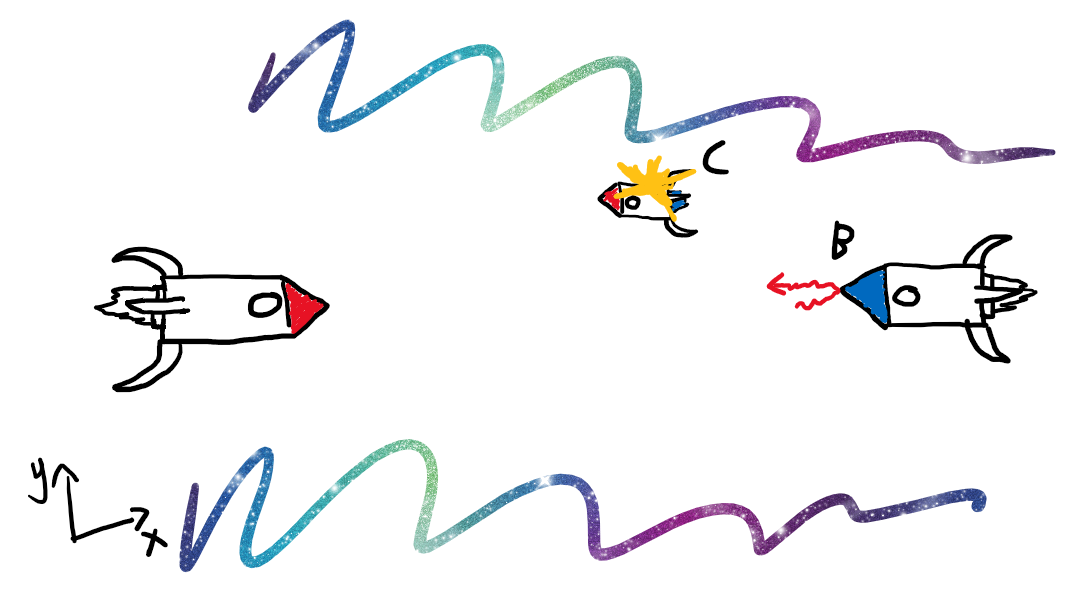
Og til sist blir at laserstrålen blir reflektert av den røde raketten igjen kalt event D.
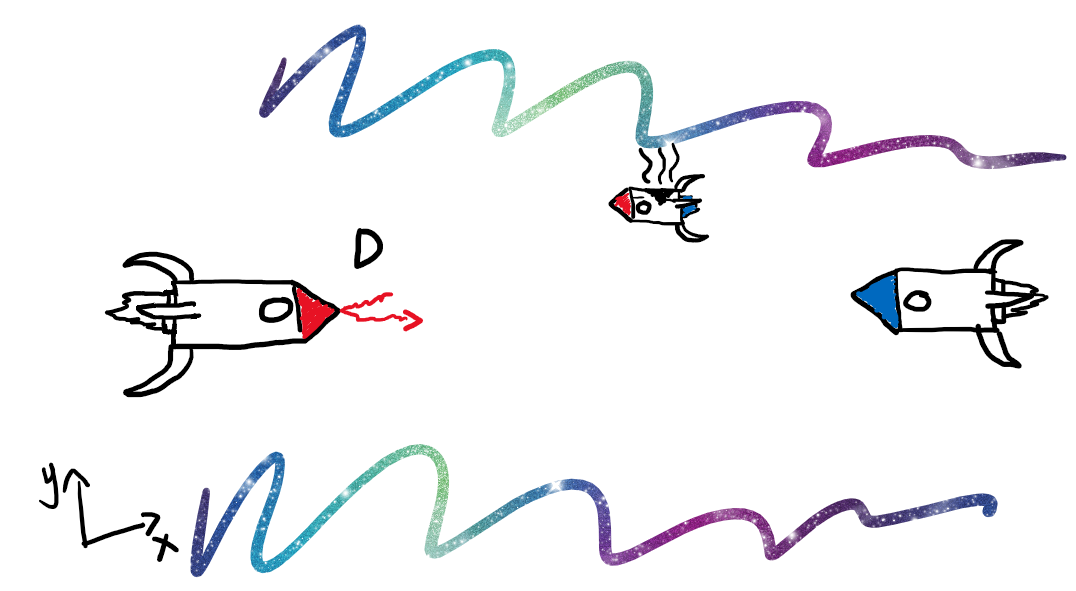
Som du kanskje husker fra forrige bloggpost, så nevnte vi at lysets hastighet er konstant i alle referansesystemer. Så fra rakettene sitt referansesystem vil så laserstrålen ta like lang tid å komme seg fram og tilbake over distansen. Tiden det tar mellom event A og B (\(\Delta t'_{AB}\)) må så være lik tiden det tar mellom event B og D (\(\Delta t'_{BD}\)).
Fra raketten vår derimot så står jo ikke rakettene i ro! Du husker jo kanskje at fra forrige bloggpost at forskjellige referansesystemer kan observere en forskjellig tid fra en annen. Det er akkurat det som vi vil observere fra raketten vår. Da vi står i ro, vil jo den blå raketten bevege seg mot laserstrålen, og det vil være en kortere distanse for lyset å gå. I motsetning vil den rød bevege seg vekk fra strålen, og det vil være en større distanse for lyset å gå. Vi kan dermed konkludere at tiden mellom
event A og B (\(\Delta t_{AB}\)) i vårt romskips referansesystem vil være mindre enn tiden mellom event B og D (\(\Delta t_{BD}\)).
La oss nå se på det samme systemet hvor vi bruker en faktisk bordtennisball istedet for en laserstråle. Rakettene beveger seg fortsatt i negativ x-retning, men nå i kun 50km/t. Bordtennisballen har alltid en konstant hastighet i rakettenes referansesystem på 80km/t. Denne bordtennisballen er i motsetning til lys ikke tvunget til å bevege seg med en konstant hastighet i alle referansesystemer. Hva ville vi så observert fra romskipet vårt?
La oss tenke over det. Den røde raketten som flyr i 50km/t observerer at ballen har en fart på 80km/t i positiv x-retning. Dette må jo bety at fra romskipet vårt som står stille, vil jo ballen kun ha en fart 30km/t. Ettersom \(80 \mathrm{km/t} - 50\mathrm{km/t} = 30\mathrm{km/t}\). Den relative hastigheten er jo gitt ved å legge sammen hastighetene fra et nullpunkt. Setter vi 80km/t som nullpunkt får vi -50km/t, som er det den røde raketten vil observere. Du kan tenke på dette som når du løper med en fart 5m/s på et tog som går 30m/s, så vil du ha en total fart fra en observatør utenfra på 35m/s.
Hva er da farten på tilbaketuren? Her flyr jo den blå raketten med bordtennisballen! For at den skal ha en konstant fart på 80km/t må den jo ha 50km/t fra nullpunktet i rakettenes referansesystem. Dermed blir det observert fra vårt romskip at ballen flyr med en hastighet på 130km/t. Siden farten er annerledes på hver veg for en observatør utenfra, vil hver referansesystem ikke være enige om bordtennisballens fart. Allikevel ser vi jo at denne økte farten vil kompensere for tiden det tok mellom de, slik at tiden mellom event A og B vil være lik tiden mellom event B og D! Dermed kan begge referansesystemene være enige om tiden.
Vi returnerer så tilbake til å bruke en laserstråle igjen, og vi har akkurat fått inn heftige data fra romtenniskampen. La oss sette opp en tabell over det vi vet:
| Rakettene | Romskipet vårt | |||
|---|---|---|---|---|
| Akse | x' (km) | t' (ms) | x (km) | t (ms) |
| A | 0 | 0 | 0 | 0 |
| B | 400 | 1.33765 | xB | tB |
| C | 260.661 | 1.33765 | 0 | tC |
| D | 0 | 2.67629 | xD = -vtD | tD |
Vi introduserer nå et konsept som alle referansesystemer kan være enige om. Tideromsavstanden er konstant. Tideromsavstanden kan tenkes på som hypotenusen på en trekant hvor hver katet er posisjon og tiden målt. Så lenge hypotenusen er konstant, kan posisjonen og tid forflytte seg fritt. Dette holder seg konsistent med det vi har observert. Det er et problem derimot. Tiderommet er ikke helt euklidisk, men har lorentzgeometri. Dette betyr bare at istedet for å legge sammen katetene og ta kvadratroten, finner vi distansen ved å trekke katetene fra hverandre. Vi kan bruke dette prinsippet til å finne tideromsdistanser for eventene fra rakettenes referansesystem, og vite at disse vil være lik i vårt romskips referansesystem. Vi skriver opp formelene for tideromsdistansen mellom event A og B i begge systemer:
\(\Delta s^2= \Delta t^2 - \Delta x^2\)
\(\Delta s'^2_{AB} = (t'_B - t'_A)^2 - (x'_B - x'_A)^2 = t'^2_B - x'^2_B \\ \Delta s^2_{AB} = (t_B - t_A)^2 - (x_B - x_A)^2 = t^2_B - x^2_B\)
Vi velger derimot å bruke naturlige enheter igjen dette betyr at vi gjør posisjonen om til lyssekunder ved \(\frac{400}{c} \approx t'_B\). I rakettenes system vil jo tiden det har tatt for laserstrålen å komme til den blå raketten være lik lyssekundene det tar. De er derfor like! Vi skriver så:
\(t'_B = x'_B\)
Dette medfører at tideromsdistansen for vårt romskips system også er 0, og vi får at:
\(t_B = x_B\)
La oss nå skrive opp tideromsdistansen for event A og C i begge systemer, her kan det lønne seg å huske at B og C skjedde simultant i rakettenes referansesystem:
\(\Delta s'^2_{AC} = (t'_C - t'_A)^2 - (x'_C - x'_A)^2 = t'^2_B - x'^2_C \\ \Delta s^2_{AC} = (t_C - t_A)^2 - (x_C - x_A)^2 = t^2_C\)
Vi setter så disse tideromsavstandene like og får:
\(t_C = \sqrt{t'^2_B-x'^2_C} \\ t_C = (\sqrt{1.33765 \mathrm{ms})^2-(\frac{260.661}{c}\cdot10^6 \mathrm{ms})^2} \approx 1.01653 \mathrm{ms}\)
Nå som vi vet nøyaktig når eksplosjonen tok sted i romskipet vårt i romskipet vårts referansesystem, er jo spørsmålet om at når den blå raketten reflekterte laserstrålen skjedde simultant med eksplosjonen i vårt system. Vi setter så opp tideromslikningene igjen og ser:
\(\Delta s'^2_{AB} = (t'_C - t'_B)^2 - (x'_C - x'_B)^2 = -(x'_C- x'_B)^2 \\ \Delta s^2_{AB} = (t_C - t_B)^2 - (x_C - x_B)^2 = (t_C-t_B)^2 - t^2_B\)
Her lønner det seg å huske hva vi hadde vist og hvilke verdier vi kjenner! Dermed setter vi de lik hverandre igjen og løser for tB som gir oss svar:
\(-(x'_C- x'_B)^2 = (t_C-t_B)^2 - t^2_B \\ t_B = \frac{x'^2_C - 2x'_Cx'_B + t_C^2 + x'^2_B}{2t_C} \\ t_B = \frac{(\frac{260.661}{c}\cdot10^6\mathrm{ms})^2-2(\frac{260.661}{c}\cdot10^6\mathrm{ms})(\frac{400}{c}\cdot10^6\mathrm{ms})+(1.01653 \mathrm{ms})^2+(\frac{400}{c}\cdot10^6\mathrm{ms})^2}{2(1.01653 \mathrm{ms})} \\ t_B = 0.614521 \mathrm{ms}\)
Vi ser så at eksplosjonen på skipet skjer etter at laserstrålen blir reflektert hos det blå romskipet! Det betyr at vi så bare har en ukjent igjen, nemlig TD. Vi velger oss tideromsavstanden fra A til D for å få de enkleste utregningene.
\(\Delta s'^2_{AD} = (t'_D - t'_A)^2 - (x'_D - x'_A)^2 = t'^2_D \\ \Delta s^2_{AD} = (t_D - t_A)^2 - (x_D - x_A)^2 = t^2_D - (-vt_D)^2 = t^2_D(1-v^2) \\\\ t^2_D(1-v^2) = t'^2_D \\ t_D = \sqrt{\frac{ t'^2_D}{1-v^2}} \\ t_D = \sqrt{\frac{(2.67679\mathrm{ms})^2}{1-0.65^2}} = 3.5224 \mathrm{ms} \\ \)
Vi kan så sette opp alle tidsintervallene for laserstrålen enkelt og greit da vi vet at i romskipets referansesystem skjer eventene i rekkefølgen A, B, C, D:
\(\Delta t_{AB} = t_B - t_A = 0.614521 \mathrm{ms} \\ \Delta t_{BD} = t_D - t_B = 3.5224 \mathrm{ms} - 0.614521 \mathrm{ms} = 2.907879 \mathrm{ms}\)
For å konkludere har vi så vist at vi kan bruke tideromsavstanden til å finne ukjente variabler i et annet referansesystem. Dette viser seg å være et av de beste verktøyene vi kan ha innenfor den spesielle relativitetsteorien til å løse problemer som kan være vanskelig å gjette seg fram til. Vi kommer fram til dette i kjernen av denne delen, nemlig tvillingparadokset!