We've looked a buch at planitary orbits and some theory of how we find out stuff about planet's masses and possibly their radius if we're lucky with the inclination. But how do we know how a star will react to a planet's orbit around it? Well, to describe this we'll be taking a few steps back and look at some of the fundamentals about orbits; known as a two body problem. Simply put, we're lookig at the two massive bodies' initial positions, masses and velocities. From this we're actually able to predict the behavior of the system in the future, since we can find the change in velocity and position as well as having the initial values of these.
In the beginning you'll be looking at the two bodies from an arbitrary origin, in a certain distance from the sun(r1) and a certain dictance from the planet(r2). Ideally we'd want to be able to look at the total distance between the two, which we will be doing, but first we need to do some maths from this origin. You see the distance between the two bosies occilates, almost like the planet was on a giant spring attatched to the star. This will allow us for make an expression of how the distance between the two as a function of time.
To start off we'll look at how this distance from our origin varies with time. Now seen as we are in space, we're actually in an environment pretty close to a vacuum, meaning we can apply Newton's 2nd law of motion for our two bodies. Since we know this we can now comfortably use Newton's second law and Newton's law of gravity to get:
\(F = G{m_1 m_2 \over r(t)^3}\vec{r(t)} = m_i \vec{\ddot{r_i}}\)
\(G \space is \space the \space gravitational \space constant, \space m_1 \space and \space m_2 \space represent \space the \space masses\)
\(r(t) = |\vec{r(t)}| which \space is \space the \space radius, \space varied \space by \space time\)
\(m_i \space represents\space mass \space nr. \space i, \space for \space example \space m_1 \space and \space m_2. \)
\(Whilst \space \vec{\ddot{r_i}} \space represents \space the \space acelleration \space of \space mass \space i \space in \space other \space words; \space a_1 \space and \space a_2\)
unless your name is Mercury which requires gravity to be viewed as an accelerated system in order to get a reasonable orbit, as newtonian mechanics work poorly when conditions become more extreme. That aside we can use this to find the force acted upon one from the other, in other words we can find the change in motion, compared to our current origin.
Next, we'll usually find the biggest guy in the solar system, which 9.9999.../10 times is the star, and we sit on it... Metaphorically, of course. We're only jellyfish after all, we can't exactly survive the increadible heat ionized hydrogen produces. In practice we're just moving the origin to the centre of this body. In this position, we're able to observe the smaller masses, wich will be orbiting us from this point, we've in other words become heliosentric purists \[T]/ Praise the sun. Our goal in doing this is finding how the total distane between the two (r), now will vary, in other words we're looking directly at the spring-like motion of the radius between the two as a function of time. Now the first step, after finding our new cozy seating position is to figure out how far away you are from the other, inferiorly sized and -heated body. Luckily we can do this with the expressions we just found with N2L and Newton's law of gravity, and some nifty use of vectors:
\(\vec{\ddot{r}} = \vec{\ddot{r_2}} - \vec{\ddot{r_1}}\)
\(We\space now \space replace \space \vec{\ddot{r_2}} \space and \space \vec{\ddot{r_2}} \space with \space G{m_1 m_2 \over r(t)^3}\vec{r}(t)= m_i \vec{\ddot{r_i}}\)
\(Giving \space us \space the \space expressions: G{m_2 \over r(t)^3}\vec{r}(t)= \vec{\ddot{r_1}} \space and \space G{m_1 \over r(t)^3}\vec{r}(t)= \vec{\ddot{r_2}}\)
\(Furthermore \space we \space place \space them \space into \space the \space same \space expression \space and \space get \space \vec{\ddot{r}}=-\frac{G}{r(t)^3}\vec{r}(t)(m_1 + m_2)\)
\(And \space finally \space we \space replace \space G(m_1 + m_2) \space with \space m \space and \space get \space \vec{\ddot{r}} = -\frac{m}{r(t)^3} \vec{r}(t) \space (*)\)
Now the next step in order to find the change in motion is pretty obvious; we need to use the formulas of motion for position, velocity and acceleration. However the deriving can be a bit tricky when we introduce unit vectors in radial and tangential directions, so I'll just plop in the formulas with a brief explanation of the variables before we race on:
\(\vec{r} = r\vec{e_r}\)
\(\vec{\dot{r}} = \vec{v} = r\vec{e_r} + r\dot{\theta}\vec{e_\theta}\)
\(\vec{\ddot{r}} = \vec{a} = ( \ddot{r}-r\dot\theta^2)\vec{e_r} + \frac{1}{r}\frac{d}{dt}(r^2\theta)\vec{e_\theta} = -\frac{m}{r^2}\vec{e_r} \space (using \space(*) \space from \space above \space with \space \frac{\vec{r(t)}}{r(t)} = \vec{e_r})\)
\(\frac{d}{dt}(r^2\theta) = 0 \space so \space this \space part \space of \space the \space expression \space dissaphears\)
\(\vec{\ddot{r}} = \ddot{r} - r\dot{\theta^2} = -\frac{m}{r^2}\)
\(Where \space \vec{\dot{r}} = v \space and \space \vec{\ddot{r}} = a \space are \space the \space single \space and \space double \space derivatives \space of \space \vec{r}\space respectively \space\)
\(\dot{\theta} \space is \space the \space derivative \space of \space the \space angle, \)
\(and \space lastly\space\vec{e_\theta}\space and \space \vec{e_r}\space are \space the \space unit \space vectors \space in \space tangential \space and \space radial \space direction \space respectively\)
Our final step before moving to the centre of mass will be to reformulate r(t) as a function of the angle r(f), by using the generalised form of Keplers 1st law:
\(r(f) = \frac{p}{1 +ecos(f)}\)
Where p = (a(1 - e2)), a being the radius of the semi major axis, e is the eccentricity of the ellipse (how wide it is) and as mentioned, f is the angle. Now on the topic of kepler

being a bit off we did touch upon his 3rd law about the orbital period being wrong and how newtonian physics corrects it, we didn't, however, go into much detail on why Kepler got this detail wrong. The short of it was weightshaming the sun; he thought the sun was soooooo, heavy the mass of the planet orbiting wouldn't impact it at all. That aside, we'll now be moving to this mysterious centre of mass we've been hyping up.
Now the centre of mass (cm) is the point where the sum of the distributed mass, here our to celestial bodies, equals 0. Because the mass of the star is much greater than that of any planet in the system, the centre of mass between the two will be within the stars radius or very close to its surface. Our first course of action here is to solve the distance from cm to each object's core, in order to have functioning tentackles I'll spare you the nitty gritty of it, but we'll be using the distance between the star and planet, which we already found, and the distribuition of mass (R):
\(\vec{R_{cm}} = \vec{0} = \frac{m_1\vec{r_{1cm}} + m_2\vec{r_{2cm}}}{m_1m_2}\), r1cm being the distance from the cm to the sun and r2cm being the distance to the planet. We'll also be using the relation between the radii: \(\vec{r} = \vec{r_2} - \vec{r_1} = \vec{r_{2cm}} - \vec{r_{1cm}} \). Doing some algebra trickery, we get:
\(\vec{r_{1cm}}=a_1\frac{1-e^2}{1+ecosf}\space , \space\vec{r_{2cm}}= a_2\frac{1-e^2}{1+ecosf}\) where we define \(a_1 = \frac{\hat{\mu}a}{m_1} \space, \space a_2 = \frac{\hat{\mu}a}{m_2}\) and \(\hat\mu = \frac{m_1m_2}{m_1 + m_2}\). Having now found the changing radius of both celestial bodies compared to cm, we are now able to look at the system's
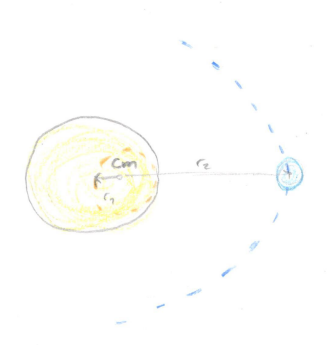
orbits from afar. Now why bother? Didn't we just change around the coordinates a little? Well you're kinda right that we only switched around the coordinates, but it gave us some critical information relating to planet observation: the star in a system orbits around a centre of mass! Now the reason we're interested in this is because it allows us to look at this mass dependence Kepler ignored, in order to observe information about planets! This is why we are able to observe the radial velocity of the star in the first place.
The final thing we'll touch on here is why the tangential velocity is isn't always 0, although we shouldn't be observing any speed from the sun. Simply put it's due to the centre of mass itself moving compared to us, this can either be due to the system having a tighter orbit around the centre of the galaxy or for some reason or another; has external forces
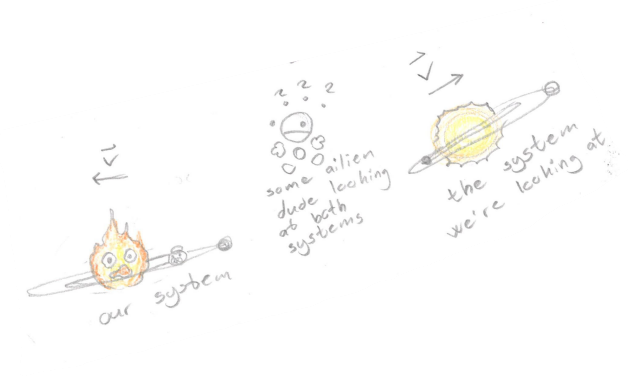
acting upon it to make it move away from- or against us. Imagine our system and the system we're observing are both contained within a sphere and the spheres themselves are moving away from or againt each other. If we try to observe anything in that sprere which should not be moving, or should have a velocity = 0, we'd need to add the system's velocity to that object, ergo it can only be 0 if we're not moving compared to the observed system.
Next we'll be having a peak at another challenge in planet observation: Spiky curves, otherwise known as noise.
