Hei igjen! Her sitter vi. Med oss har vi kaffe, snacks og all data vi har klart å samle om planetene. Masser, initialhastigheter, posisjoner og så videre. Vi har lyst til å prøve å modellere planetbanene. Dette skal vi gjøre både analytisk og numerisk. For å klare å gjennomføre en interplanetarisk reise, er det veldig nyttig å utnytte gravitasjonskrafta fra andre planeter til å slynge oss videre rundt i solsystemet. Hvis vi får det til, trenger vi kanskje ikke å ha med oss like mye drivstoff som hvis vi ikke skulle gjort det på denne måten.
Dette er en metode som har blitt brukt av blant andre NASA, for eksempel på Cassini-prosjektet. Les mer om det her: Cassini-Huygens: Operations-Gravity Assists.
Her kan dere se en ny tabell med informasjonen vi har:
| Planet | \(m_{jord}\) | \(r\) | \(x\) | \(y\) | \(v_x\) | \(v_y\) |
|---|---|---|---|---|---|---|
| 1 | \(1.431\) | \(7605.752\) | \(2.781\cdot10^8\) | \(0\) | \(0\) | \(30.483\) |
| 2 | \(1.595\) | \(7802.462\) | \(6.717\cdot10^7\) | \(-4.182\cdot10^8\) | \(24.250\) | \(4.170\) |
| 3 | \(2.762\cdot10^{-2}\) | \(1861.744\) | \(3.819\cdot10^8\) | \(3.819\cdot10^8\) | \(-17.177\) | \(14.910\) |
| 4 | \(1.579\cdot10^3\) | \(121492.1\) | \(-6.674\cdot10^8\) | \(-2.317\cdot10^8\) | \(6.689\) | \(-18.088\) |
| 5 | \(2.875\cdot10^{-2}\) | \(1956.218\) | \(3.262\cdot10^8\) | \(-1.067\cdot10^9\) | \(14,777\) | \(4.843\) |
| 6 | \(32.346\) | \(35956.421\) | \(-1.051\cdot10^9\) | \(2.419\cdot10^8\) | \(-2.448\) | \(-12.737\) |
| 7 | \(20,413\) | \(31720.534\) | \(1.398\cdot10^9\) | \(1.481\cdot10^9\) | \(-7.566\) | \(-8.401\) |
| 8 | \(1.966\cdot10^{-3}\) | \(924.481\) | \(3.171\cdot10^9\) | \(6.569\cdot10^8\) | \(-1.670\) | \(8.686\) |
Her er planetene nummerert fra 1-8, hvor 1 er den planeten nærmest stjerna, og 8 er den lengst unna. Vår hjemplanet er planet nummer 1. Beklager hvis dette blir litt mye tall, men det er her for at dere skal se hva vi har å jobbe med - og kanskje dere vil prøve selv også!
\(m_{jord}:\) massen til planeten i forhold til Jorda
\(r: \) radius til planeten, målt i km
\(x,y:\) x- og y-posisjonen til planeten, sett fra stjerna, målt i km
\(v_x,v_y:\) initialhastigheten til planeten, målt i km/s
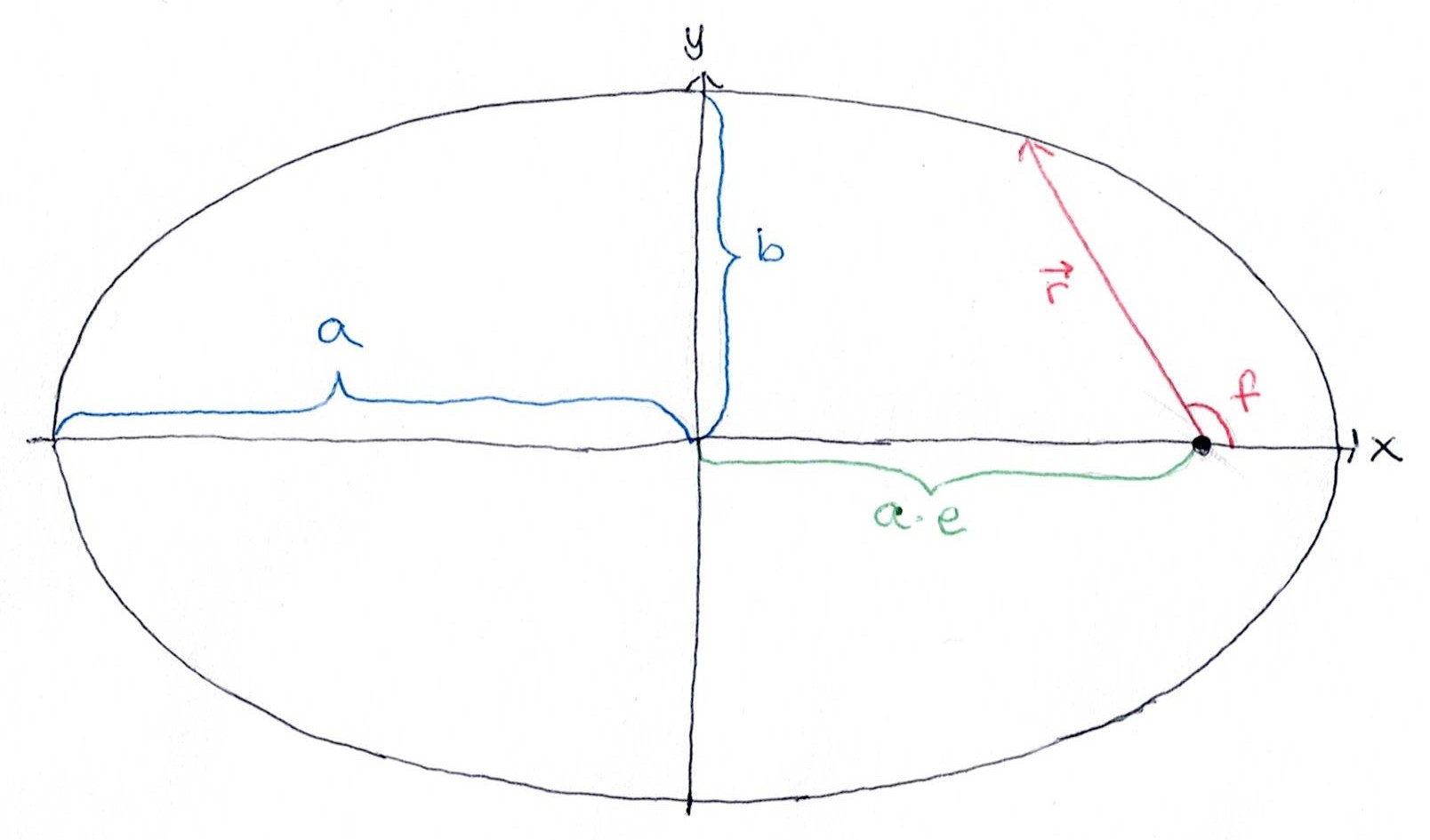
Det første vi gjør er å finne de analytiske banene. Vi setter stjerna vår i origo, og bruker formelen for ellipser. Dere kjenner kanskje til denne?
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Dette gir en ellipse med sentrum i origo, hvor \(a\) er store halvakse og \(b\) er lille halvakse. Keplers første lov sier at planetbanene følger ellipsebaner, med stjerna i det ene brennpunktet. Avstanden fra sentrum av ellipsen til det ene brennpunktet er gitt ved
\(a\cdot e\)
hvor \(e\) er eksentrisiteten. Det er et tall mellom 0 og 1, og sier i bunn og grunn noe om hvor flat etter sirkulær ellipsen er. Kan dere tenke dere hvilken form vi får dersom vi har eksentrisitet lik 0?
Formelen vi skal bruke er i polarkoordinater. Hvis du ikke husker helt hva dette er, kan du ta en titt her: wikipedia.org
Under ser dere en tabell som har alle store halvaksene og eksentrisitetene til planetene.
| Planet | Store halvakse (a) | Eksentrisitet (e) |
|---|---|---|
| 1 | \(1.85\,AU\) | \(5.6\cdot10^{-3}\) |
| 2 | \(2.78\, AU\) | \(1.7\cdot10^{-2}\) |
| 3 | \(3.63\,AU\) | \(5.2\cdot10^{-2}\) |
| 4 | \(4.77\,AU\) | \(2.3\cdot10^{-2}\) |
| 5 | \(7.75\,AU\) | \(4.3\cdot10^{-2}\) |
| 6 | \(10,00\,AU\) | \(3.4\cdot10^{-2}\) |
| 7 | \(13.56\,AU\) | \(8.4\cdot10^{-2}\) |
| 8 | \(21.12\,AU\) | \(2.9\cdot10^{-2}\) |
En ting vi kan nevne først som sist er at Jorda sin store halvakse er. *drumroll* 1! Fordi 1AU er definert til å være den gjennomsnittlige avstanden mellom Jorda og Sola. Eksentrisiteten til Jorda er \(1.7\cdot10^{-2}\).
Her er formelen for avstanden fra sentrum av en ellipse til utkanten, gitt i polare koordinater.
\(r(f)=\frac{p}{1+e\cdot cos(f)}\)
Her er \(p=a(1-e^2)\) og \(f\) er vinkelen mellom x-aksen og posisjonen på utkanten av ellipsen.
Nå er det flaks at vi har med oss en datamaskin! Vi kunne sikkert løst dette for hånd, og tegne banene på et ark, men det slipper vi! Vinkelen en hel runde rundt er \(2\pi\). Vi har
\(f\in[0,2\pi] \)
Vi deler opp intervallet i \(N\) deler, og kaller hver del \(f_i\), for \(i\in1,2,...,N\). Vi bruker \(N=101\). Det gir
\(\begin{align*} \Delta f&=\frac{2\pi}{101}\approx0.06\\ f_0&=0\\ f_1&=0.06\\ .\\.\\.\\ f_i&=f_{i-1}+\Delta f \end{align*}\)
Vi knaster disse tallene inn i datamaskinen vår. For å visualisere dette endrer vi tilbake til det vanlige koordinatsystemet (som kalles kartesisk).
\(\begin{align*} x&=r\cdot cos(f)\\ y&=r\cdot sin(f) \end{align*}\)
Det gir dette plottet:
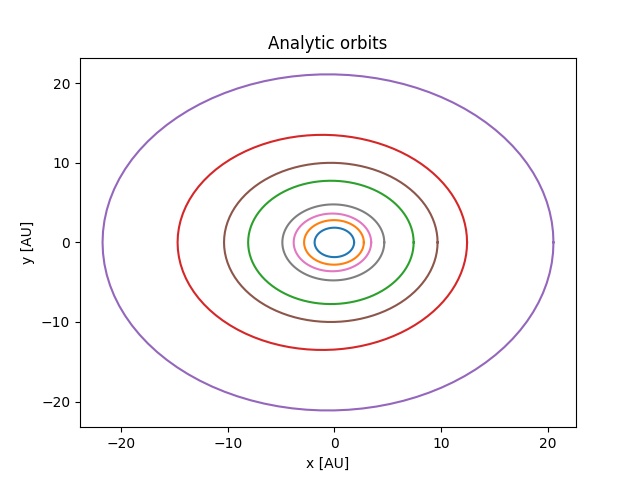
Nå kommer det en "liten" presisering. Vinkelen \(f\) er som sagt vinkelen mellom x-aksen og \(\vec{r}\). Men det er ikke hele sannheten. I det virkelige tilfellet, kan (og har) nemlig banene en forskyvning i forhold til x-aksen. Se på denne figuren:
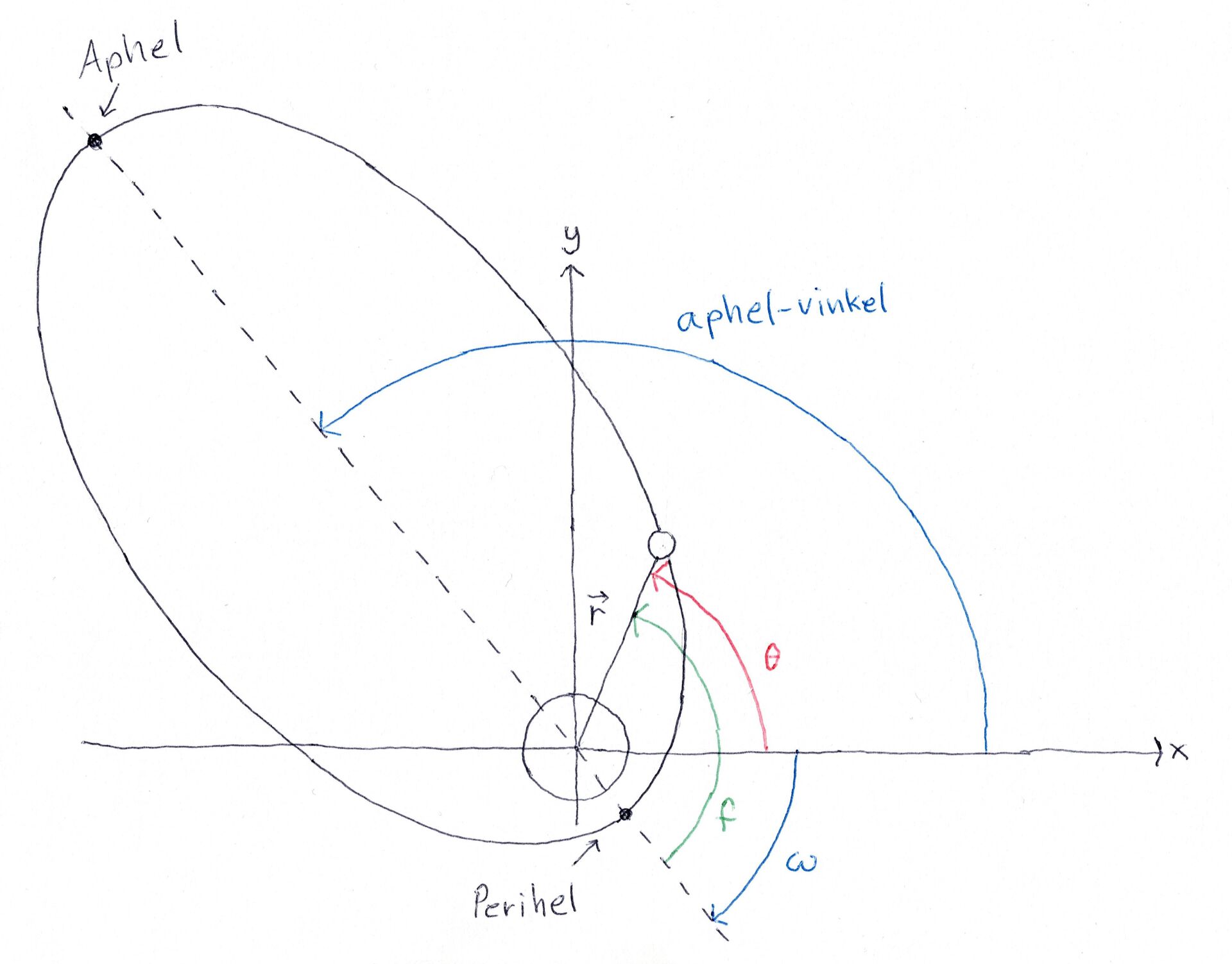
I origo ligger stjerna. Vi kaller punktet der planeten er nærmest stjerna for perihel og punktet lengst unna for aphel. Linja som mellom aphel og perihel danner en vinkel med x-aksen. Aphel-vinkel fra x-aksen til linja, og perihel-vinkel (\(\omega\)) fra x-aksen til linja. r-vektor peker fra stjerna på planeten og danner en vinkel \(\theta\) med x-aksen. Det er denne vinkelen vi er ute etter. Vi kan se at \(f=\theta-\omega\), som gir \(\theta=f+\omega\). Det gir disse nye koordinatene:
\(\begin{align*} x&=r(f)\cdot cos(\theta)\\ y&=r(f)\cdot sin(\theta) \end{align*}\)
Hvorfor har dette noe å si? Jo, dette er kun en analytisk løsning av planetbanene. La oss foregripe det neste temaet litt.
Fra tabellen over og med en god dose fysikk og programmering kan vi plotte de faktiske banene til planetene. Ettersom at de ikke nødvendigvis ligger "flatt" (\(\omega=0^{\circ}\)), vil vi ikke kunne si om banene vi har funnet numerisk stemmer overens med den analytiske løsningen. Vi skal gå nærmere inn på hvordan vi finner de numeriske planetbanene i neste innlegg, men ta en titt på hvordan plottet blir når vi ikke tar hensyn til tiltingen.
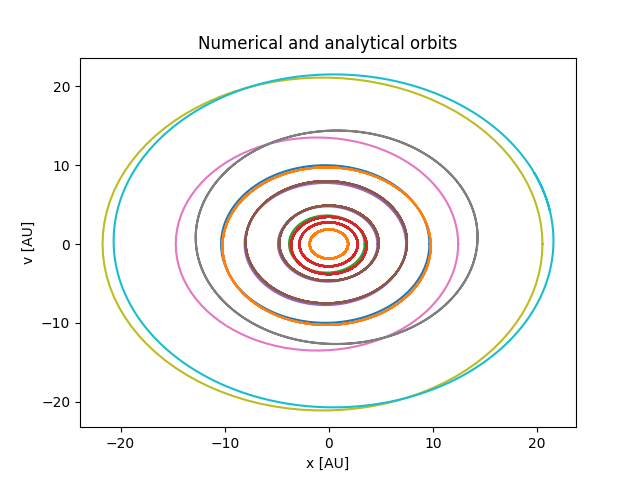
Dette ser ikke bra ut, vel? Uten å ha den kunnskapen om at banene kan være tiltet, ville enhver person tenkt at noe er galt. Grunnen til at det blir slik er at datamaskinen gjør akkurat det vi gir den beskjed om. Vi plotter den analytiske løsningen, som egentlig er tiltet, og så plotter vi den numeriske som ikke er det.
Slik ser det ut etter at vi har tatt hensyn til tiltingen:
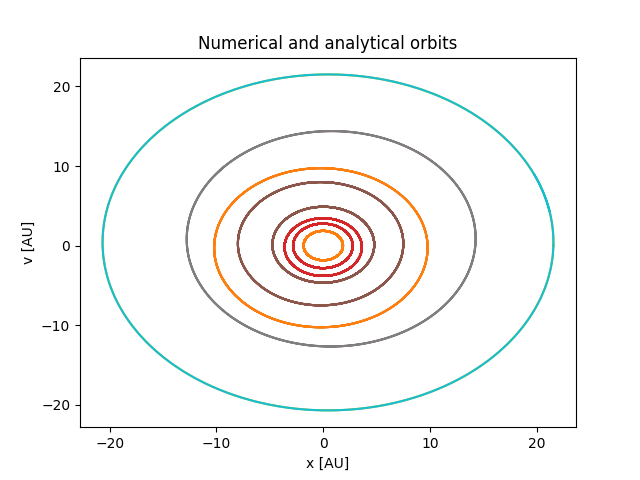
Det ser kanskje ikke sånn ut, men dette er faktisk nøyaktig det samme plottet som Figur 4, men de analytiske banene er tiltet. Det ser mye bedre ut, og vi kan slå fast at det stemmer godt overens. Det er bare å ta fram champagnen og høste ros! Eller er det så lett? Det korte svaret er nei. Vi kan ikke si noe om hvor nøyaktig dette er. Vi skal se nærmere på dette senere. I neste innlegg skal vi ta for oss hvordan vi løser dette på en datamaskin. Følg med!
