Planetbaner kommer i ulike former
Dersom du trodde at de analytiske banene vi har var nok, har jeg en dårlig nyhet.. Universet er dessverre ikke så enkelt, det hadde jo ikke vært noen utfordring for oss fysikere! Det må kraftigere lut til, vi må nemlig simulere planetbanene våre tidssteg for tidssteg.
Jeg hører at du tenker "Men har vi ikke akkurat regnet ut planetbanene med de analytiske uttrykkene? Hvorfor må vi simulere?", men frykt ikke, jeg skal oppklare: de analytiske uttrykkene gir oss riktig form på ellipsebanen, men gir oss ikke riktig posisjon på dem. Simuleringen skal gi oss posisjon av planetene som funksjon av tid, mens det analytiske uttrykket gir oss avstanden fra brennpunktet til ellipsebanen som en funksjon av vinkel. Dermed kan den analytiske banen og simulerte banen ligge rotert feil i forhold til hverandre, men fortsatt ha samme form på ellipsebanen. Sitter dette litt løst er det kanskje lurt å gå tilbake til forrige post og sjekke det analytiske uttrykket for ellipsebanen. Det kan vi fikse ved å rotere den analytiske ellipsebanen, men vi trenger fortsatt posisjonen av planeten som en funksjon av tid i stedet for vinkel. Vi er derfor nødt til å simulere det. Viktige antakelser vi også kommer til å gjøre her og i senere bloggpost er:
- Kun stjerna påvirker planetene med kraft, og planetene påvirker ikke hverandre med krefter.
- Vi ser bort ifra relativistiske effekter.
- I dette innlegget ser vi bort ifra kraften på stjerna fra de andre planetene. I en senere bloggpost skal vi se på stjernas bevegelse også.
- Vi antar at alle planetbanene ligger i samme xy-plan, og ignorerer derfor z-aksen. Da jobber vi i 2 dimensjoner.
- Alle planeter roterer om sola og z-aksen (om seg selv) mot klokka.
- Andre legemer i solsystemet (som måner) blir sett bort ifra.
Så, hvordan skal vi gå frem for å gjøre dette? Først vil jeg begynne med å si noe om hvordan vi definerer koordinatsystemet når vi simulerer, som vil være et koordinatsystem med sentrum av sola i origo, altså posisjon \((0,0)\) (slik som i Figur 1). Det betyr at simulerer vi planetbanene i et 2D-plan, xy-planet og ikke et 3D-rom. Det er kanskje greit å avklare hvor lenge vi ønsker å kjøre simuleringen vår. Vi ønsker å simulere planetbanene for minst 20 omløp av hjemplaneten, (planet 1), om sola i systemet vårt. Med andre ord må vi regne ut hjemplanetens omløpstid rundt sola i solsystemet (dette kan vi f.eks gjøre med Keplers 3. lov som vi kommer til å utlede på neste bloggpost). Dette er bare for å sørge for at vi simulerer alle planetbanene lenge nok, også tar det jo tid å reise gjennom solsystemet også tross alt. Videre trenger vi et uttrykk for akselerasjonen til hver planet. Det finner vi lett ved å bruke Newtons 2. lov. Neste steg blir å bruke en kjent teknikk for å finne posisjoner og hastigheter numerisk, numerisk integrasjon.
Som du kanskje husker, brukte vi dette da vi simulerte partikler i rakettmotoren tidligere. Det betyr at vi også blir nødt til å finne et uttrykk for akselerasjonen til hver planet. Men denne gangen møter vi på et problem: metoden vi brukte sist blir rett og slett ikke nøyaktig nok i simuleringen vi skal gjøre nå. Tidligere brukte vi noe kalt Eulers metode, som er god nok når vi ser på korte intervaller slik som i rakettmotoren, men ikke god nok i vårt tilfelle nå. I tillegg er ikke Eulers metode det vi kaller energibevarende, altså får/mister systemet energi over tid når det ikke burde det (som i Figur 2). Hva som gjør en metode energibevarende er jobb for en numeriker, så jeg tar med ikke bryet med å forklare det her, men det er likevel viktig å vite om metoden vi skal bruke har denne egenskapen. Vi kunne kanskje brukt Eulers metode's storebror, Euler-Cromer! Han er jo energibevarende! Her sparer jeg meg selv tid ved å ikke implementere det, fordi jeg vet allerede at denne metoden heller ikke er presis nok over tid..
Her trengs det andre astronomiske boller. Vi trenger mer presise, energibevarende astronomiske boller. Vi leter rundt i verktøykassa, og finner et redskap kalt leap-frog. Dette er en energibevarende og presis nok metode for numerisk integrasjon, som vi kommer til å bruke i simuleringen vår. Oppsummert + litt ekstra er dette overordnet hvordan vi løser problemet:
- Vi finner tiden til x antall omløp for hjemplaneten om sola med Keplers 3. lov, \(P^2 = \frac{4\pi^2a^3}{G(m_1 + m_2)}\) og med x som minimum 20 omløp.
- Vi finner uttrykket for akselerasjonen til planeten vi skal simulere med Newtons 2. lov, \(\Sigma\vec{F} = m\vec{a}\).
- Vi bruker data om initialposisjoner og initialhastigheter for planetene, også integrerer vi opp posisjonen og hastigheten til alle planetene i solsystemet over tid med den numeriske metoden leapfrog over tiden for 20 omløp om sola med hjemplaneten. Videre kan vi visualisere og teste dataen vi har fått.
Data for masser (planeter og stjerne), store halvakser, initialposisjoner og initialhastigheter for hver planet som vi kommer til å bruke i denne posten kan du finne på de forrige bloggpostene, Solsystemet vårt og Analytiske planetbaner, så jeg lager derfor ingen tabell i denne posten. MERK at vi i denne simuleringen kommer til å bruke enheter som AU (astronomiske enheter) for lengde, \(\odot \) (solmasser) for masse, og yr (år) for tid, som betyr at kjente konstanter som Newtons gravitasjonskonstant G eller \(\textbf{$\gamma$}\) (avhengig av hva man pleier å bruke) også vil se litt annerledes ut på grunn av enhetene. f.eks er \(G = 4\pi^2 AU^3 yr^{-2}M^{-1}\) der \(M=M_{planet} + M_{sol}\) , generelt er \(M\) total masse i banesystemet vi ser på. Vi bruker i denne oppgaven at \(M_{sol}=M\odot\) (planetmassen er liten i forhold, derav neglisjerbar), altså ikke massen til stjerna i solsystemet vårt, men en solmasse (massen til sola i jordas solsystem).
Hoppe frosk - numeriske datafrosker

Leapfrog er en metode for numerisk integrasjon, på lik linje med metoden vi har brukttidligere. Ideen med numerisk integrasjon er å regne ut hva den neste posisjonen og hastigheten er ved å gå et bittelite tidssteg videre ved å gjøre approksimasjoner. Derfor er det veldig viktig at tidssteget vårt er lite nok. Ellers blir det en dårlig approksimasjon. Andre eksempler på numerisk integrasjon er Eulers-Cromer eller Eulers metode beskrevet i et tidligere innlegg. Vi vet hvor planetene befinner seg i en tid t=0, hvilken hastighet de har der, og akselerasjonen kan vi finne med Newtons lover. Da har vi alt vi trenger for å integrere numerisk. Denne metoden er liiitt mer komplisert enn Eulers metode som vi har brukt tidligere, men kan fortsatt utledes på en enkel måte. Jeg kommer ikke til å gjøre det her, men du kan finne det i et vedlegg linket her om du er interessert. Metoden for leapfrog tar flere former, så jeg skal vise dere to av dem - og prøve å gi litt intuisjon.
\((1) \begin{align} a_i &= A(x_i) \\ v_{i+\frac{1}{2}} &= v_{i-\frac{1}{2}} + a_i\Delta t \\ x_{i+1} &= x_i + v_{i+\frac{1}{2}}\Delta t \\ \end{align}\) \((2) \begin{align} a_i &= A(x_i) \\ x_{i+1} &= x_i + v_i\Delta t + \frac{1}{2}a_i\Delta t^2 \\ a_{i+1} &= A(x_{i+1})\\v_{i+1} &= v_i + \frac{1}{2}(a_i + a_{i+1})\Delta t \end{align}\)
Hva er det som skjer i denne metoden? I stedet for å gå hele steg om gangen, tar vi et mellomsteg på hastigheten. For å illustrere hva som skjer kan vi tegne opp en linje med indeks, posisjon og fart. Posisjon vil da representeres som grønn frosk, og hastighet som rosa frosk:
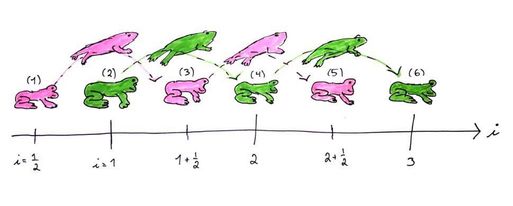
Det ser nesten ut som at leapfrog hopper bukk, og det er jo det den gjør. Leapfrog oversatt direkte til norsk er jo hoppe bukk! Illustrert på Figur 3 ser man hvordan leapfrog løper på indeksene. Nummereringen i illustrasjonen kan være litt misvisende, fordi rosa frosk er ferdig med hoppet sitt fra (1) til (3) før grønn frosk begynner å hoppe i (2), mens i illustrasjonen kan det virke som om det er motsatt. Altså blir rekkefølgen på regningen (1) til (3), (2) til (4) til (3) til (5), (4) til (6) osv. Det som er verdt å merke seg er at vi også må regne ut akselerasjonen i det neste tidssteget underveis, som er annerledes enn fra tidligere metoder vi har sett på.
I vårt tilfelle vil posisjon og hastighet være tomme arrays (litt om arrays her om du ikke husker) som inneholder initialposisjon og initialhastighet for en tid t=0 til en planet i x og y-retning, som vi fyller opp med posisjoner og hastigheter planetene vil ha med tiden ved bruk av leapfrog. For numeriske beregninger egner formel (2) for leapfrog seg bedre (lettere å implementere). Det er denne vi kommer til å bruke senere for leapfrog.
Simulate orbits - 101
Fra punktlisten ovenfor vet vi nå akkurat hva vi må gjøre. Men hvordan skal vi gjøre det? Fra punkt 1) står det at vi må finne ut hvor lenge vi skal simulere, som er minimum 20 omløp om sola for hjemplaneten vår. Vi velger 21 omløp så vi er sikre på at vi har ekstra god tid, uten at det skal ta for lang tid å simulere. Vi finner så tiden hjemplaneten bruker på ett omløp om sola, ved å bruke Keplers 3. lov som er gitt som:
\(P = \sqrt{\frac{4\pi^2a^3}{G(m_1 + m_2)}}\approx 1.8yr\)
der \(a\) er store halvakse i ellipsebanen til hjemplaneten, \(G\) er Newtons gravitasjonskonstant, \(m_1\) er massen til solen i solsystemet og \(m_2\) er massen til hjemplaneten. \(P \) er da omløpstiden til hjemplaneten vår gitt i år, på grunn av enhetene vi bruker. For å videre få tiden hjemplaneten bruker om sola 21 ganger er alt vi trenger å gjøre å gange \(P\) med 21, som gir oss total omløpstid som
\(\text{total time} = 21\cdot P\)
Nå som vi har total tid for simulering, kan vi gå videre til punkt 2), hva er akselerasjonen. Vi antar at eneste kraften som virker på en planet er kraften fra sola, og vi neglisjerer krefter en planet får fra de andre planetene i solsystemet siden de blir veldig små i forhold (tenk sola har en masse med potens \(10^{30}\) mens jorda har en masse med potens \(10^{24}\), som betyr at kraften fra sola er rundt 1 million ganger større). Dette gjør det litt enklere for oss, og kraften fra sola på en planet er gitt av Newtons gravitasjonslov:
\(\Sigma\vec{F} = m_{planet}\vec{a} = -G\frac{M_{sun}m_{planet}}{r^2}\frac{\vec{r}}{r}\)
der \(\vec{r}\)er posisjonsvektoren til planeten vi ser på som peker fra sentrum av sola til sentrum av planeten, og \(r = |\vec{r}|\). De andre størrelsene bør være trivielle. Løser vi for akselerasjonen får vi uttrykket:
\(\vec{a} = -G\frac{M_{sun}}{r^2}\frac{\vec{r}}{r}\)
MERK at akselerasjonen blir det samme for alle planetene. Det som også er verdt å merke er at akselerasjonen er avhengig av posisjonen til planeten, som betyr vi blir nødt til å oppdatere uttrykket underveis og på slutten av hver iterasjon med leapfrog.
Med data for initialbetingelser fra Solsystemet vårt og Analytiske planetbaner er vi nå klare til å anvende leapfrog og få de faktiske planetbanene som funksjon av tid. Vi velger å bruke omtrent 11000 tidssteg for hvert år vi simulerer (vi runder av til nærmeste heltall fordi desimale tiddsteg ikke gir mening), som betyr at antall tidssteg blir \(\text{timesteps}=int(\text{total time} * 11000)\). Da får vi et tidssteg \(dt\) på \(dt = \text{total time} / \text{timesteps}\), som kommer til å bli noe rundt ca. \(\frac{1}{11000}\approx 9\cdot10^{-5}\) (ikke nøyaktig med noe rundt den størrelsen).
Solsystemet simulert
Dersom vi plotter x-posisjonen og y-posisjonen fra dataen leapfrog ga oss ender vi opp med dette plottet:
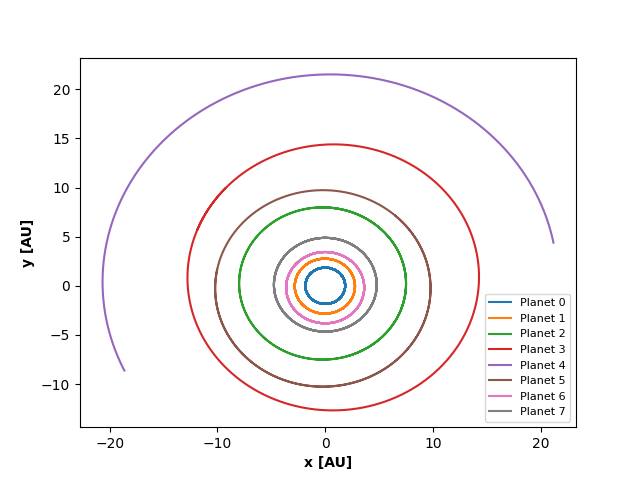
Tiden dette plottet gjelder for er 21 omløp rundt sola for planeten vår. Fra Keplers 3. lov fant vi omløpstiden til hjemplaneten vår, \(P = \sqrt{\frac{4\pi^2a^3}{G(m_1 + m_2)}} \approx1.8yr\), som betyr at tiden vi har simulert er ca. 37.8 år. Sola syntes ikke på plottet, men ville befunnet seg i origo. Banene ser lovende ut, men det er ikke bra nok for å være sikre på om det stemmer, eller hva slags baner vi har. De ser f.eks veldig sirkulære ut, men kan fortsatt være ellipser. Dette er ikke nok informasjon. Da er det kjekt å teste resultatene, og det har vi tenkt til å gjøre med Keplers lover. Men først skal vi utlede dem!