Mannen var Johannes Kepler. Han nedførte sine kjente tre lover, som lyder som følger.
- Planetenes baner er ellipser med Sola i det ene brennpunktet.
- En rett linje fra Sola til planeten sveiper over like store flater på like store tidsrom \(\left(\frac{d A}{dt}=konstant\right)\).
- Kvadratet av omløpstiden for en planet er proporsjonalt med tredje potens av dens gjennomsnittlige avstanden fra Sola \((P^2=a^3)\).
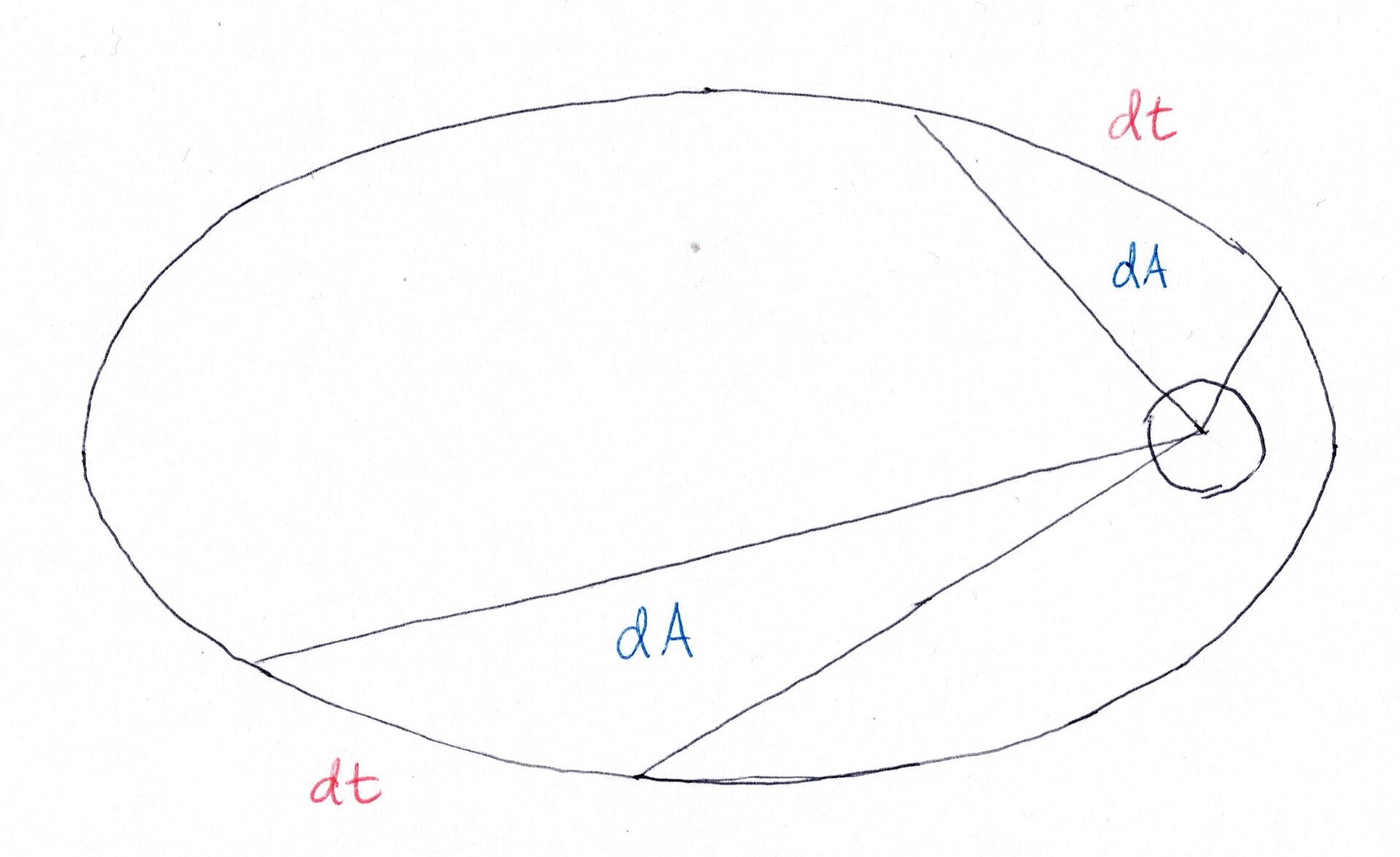
Dette er veldig nyttig for oss, for vi kan bruke disse lovene til å sjekke om våre baner stemmer. Men først må vi sjekke om Keplers lover stemmer!

Vi kunne tatt lovene forgitt, men det er ikke noe spennende. Vi ønsker jo å vite at de lovene vi bruker stemmer! La oss først ta en titt på den andre loven.
\(\frac{dA}{dt}=konstant\)
Altså vil endringen av arealet per endring av tid være konstant. Hvis vi nå ser på et infinitesimalt (uendelig lite) areal sveipet ut av en infinitesimal endring av \(r\), får vi en rettvinklet trekant.
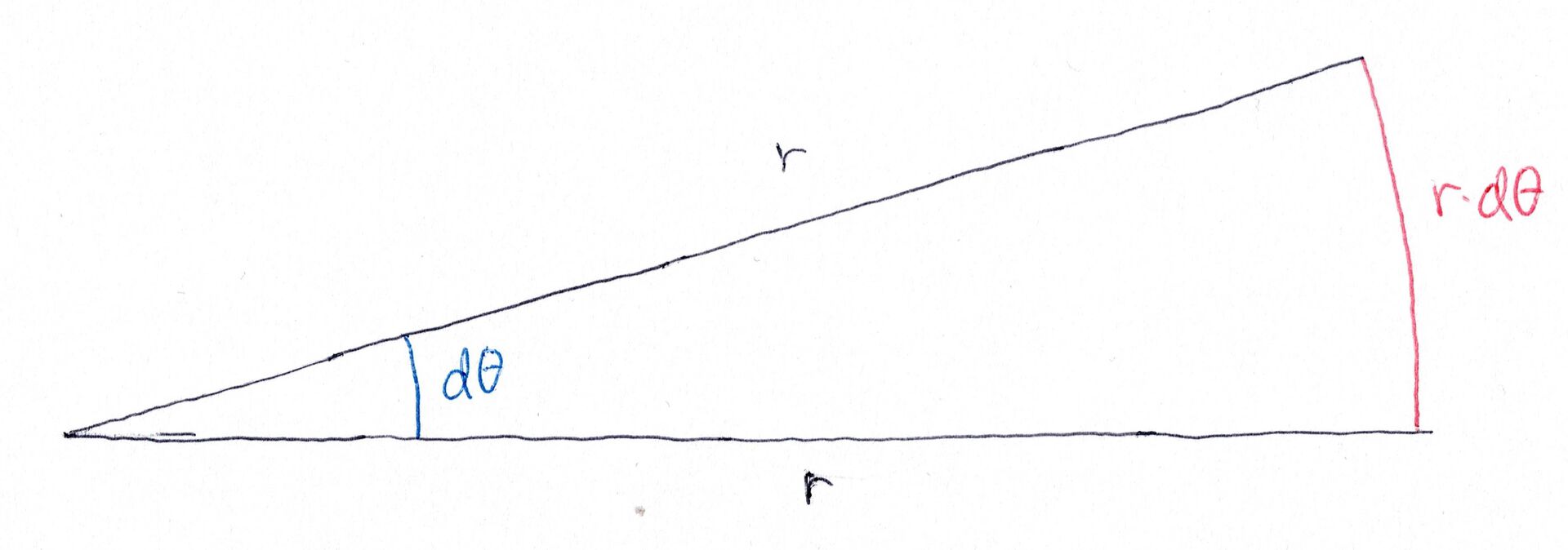
Definisjonen på en vinkel i radianer er \(v=\frac{b}{r}\), hvor \(b\) er buelengden (i rødt i Figur 2) og \(r\) er radien i sirkelen. Det gir oss at buelengden i Figur 2 blir
\(d\theta=\frac{b}{r}\\ b=rd\theta\)
Ettersom at endringen er uendelig liten, vil \(rd\theta\) bli omtrent en rett linje. Vi kan da brukte den kjente formelen for arealet av en trekant.
\(A=\frac{g\cdot h}{2}\)
hvor \(g\) er grunnlinjen, og \(h\) er høyden. Altså blir
\(dA=\frac{r\cdot rd\theta}{2}=\frac{1}{2}r^2d\theta\)
Nå skal vi innføre en ny variabel, kalt \(\vec{h}\). Den representerer spinnet til et legeme om et gitt punkt. Den er gitt ved
\(\vec{h}=\vec{r}\times d\vec{r}\)
Husk at vi opererer med polare koordinater, som gir enhetsvektorene:
\(\hat{e}_r=cos(\theta)\hat{e}_1+sin(\theta)\hat{e}_2\\ \hat{e}_\theta=-sin(\theta)\hat{e}_1+cos(\theta)\hat{e}_2\)
Hvis dere regner ut \(\vec{h}\), ser dere at det gir
\(\vec{h}=r^2\frac{d\theta}{dt}\hat{e}_z\)
Husk at \(\vec{r}=r\hat{e}_r\). Hvis dere skal derivere her, må dere huske å derivere enhetsvektorene også. Det skulle dere klare fint. Merk også at \(h=|\vec{h}|=r^2\frac{d\theta}{dt}\). Vi håper dere her ser at \(d\vec{r}=\vec{v}\). Det gir
\(\vec{h}=\vec{r}\times\vec{v}\)
Hvis vi deriverer denne en gang til, ser vi at
\(\frac{d}{dt}(\vec{r}\times\vec{v})=\frac{d\vec{r}}{dt}\times\vec{v}+\vec{r}\times\frac{d\vec{v}}{dt}\)
Dette er interessant, fordi dere husker vel at kryssproduktet av parallelle vektorer blir 0? Ser dere også at \(\frac{d\vec{r}}{dt}=\vec{v}\), som gir at kryssproduktet blir mellom to parallelle vektorer? Dermed blir det leddet 0. I det andre ledder deriverer vi hastigheten. Det gir akselerasjonen. Og siden den eneste akselerasjonen som virker her, virker radielt fra stjerna på planeten, så er denne vektoren parallell med \(\vec{r}\). Dermed blir den dobbeltderiverte av \(\vec{h}\) lik 0, og det må bety at den er konstant! Dette resultatet tar vi med oss videre.
Vi ser nå videre på Keplers 2. lov. Vi har funnet at
\(dA=\frac{1}{2}r^2d\theta\)
som altså er det lille arelalet sveipet ut av \(dr\). Hvis vi nå ser hva som skjer når vi ser på hvordan arealet endrer seg over tid, skal vi se at noe spennende kommer til å skje!
\(\begin{align*} \frac{dA}{dt}&=\frac{d}{dt}\left(\frac{1}{2}r^2d\theta\right)\\ &=\frac{1}{2}r^2\frac{d\theta}{dt} \end{align*}\)
Ser dere at vi har funnet \(h=r^2\frac{d\theta}{dt}\)? Denne vet vi er konstant, så da må altså
\(\frac{dA}{dt}=\frac{1}{2}h=konstant\)
Fantastisk! Vi har nå klart å bevise Keplers andre lov. Meget stas, klapp på skuldra!

Nå skal vi gjøre noe gøy! Vi skal nemlig bevise at Kepler tok feil. Hans 3. lov er nemlig ikke helt korrekt. Følg med nå.
Vi begynner med å kalle tiden en planet bruker på en runde helt rundt banen sin for \(P\). Videre integrerer vi alle delarealene \(\frac{dA}{dt}\) for en hel runde rundt. Vi kaller den totale flaten \(S\). Det gir
\(\begin{align*} \frac{dA}{dt}&=\frac{1}{2}h\\ \int\frac{dA}{dt}dt&=\int\frac{1}{2}h\,dt\\ \int dA&=\frac{1}{2}h\int dt\\ A=\frac{1}{2}hP \end{align*}\)
Integralet over alle delflater gir oss arealet til den flaten. Det samme gjelder integralet over alle tider, som gir oss den totale tiden. For en ellipse vet vi at arealet er gitt ved \(\pi ab\), hvor \(a\) er store halvakse og \(b\) er lille halvakse. Det gir
\(\begin{align*} \pi ab&=\frac{1}{2}hP\\ P&=2\pi\frac{ab}{h} \end{align*}\)
Nå må vi definere noen ting. Husk først formelen for en ellipse i polare koordinater:
\(r=\frac{p}{1+e\,cos(f)}\)
Dette er formelen vi presenterte tidligere. Her var \(p=\frac{h^2}{m}\), hvor \(m=\gamma(m_1+m_2)\). \(\gamma\) er Newtons gravitasjonskonstant. Men den "egentlige" formelen for en ellipse er slik:
\(r=\frac{a(1-e^2)}{1+e\,cos(f)}\)
Det vil si at \(p=a(1-e^2)\). Kjekt å vite! Vi ønsker et uttrykk for \(h\), så vi setter disse to uttrykkene like hverandre.
\(\begin{align*} \frac{h^2}{m}&=a(1-e^2)\\ h&=\sqrt{am(1-e^2)} \end{align*}\)
Nest ting er at eksentrisiteten kan skrives slik:
\(e=\sqrt{1-\left(\frac{b}{a}\right)^2}\)
Det gir oss, etter litt algebra, at \(b=a\sqrt{1-e^2}\). Husk at Keplers 3. lov sa at \(P^2=a^3\). Hvordan ser dette nå ut? Jo, se her. Vi har funnet at
\(P=2\pi\frac{ab}{h}\)
Setter vi inn de nye uttrykkene for \(b\) og \(h\) og opphøyer i andre potens, ser vi at det gir dette svaret:
\(\begin{align*} P^2&=2^2\pi^2\frac{a^2(a\sqrt{1-e^2})^2}{\left(\sqrt{am(1-e^2)}\right)^2}\\ &=4\pi^2\frac{a^4(1-e^2)}{am(1-e^2)}\\ &=4\pi^2\frac{a^3}{m} \end{align*}\)
Vi setter nå inn for \(m\), og dette er den korrekte versjonen av Keplers 2. lov. Også kalt Newtons korrekte versjon av Keplers 2. lov:
\(P^2=\frac{4\pi^2}{\gamma(m_1+m_2)}a^3\)
La oss se litt nærmere på dette. Husk fra forrige bloggpost at Newtons gravitasjonskonstant i AU-enheter er
\(\gamma=4\pi^2AU^3yr^{-2}M_{\odot}^{-1}\)
Husk også at \(M_{\odot}\) er massen til sola, og \(yr\) er år (year). La oss se på hva enhetene blir nå. For Keplers versjon har vi at \(P\) er i \(AU\) og \(a\) er i \(yr\). For Newtons versjon har vi
\(\begin{align*} P^2&=\frac{4\pi^2}{4\pi^2AU^3yr^{-2}M_{\odot}^{-1}(m_1-m_2)}AU^3\\ &=\frac{yr^2M_{\odot}}{m_1-m_2} \end{align*}\)
For å gjøre dette kort, så hadde ikke Kepler god nok data til å se at planetenes masse i forhold til Sola har noe å si. Hvis vi sier at \(m_1\) er Sola og \(m_2\) er en planet, så er Sola sin masse mye, mye større enn planeten, og \(m_1-m_2=M_{\odot}-m_2\approx M_{\odot}\). Hadde dette vært tilfellet, hadde Kepler hatt rett. Men med Newton sin rette versjon, ser vi at begge massene spiller inn. Beklager, Kepler. Newton 1, Kepler 0. I alle fall her.
Nå har vi alt vi trenger for å avgjøre hvorvidt de numeriske banene vi har kommet fram til stemmer. Det skal vi se på i neste bloggpost.
Forrige innlegg << Neste innlegg >>
