Resultat, analyse (og litt diskusjon her også)
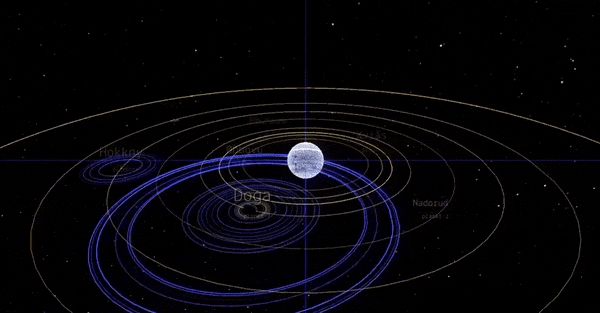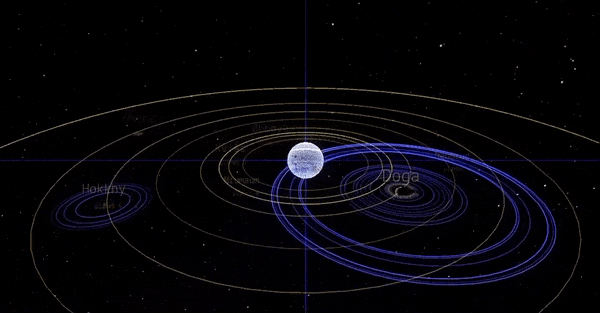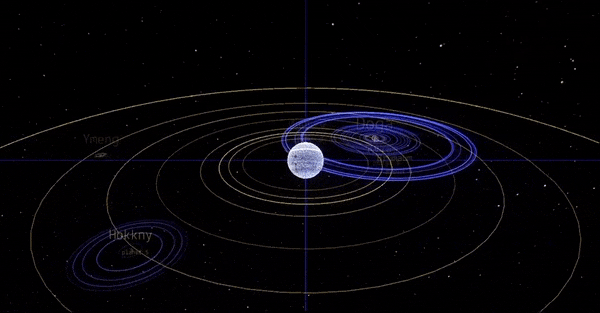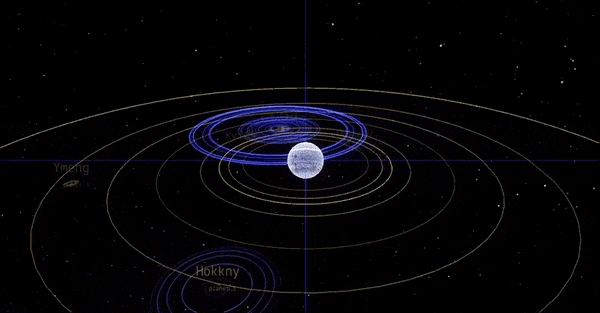
Som vist i tidligere bloggpost fikk vi dette plottet som resultat fra simulering av planetbaner:
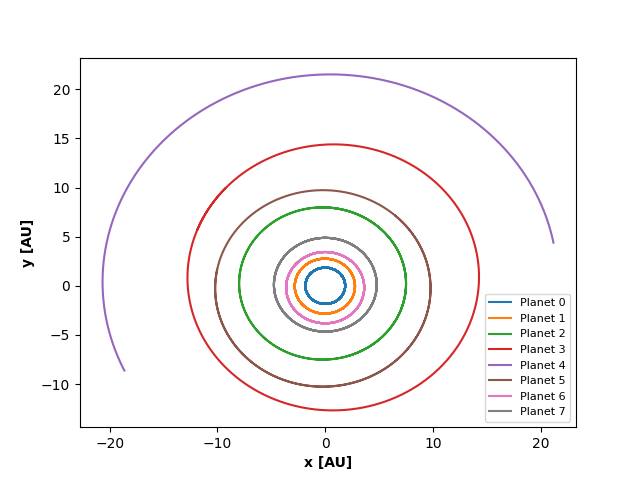
Vi kan aldri være helt sikre på resultatene våre uten å teste dem. Vi har dermed tenkt til å teste planetbanene våre med Keplers lover. Vi bruker Keplers 2. lov for å sjekke om arealet mellom 2 ulike tidsintervaller (et nært aphelium, et nært perihelium) og sjekker om de blir like, som de skal ifølge K2L (MERK at i plottet ovenfor er de numerert fra 0-7, men noen ganger er blir forskjøvet til 1-8 når vi skriver). Vi har at \(P\approx 1.8yr\) er omløpstiden for hjemplaneten (planet 0) 1 gang om solen. Da blir tidsintervallene vi har valgt \(T1 \in \left(0, \frac{P}{10}\right)\) for areal 1, og \(T2 \in \left(\frac{P}{2}, \frac{P}{2} + \frac{P}{10}\right)\), for areal 2. Tiden er valgt slik at de er ca. på motsatt side av banen, vilkårlig små men små nok til at de ikke nærmer seg hverandre så vi får effekten av at det ene arealet er nærmere aphelium og vice versa perihelium. Vi vet heller ikke hvilket av intervallene som er på aphelium eller perihelium. Regner vi ut K2L får vi følgende resultat:
| Planet | Areal 1 | Areal 2 | Relativ feil | % minst av størst verdi |
|---|---|---|---|---|
| Planet 0 | \(1.073444297m^2\) | \(1.073444338m^2\) | \(3.744527733\cdot10^{-08}\) | \(99.999996255 \%\) |
Det vi ser her er at arealene vi har fått er utrolig like. Tar vi en titt på tallene fra arealene ser vi at tallene er helt like opp til syvende desimal! Den relative feilen forteller oss også at feilen mellom de to tallene relativt til et av dem er bitte-lite! Om du ikke vet hvordan man regner relativ feil, så har vi gjort det slik: \(\frac{|A2 - A1|}{A1}\), som betyr hva forskjellen mellom de to tallene er relativt til størrelsen på et av tallene. Vi ser også at den minste av arealene er \(99.9\%\) lik den andre.
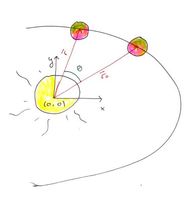
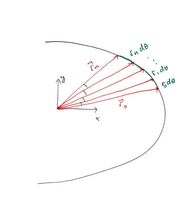
Det er også interessant å se hvor langt planeten reiste i løpet av disse to intervallene, det kan gi oss informasjon om hvor i banen vi er. Dette kan vi regne ut ved å bruke definisjonen av radianer, \(\theta = \frac{b}{r}\), der \(b\) er buelengden, \(\theta\) er vinkelen mellom vektoren som peker på startposisjonen til planeten og der den befinner seg, og \(r\) er avstanden ut til planeten. Tanken her er å gjøre \(\theta\) infinitesimalt liten, slik at vi har en \(d\theta\). Vi får dermed at \(db = rd\theta\) (Figur 3), også summerer vi opp \(db \) over hele intervallet slik at vi til slutt finner den totale lengden \(b\) planeten reiste. \(d\theta \) har vi ikke, men den kan vi finne ved at \(d\theta = \omega dt\) der \(\omega \) er vinkelfarten til planetbanen om sola, og at \(\omega = \frac{v}{r}\) der \(v\) er farten tangensialt på banen, og \(r \) er avstanden ut.
Med denne informasjonen regner vi ut hvor langt planeten reiste i hvert tidsintervall:
| Planet | Lengde reist i T1 | Lengde reist i T2 |
|---|---|---|
| Planet 0 | 1.15532914 AU | 1.16754159 AU |
| 172834780 km | 174661735 km |
Her ser vi at planeten reiser lenger i intervallet \(T2\) enn i intervallet \(T1\) (omtrent 1.8millioner km). Siden tidsintervallene er like store, betyr det at gjennomsnittsfarten i intervallet i \(T2\) må være høyere enn snittfarten i \(T1\), og derfor bør området ved \(T2\) være nær planetens aphelium. Da blir \(T1\) intervallet som ligger nær perihelium. Hang du med på det? Dette er rett og slett \(s = v\cdot \Delta t\), siden \(\Delta t \) er likt for begge intervallene må altså snittfarten være høyere i \(T2\) enn i \(T1\). Siden planeten akselererer fortere når den nærmer seg sola, vil det være der den har høyest fart i banen, og dermed tilhører \(T2 \) intervallet nærmest aphelium. Vi sjekker om dette stemmer med dataene ved å regne ut snittfarten i intervallene (vi summerer opp farten i hvert punkt og deler på antall målepunkter):
| Planet | Snittfart T1 | Snittfart T2 |
|---|---|---|
| Planet 0 | 6.428227 AU/yr | 6.496185 AU/yr |
| 109704 km/h | 110864 km/h |
Det viser seg også her som postulert tidligere at snittfarten i intervallet \(T2\) er større enn i \(T1\). Til sammenlikning har jorda en gjennomsnittlig fart i banen sin på ca. 107208km/h. Til slutt sjekker vi Keplers 3.lov og Newtons forbedret versjon. Om du ikke husker hvordan de ser ut, så kan jeg minne deg om:
\(\text{Kepler:} \;\;\;\;\; \text{Newton:} \\ P^2 \propto a^3 \;\;\;\;\; P^2 = \frac{4\pi^2a^3}{G(m_1 + m_2)}\). Vi får denne tabellen for alle planetene i solsystemet:
| Planet | Newton [yr] | Kepler [yr] | Proporsjonalitet |
|---|---|---|---|
| Planet 0 | 1.79733123 | 2.51325938 | 0.7151395725 |
| Planet 1 | 3.34764508 | 4.68110789 | 0.715139483 |
| Planet 2 | 15.43902271 | 21.58880123 | 0.715140342 |
| Planet 3 | 35.71495555 | 49.94196574 | 0.715129150 |
| Planet 5 | 22.62827914 | 31.64251724 | 0.715122598 |
| Planet 6 | 4.94618644 | 6.91638570 | 0.715140343 |
| Planet 7 | 7.45145935 | 10.43220049 | 0.714274937 |
Her ser vi at Newtons og Keplers lov stemmer godt overens. Det ser kanskje ikke sånn ut ved første øyekast, men siden konstanten \(G=4\pi^2AU^3yr^{-2}M\odot^{-1}\) så vil \(4\pi^2\) i Newtons likning forsvinne. Neglisjerer vi også planetens masse (siden den er liten ift. stjerna), og stjernas masse er ca. \(1M\odot \), så blir disse like. Her er stjerna i solsystemet omtrent på \(1.955M\odot \), så vi vil få \(P^2 = \frac{a^3}{1.955}\). Siden jeg har brukt \(P\) i tabellen i stedet for \(P^2\) kan vi for eksempel regne ut \(\frac{1}{0.715^2}\approx 1.956\), som er solmassen til sola i systemet vårt! Siden alle planetmassene er så små ift. stjernas masse blir den omtrentlig lik for alle planetene. Dermed funker Keplers tredje lov slik Kepler beskrev det, \(P^2 = a^3 \), veldig bra i et system der stjerna har masse \(1M\odot\) (MERK at om vi hadde definert masser utifra massen til stjernen vår istedet for sola så hadde Keplers lov holdt for \(P^2=a^3\) i stedet for \(P^2\propto a^3\)).
Litt mer diskusjon av resultater
1) Keplers 2. lov
Vi så tidligere i innlegget at resultatene ble gode, men ikke prikk like. Hvorfor ikke det? Jeg tror avviket i all hovedsak kommer av metoden vi har brukt, og valgt tidssteg i simuleringen. Her har vi brukt approksimasjoner som \(dA = \frac{1}{2}r^2d\theta\), der \(d\theta = \omega dt\), \(\omega = \frac{v}{r}\). Dermed kommer avviket av \(dt\) vi velger, og feilen i farten \(v\) og posisjonen \(r\) fra leapfrog-metoden. Avviket blir lite nok til at det påvirker resultatene, som jeg kommenterer nederst.
2) Lengde tilbakelagt og snittfart
På samme måte som forrige punkt tror jeg avvikene her kommer av metode og tidssteg. I tillegg til approksimasjonen i leapfrog-metoden bruker vi her approksimasjonen \(d\theta = \omega dt\) likt som før, som er bestemt av det valgte tiddsteget vi bruker, og fart og posisjon \(v,\; r\) fra den numeriske integrasjonen for \(\omega = \frac{v}{r}\).
Tidssteget vi brukte
Så lenge vi regner numerisk blir det mye tilnærminger, og derfor er det viktig med små nok intervaller slik at resultatet blir godt nok. Samtidig må vi balansere det meg regnekraft, slik at beregningstiden ikke blir for stor. Vi valgte å bruke 11 000 tidssteg pr. år vi skulle simulere, som betyr at vi hadde en \(dt\) på ca. \(\frac{1}{11000} \approx 9\cdot 10^{-5}\). Tester vi simulering med 20 000 steg og 50 000 steg tar plutselig beregningene lenger tid uten å bli noe særlig mer nøyaktig enn for simulering med 11 000 steg, og dermed bestemte vi oss for at 11 000 steg var godt nok i de beregningene vi skulle gjøre. Tidssteget er spesielt viktig fordi den inngår i nøyaktigheten av leapfrog, og 2 ganger i \(d\theta = \omega dt \) (fordi \(\omega \) bruker \(v,\;r\) som også har nøyaktighet fra metoden og \(dt\)).