Perspektiv er alt

Vi skal for det meste gjøre det veldig likt som i en tidligere post, Solsystemet på dataform, og bruker samme antakelser og metode for å gå løs på problemet.
Det er dog én vesentlig forskjell: vi må skifte koordinatsystem! Grunnen til dette er fordi at i et koordinatsystem der stjerna er sentrum i origo, vil vi ikke registrere noen bevegelse for stjernen. Setter du deg på stjernen og ser på de andre planetene, ser det ut som at kun er de som beveger seg, og at stjerna vi sitter på er helt i ro. For å registrere bevegelsen til stjernen må vi se på bevegelsen til begge legemene i et annet system. Massesenteret mellom de to legemene er et veldig bra sted å sette origo i det nye koordinatsystemet vårt, fordi det er et inertialsystem. Hva vil det si? Et inertialsystem er et system der det ikke virker noen ytre krefter på systemet, dvs. \(\Sigma \vec{F} = M\vec{A} = \vec{0}\) (der \(M\) er total masse for systemet, og \(\vec{A}\) er akselerasjonen til massesenteret). Det gjør at vi ikke trenger å tenke på noen ekstra akselerasjoner og Newtons lover er oppfylt, som gjør det enklere for oss å regne. Du kan kanskje tenke: "men akselererer ikke hele systemet et sted i universet også?". Joda, men her antar vi at ingen ytre krefter virker på systemet. Altså neglisjerer vi alle andre krefter på systemet og antar det kun er stjerna og planeten som eksisterer i dette rommet, og vi kan regne med Newtons lover. Det er veldig vanskelig å finne et ekte inertialsystem i universet (igjen, livet er ikke lett for fysikere), fordi omtrent alle systemer beveger seg. For eksempel regner vi med Newtons lover på jorda, uten å tenke på at jorda roterer. Men meteorologer kan ikke se bort i fra jordas rotasjon når de skal modellere været, for da spiller Corioliskraften en rolle. Altså er moralen her at størrelsen på systemet vi modellerer spiller en rolle. Dersom vi plasserer en ball i løse luften 10m overbakken og slipper den vil det også virke en corioliskraft, men siden den er så liten ser vi bort ifra den. Men dersom du slipper samme ball fra atmosfæren blir den plutselig mye viktigere. Samme prinsipp gjelder også andre systemer, som systemet vi skal ta en titt på nå.
Hva blir forskjellen?
Forhåpentligvis har du lest Solsystemet på dataform, fordi forskjellen blir ikke særlig stor. Metoden som blir brukt er kliss lik, så jeg kommer ikke til å ta en like nøye gjennomgang (fordi det er helt samme metode). Idéen er det samme som før:
- Vi finner ut hvor lang tid vi vil simulere med Keplers 3. lov, \(P^2 = \frac{4\pi^2a^3}{G(m_1 + m_2)}\).
- Vi finner et uttrykk for akselerasjonen med Newtons 2. lov, \(\Sigma\vec{F} = m\vec{a}\) for begge legemene vi skal se på.
- Vi setter initialbetingelser for hastighet og posisjon for begge legemene i det nye koordinatsystemet vårt og bruker leapfrog til å integrere opp hastighet og posisjon for begge legemene over hele tiden.
Så hva er forskjellen vi må gjøre? Forskjellen er at vi må flytte på initialbetingelsene slik at de er i massesenterkoordinatsystemet \(CM\) og sim-salabim så er problemet løst. Det skal jeg vise dere hvordan man gjør:
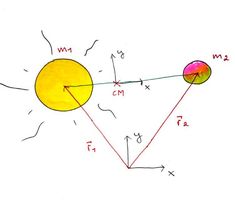
Jeg har enda ikke sagt hvordan vi finner massesenteret, men det er heldigvis ikke noe hokus-pokus. Med koordinatsystemet som har stjerna i origo vil posisjonen for massesenteret være: \(\vec{R} = \frac{m_1\vec{r}_1 + m_2\vec{r}_2}{m_1m_2}\), hvor \(m_1,\;m_2\) er massene til de to legemene, og \(\vec{r}_1,\;\vec{r}_2\) er posisjonsvektorene. Dette er et passende sted å innføre to størrelser som dukker opp mye som vi kommer til å bruke, nemlig:
\(M=m_1 + m_2\) og \(\hat{\mu} = \frac{m_1m_2}{m_1 + m_2}\). \(M\) er altså totalmassen av systemet, og \(\hat{\mu}\) er det vi kaller for den reduserte massen til systemet. Bit deg merke i disse. Det gjør at vi kan skrive opp posisjonen for massesenteret med origo i stjerne som:
\(\vec{R} = \frac{\hat{\mu}}{m_2}\vec{r}_1 + \frac{\hat{\mu}}{m_1}\vec{r}_2 = \frac{\hat{\mu}}{m_1}\vec{r}_2\) (fordi \(\vec{r}_1\) er posisjonsvektoren til stjerna ut fra origo, og stjerna ligger i origo). Deriverer vi med hensyn på tid kan vi få hastigheten til massesenteret, \(\vec{V} = \frac{\hat{\mu}}{m_2}\vec{v}_1 + \frac{\hat{\mu}}{m_1}\vec{v}_2 = \frac{\hat{\mu}}{m_1}\vec{v}_2\)
Alle vektorer som går ut fra massesenterkoordinatsystemet vil ha en \(cm\) i toppen, som f.eks \(\vec{r}_1^{cm}\), mens \(\vec{r}_1\) betyr at den går ut fra det andre vilkårlige koordinatsystemet. Det betyr at stjernas posisjon i massesenterkoordinatsystemet må være \(\vec{r}_1^{cm} = -\vec{R} = -\frac{\hat{\mu}}{m_1}\vec{r}_2\) (skjønner du hvorfor?). Jeg skal vise deg helt generelt hvordan vi oversetter dataen fra et koordinatsystem til et annet, og det er et par ting vi bør legge merke til som kan hjelpe oss senere:
- \(\vec{R}^{cm} = \frac{\hat{\mu}}{m_2}\vec{r}_1^{cm} + \frac{\hat{\mu}}{m_1}\vec{r}_2^{cm} = \vec{0}\) (posisjonen til massesenteret fra massesenterkoordinatsystemet)
- \(\vec{r} = \vec{r}_2 - \vec{r}_1 = \vec{r}_2^{cm} - \vec{r}_1^{cm} \) (1)
MERK at med likning (1) så har vi definert \(\vec{r}\) som vektoren fra legeme 1 (som kommer til å være stjerna) til legeme 2 (som kommer til å være planeten). Kanskje det kan hjelpe med en tegning for å se litt nøyere på det her:
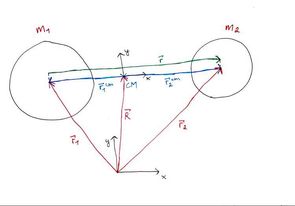
Det kan hende det er litt vanskelig å se helt på figuren, men her har vi altså to koordinatsystemer: et vilkårlig et, og et med massesenteret \(CM\) i origo. Gjennom innlegget kommer alle ting som har indeks 1, som f.eks \(m_1,\;\vec{r}_1\) etc. høre til stjernen, og alt som indekseres med 2, \(m_2, \vec{r}_2\) etc. høre til planeten. Vi lar \(\vec{r}\) være avstandsvektoren som går fra sola til planeten. Denne trenger vi for å regne ut akselerasjonen med Newtons 2. lov. For å finne posisjonene til planetene i \(CM\)-systemet kan vi se på tegningen at:
- \(\vec{r}_1^{cm} = \vec{r}_1 - \vec{R}\) og \(\vec{r}_2^{cm} = \vec{r}_2 - \vec{R}\) (2)
Vi kan finne hastighetene ved å derivere med hensyn på tid:
- \(\vec{v}_1^{cm} = \vec{v}_1 - \vec{V}\) og \(\vec{v}_2^{cm} = \vec{v}_2 - \vec{V}\) (3)
Siden vi allerede har initialverdiene \(\vec{r}_1,\;\vec{r}_2,\;\vec{v}_1,\;\vec{v}_2\) og massene \(m_1,\;m_2\) fra dataen i tabellen fra bloggpostene Solsystemet vårt og Analytiske planetbaner finner vi nå lett initialverdiene for \(\vec{r}_1^{cm},\;\vec{r}_2^{cm},\;\vec{v}_1^{cm},\;\vec{v}_2^{cm}\) med likningene i (1), (2) og (3), som vi skal kaste inn i leapfrog. Da er vi faktisk klare til å løse dette problemet. Vi må først bare bestemme et par ting til: hvilken planet skal vi simulere, og hvor lenge skal vi simulere? Vi vil helst ha en planet med stor masse og nær sola, slik at vi får størst mulig bevegelse på sola. Slår vi opp i tabellene ser vi at planet nummer 7 (det som er oppført som planet nr. 8 i tabellen i linkene ovenfor) har mye større masse enn de andre planetene, og ligger relativt nærme sola (se plott for planetbaner på tidligere post, så ser du planetbanen til planet nr. 7). Dermed er dette en veldig god kandidat. Vi velger også å simulere dette for 1 rotasjon for planet nr. 7 om stjernen, siden det er nok for å registrere bevegelsen til stjernen. For å nå løse problemet, gjør vi som jeg skrev tidligere i posten:
- Vi bruker Keplers 3. lov for å finne tiden det tar planet 7 for 1 omløp om stjerna: \(P = \sqrt{\frac{4\pi^2a^3}{G(m_1 + m_2)}}\approx 7.45yr \)
- Vi bruker nå Newtons 2. lov på begge legemene og finner akselerasjonen. Fra N2L har vi: \(\vec{F}_1 = m_1\vec{a}_1 = G\frac{m_1m_2}{r^2}\frac{\vec{r}}{r}\) og \(\vec{F}_2 = m_2\vec{a}_2 = -G\frac{m_1m_2}{r^2}\frac{\vec{r}}{r}\). Dette gir oss: \(\vec{a}_1 = G\frac{m_2}{r^2}\frac{\vec{r}}{r}\) og \( \vec{a}_2 = G\frac{m_1}{r^2}\frac{\vec{r}}{r}\), der \(r=|\vec{r}|\). Fra likning (1) har vi at \(\vec{r} = \vec{r}_2^{cm} - \vec{r}_1^{cm}\), som vi kommer til å bruke i løkken for leapfrog når vi trenger \(\vec{r}\) i akselerasjonen. Husk at alt som er indeksert med 1 er for stjerna, og 2 for planet nr. 7.
- Vi bruker likningene fra (2) og (3) til å finne initialbetingelsene, og setter dem i leapfrog. Jeg minner om at jeg ikke går i detalj på leapfrog, siden det er gjort i tidligere bloggpost. Vi kjører med samme antall tiddsteg og \(dt\) i denne simuleringen også, siden den er god nok og regneeffektiv.
På tide å kjøre kode!
Solas vals med planet 7
Etter å ha kjørt kode, plotter vi dataen av banene vi får og ender opp med dette resultatet:
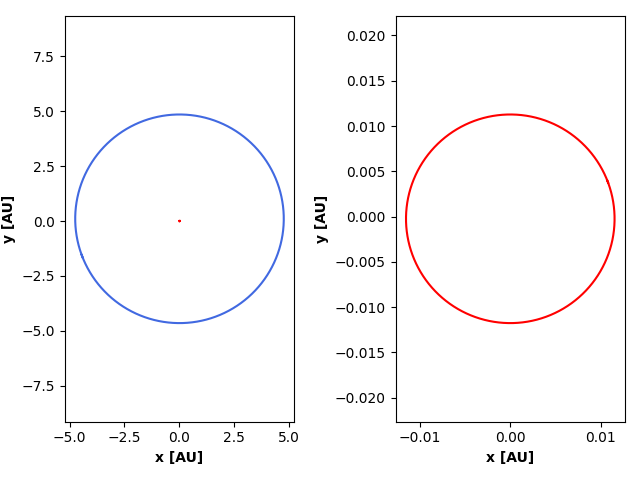
Vi har fått bevegelse for stjerna, og det liker vi. Banen til stjerna er så liten i forhold til banen for planet 7, så i plottet til høyre er kun banen for stjerna plottet slik at vi kan se bevegelsen for stjerna litt tydeligere også. Vi ser at stjerna beveger seg i en bane som strekker seg ut omtrent 0.01AU, som er omtrentlig 1.5 million km om massesenteret i systemet! For å teste nøyaktigheten av resultatene kunne vi brukt Keplers 2. lov en gang til, men det kan fort bli kjedelig. I stedet utleder jeg en likning for energien i systemet sett fra massesenterkoordinatsystemet, og bruker den istedet. Vi vet at den totale energien i et system kan skrives om:
\(E_{tot} = E_{tot,k} + E_{tot,p}\). Det betyr at vi må finne uttrykk for den totale kinetiske energien, og den totale potensielle energien. Vi kan starte med førstnevnte:
\(E_{tot,k} = E_{1,k} + E_{2,k} = \frac{1}{2}m_1v_{1,cm}^2 + \frac{1}{2}m_2v_{2,cm}^2\).
Vi trenger uttrykk for farten \(v_{1,cm}\) og \(v_{2,cm}\). Husker du tidligere, så fant vi at:
- \(\vec{R}^{cm} = \frac{\hat{\mu}}{m_2}\vec{r}_1^{cm} + \frac{\hat{\mu}}{m_1}\vec{r}_2^{cm} = \vec{0}\)
- \(\vec{r} = \vec{r}_2 - \vec{r}_1 = \vec{r}_2^{cm} - \vec{r}_1^{cm} \)
Løser vi dette likningsystemet får vi at:
\(\vec{r}_1^{cm} = -\frac{\hat{\mu}}{m_1}\vec{r}\) og \(\vec{r}_2^{cm} = \frac{\hat{\mu}}{m_2}\vec{r}\). Deriverer vi disse uttrykkene med hensyn på tid får vi:
\(\vec{v}_1^{cm} = -\frac{\hat{\mu}}{m_1}\vec{v}\) og \(\vec{v}_2^{cm} = \frac{\hat{\mu}}{m_2}\vec{v}\), som gir oss at \(v_{1,cm}^2 = |\vec{v}_1^{cm}|^2 = \left(\frac{\hat{\mu}}{m_1}v\right)^2\) og \(v_{2,cm}^2 = |\vec{v}_2^{cm}|^2 = \left(\frac{\hat{\mu}}{m_2}v\right)^2\). Setter vi dette inn i likningen for total kinetisk energi ovenfor og gjør litt algebra ender vi opp med at \(E_{tot,k} = \frac{1}{2}\hat{\mu}v^2\). Så er det potensiell energi:
Total potensiell energi for et system er gitt som \(E_{tot,p} = -G\frac{m_1m_2}{r}\). Det som er viktig å tenke på her er at potensiell energi alltid er definert ut ifra et referanse-punkt. Det betyr at vi ikke kan splitte opp potensiell energi i et uttrykk for hver av planetene, siden potensiell energi kun gir mening dersom vi ser på hele systemet samlet. Dermed er uttrykket for total potensiell energi ovenfor den totale potensiale energien i vårt system også. Vi kan gjøre en liten omskriving for \(m_1m_2 = \hat{\mu}(m_1 + m_2) = \hat{\mu}M\), og total potensiell energi blir \(E_{tot,p} = -\frac{GM\hat{\mu}}{r}\). Da blir den totale energien i systemet:
\(E_{tot} = \frac{1}{2}\hat{\mu}v^2 - \frac{GM\hat{\mu}}{r}\). Dette uttrykket bruker vi for å sjekke den totale energien i systemet vårt. Vi lager to nye arrays i leapfrog, og regner ut kinetisk, potensiell og total energi i hvert tidspunkt med integrasjonsløkken, og får plottet energien:
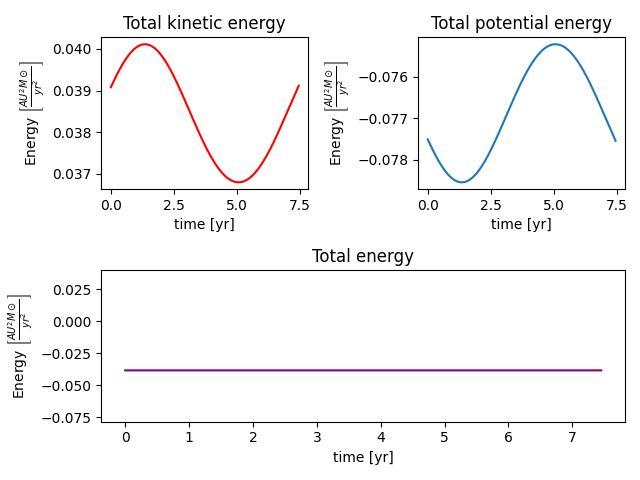
Plottet ser ganske lovende ut. Den totale energien er konstant, som er godt å se siden den skal være bevart. Kinetisk energi svinger opp når potensiell energi svinger ned, og vice versa. Det som kan være interessant å se på er at den totale energien i systemet er negativ. Jeg kommer ikke til å utlede dette, men man kan vise at dersom den totale energien i et slikt system er negativt, går planetene i ellipsebaner! (og dersom total energi \(E_{tot} = 0\) har vi sirkelbaner). Som en bonus skal jeg også vise hvordan man kan skrive det totale angulære momentet til systemet. Angulært moment er definert som \(\vec{P} = \vec{r}\times\vec{p}\) der \(\vec{r}\) er posisjonsvektoren til legemet vi ser på og \(\vec{p}\) er bevegelsesmengden. Vi regner totalt angulært moment av systemet sett fra massesenteret:
Vi kan skrive det totale angulære momentet i systemet ved hjelp av superposisjonsprinsippet: \(\vec{P}_{tot} = \vec{P}_1 + \vec{P}_2\). Vi kan videre fomulere uttrykkene som:
\(\vec{P}_1 = \vec{r}_1^{cm}\times m_1\vec{v}_1^{cm}\) og \(\vec{P}_2 = \vec{r}_2^{cm}\times m_2\vec{v}_2^{cm}\). Tidligere fant vi at:
\(\vec{r}_1^{cm} = -\frac{\hat{\mu}}{m_1}\vec{r},\; \vec{r}_2^{cm} = \frac{\hat{\mu}}{m_2}\vec{r},\; \vec{v}_1^{cm} = -\frac{\hat{\mu}}{m_1}\vec{v},\; \vec{v}_2^{cm} = \frac{\hat{\mu}}{m_2}\vec{v}\). Kaster vi disse uttrykkene inn i \(\vec{P}_1\) og \(\vec{P}_2\) og gjør litt algebra ender vi opp med dette uttrykket for total angulær moment:
\(\vec{P}_{tot} = \vec{r}\times\hat{\mu}\vec{v}\). Det som er kult å se er at uttrykkene for total energi og angulær moment sett fra massesenteret ser nesten helt like ut som de gjør til vanlig, med massen erstattet med redusert masse \(\hat{\mu}\) og total masse \(M\).
Diskusjon av resultater
Nøyaktighet av resultater kommer av valgt tidssteg og metode. Ved å velge flere tiddsteg og mindre \(dt\) kan vi få mer nøyaktige svar (opp til et visst punkt), men det går utover regneeffektiviteten. Dette er allerede kommentert i posten Solsystemet på dataform, og siden metoden vi bruker her er kliss lik med unntak av skifte i koordinatsystem vil jeg ikke gjenta det. Det ligger alltid en usikkerhet fra numeriske integrasjonsmetoder. Hvis du husker fra tidligere er det blitt nevnt at leapfrog er en energibevarende metode, og som vi så var energien i systemet bevart. Eller var den det? La oss se på et plott der jeg zoomer helt inn på kurven for total energi:
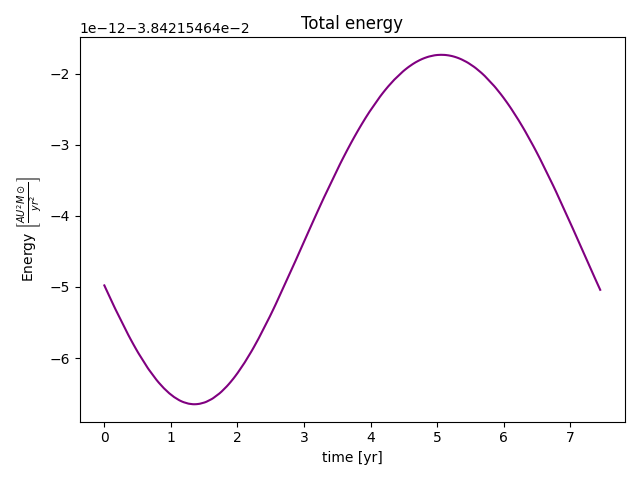
Hva er det som foregår her? Er ikke leapfrog energibevarende likevel? Jeg er ingen ekspert på numerikk (jeg er fysiker, ikke numeriker), men legg merke til størrelsesordenen på y-aksen: merkelig, sant? Når vi gjør ting numerisk vil det alltid ligge en feil fra datamaskinen også. Maskinen har begrenset med ressurser, og vil dermed alltid introdusere en slags feil. Her er feilen (uansett hvor den kommer ifra) så liten at vi kan se bort fra den. I det større bildet er energien bevart i systemet, og metoden er helt i orden. Dette er data jeg stoler på, og dermed sender vi det av gårde til forskergruppen som trengte dem. Samtidig mottar vi data fra et liknende system som vi har analysert nå, og ser hva slags spennende resultater vi kan komme frem til!