Bildet over er hentet fra furman.edu.
Når en forsker får inn data fra en stjernes hastighet, er det ikke rett fram å lese av hva hastigheten er. Se for dere at vi har rettet et teleskop mot en stjerne. Den går i bane rundt et massesenter med en planet. Men hele systemet beveger seg også. Det kaller vi egenhastigheten til systemet.
Grunnen til at vi nevner dette er at vi har gjort en måling av et annet solsystem enn det vi befinner oss i nå. Vi ser at stjerna til det solsystemet går i bane om et felles massesenter til en planet. Vi ønsker å beregne massen til den planeten.
Først må vi introdusere noe som kalles Dopplereffekten. Hvis du har stått langs veien, og en bil kjører fort forbi deg, vil du merke at lyden fra bilen endrer tone. Når den er langt unna er den dyp, og stiger jo nærmere den kommer. Når den har kjørt forbi deg blir den dyp igjen. Dette er Dopplereffekten. Når et objekt beveger seg mot en observatør, vil bølgene bli kortere. Dette gjelder alt av bølger. Både lyd og lys. Når et objekt beveger seg fra observatøren, blir bølgene lengre. Dopplereffekten er beskrevet ved
\(\frac{\Delta\lambda}{\lambda_0}=\frac{v_r}{c}\)
hvor \(\Delta\lambda\) er endringen i bølgelengde, \(\lambda_0\) er den faktiske bølgelengden, \(v_r\) er den radielle hastighetskomponenten og \(c\) er lysfarten \((3\cdot10^8m/s)\). Hvorfor ser vi på den radielle hastighetskomponenten? Jo, fordi det er denne komponenten som skaper en Dopplereffekt.
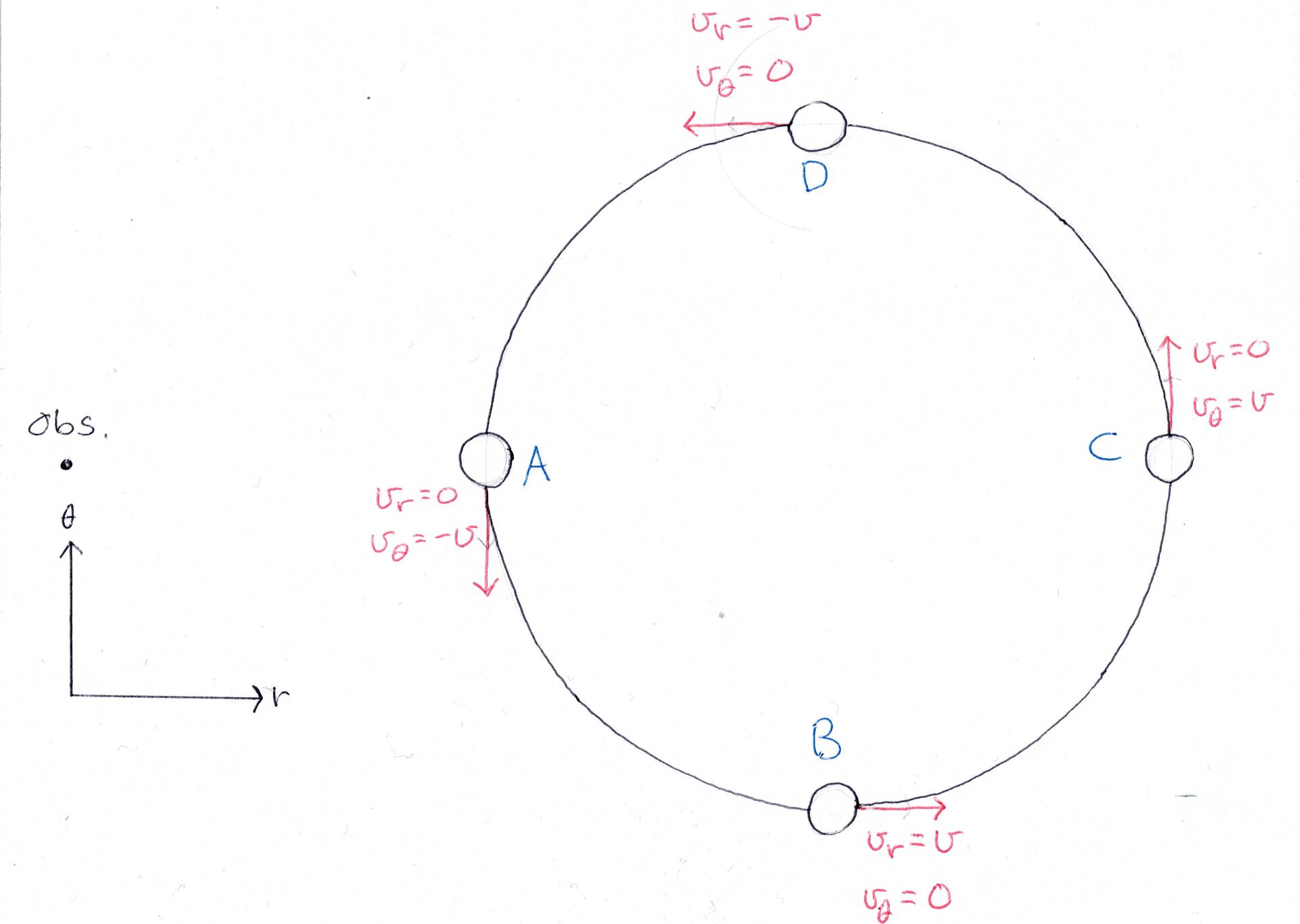
Når vi nå ser på banene er de ikke lenger ellipser, men tilnærmet sirkulære. Eksentrisiteten til banene er så små, at dette er greit å gjøre. I Figur 1 har stjerna en normal komponent \(v_{\theta}\) som beskriver hastigheten normalt på radiell retning, og en radiell komponent \(v_r\) som beskriver hastigheten radielt ut fra en observatør (obs.). Når stjerna er i punkt A og C, har den kun en hastighet i \(\theta\)-retning. Dette gir ingen Dopplereffekt, ettersom at stjerna verken beveger seg mot eller fra observatøren. Men i punkt B og D beveger stjerna seg radielt i forhold til observatøren. Det er her vi kan måle hastigheten. Merk også at avstanden fra observatøren til stjerna er veeeldig lang. Hvis dere på Jorda ser på den nærmeste stjerna utenom Sola, er det Proxima Centauri. Den ligger 4,2 lysår unna jorden. Se for dere å trekke en linje til det punktet som tilsvarer punkt B og punkt D i Figur 1. Den vinkelen mellom de to linjene er helt utrolig liten. Derfor kan vi tilnærme at de to linjene er parallelle. Den tilhørende hastighetskurven vil se noe slikt ut, for stjerna i Figur 1:

I punkt A har stjerna ingen radiell hastighet, og den målte hastigheten blir derfor 0. Deretter vil hastigheten stige mens stjerna beveger seg mot punkt B, hvor den vil få et toppunkt. Enig? Fint. Fra B vil hastigheten synke til den når punkt C, hvor den igjen blir 0. Herfra øker hastigheten i negativ retning til den når et bunnpunkt i D, hvor den øker mot 0 i A, igjen. Henger dere med enda? Ta gjerne litt ekstra tid hvis noe var uklart. Husk at vi kun kan måle den radielle hastigheten til stjerna, ettersom det er denne som vil gi en Dopplereffekt.
Nå er det enda en ting som kan påvirke målingene. Nemlig noe som kalles inklinasjonsvinkel. Hvis banen til stjerna har en vinkel i forhold til synsretningen til observatøren, vil det aldri være et punkt der den radielle hastighetskomponenten er den enste.
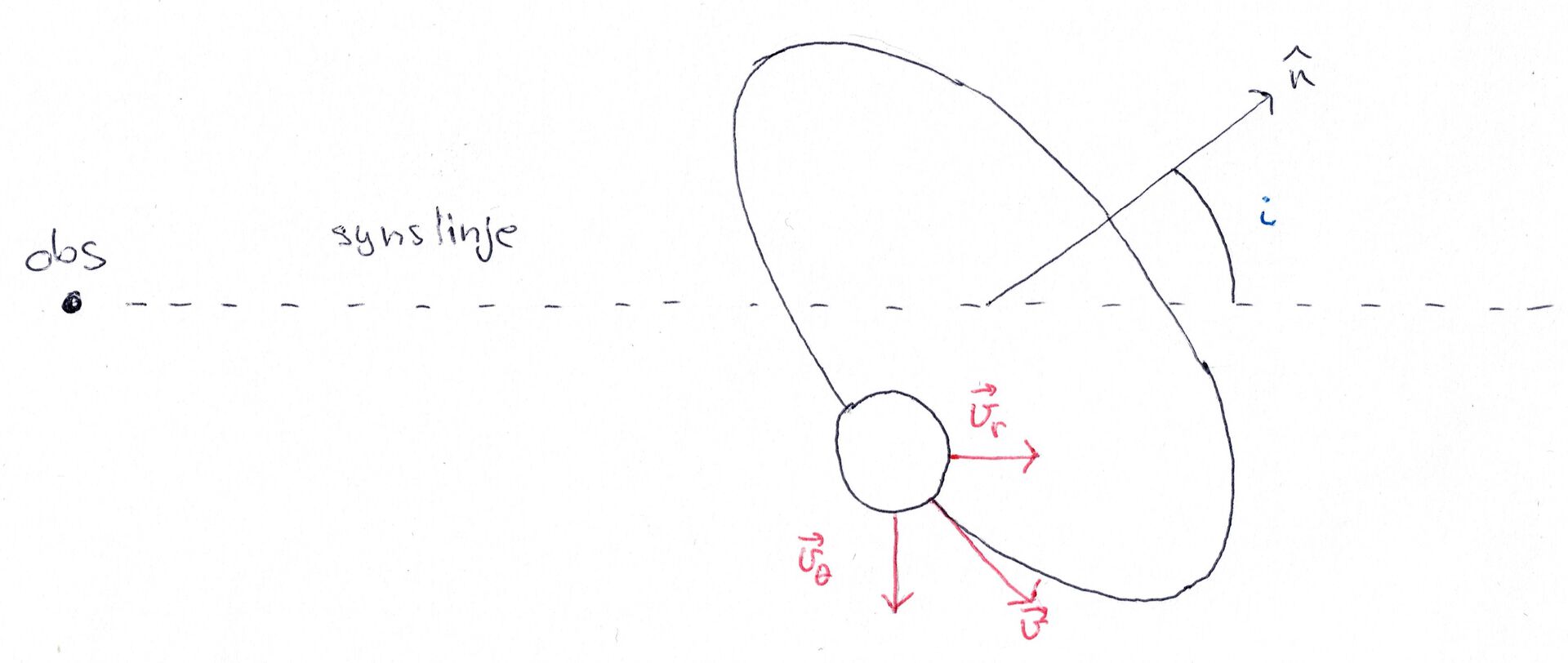
Dere ser at vi her aldri får isolert den radielle hastigheten. Men vi vil få en liknende kurve. Den vil se slik ut:
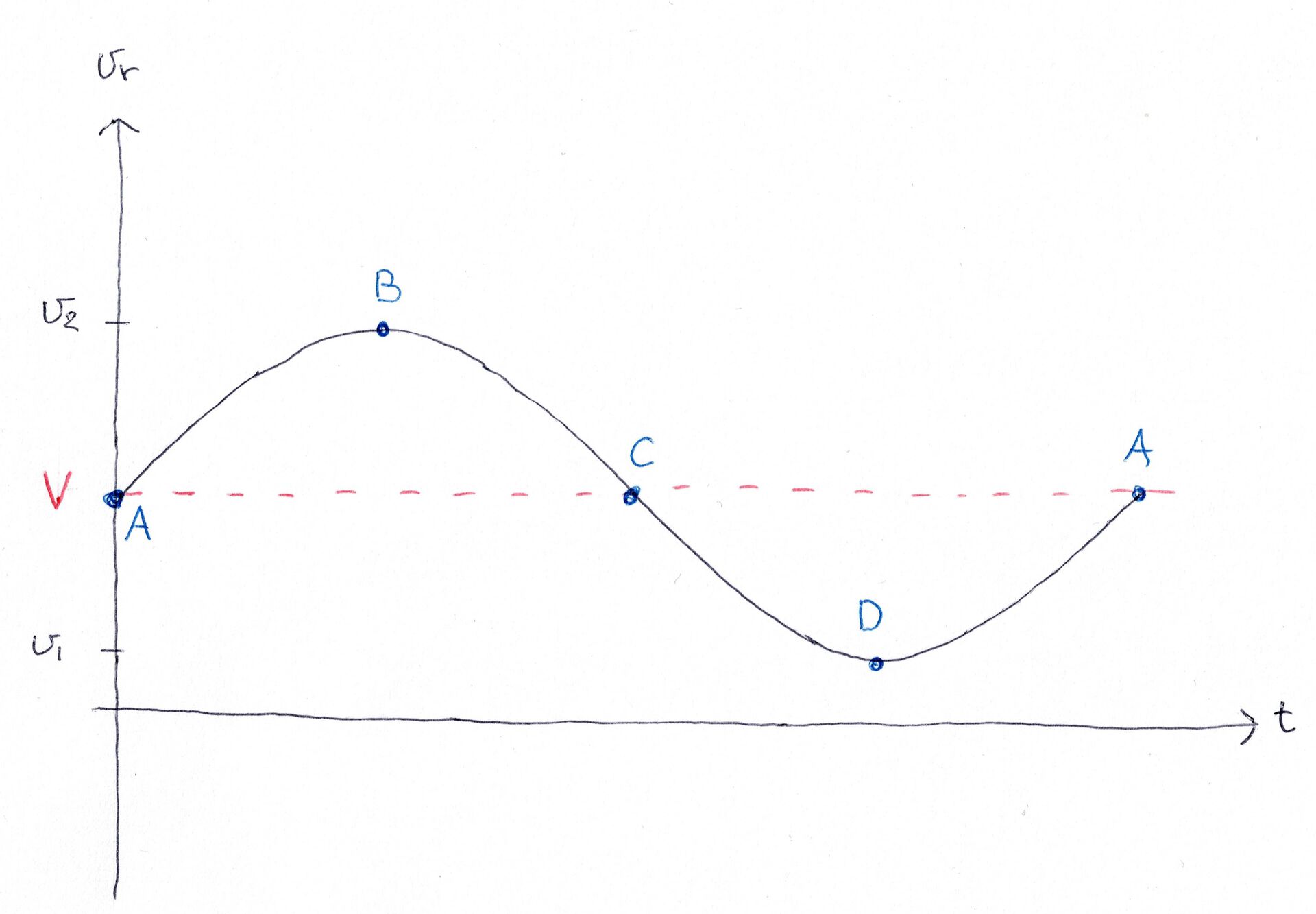
Ser dere her at når stjerna er i posisjon A og C, så vil den fortsatt ha en hastighet? Det er dette som er egenhastigheten, \(V\). Massesenteret vil bevege seg fra oss (det er også mulig at et system beveger seg mot oss, men da vil de tilsvarende punktene A og C gi negative verdier). Det gir oss at hastigheten til stjerna blir
\(v_*=v_{obs}-V\)
hvor \(v_{obs}\) er den observerte hastigheten, og \(V\) er egenhastigheten til systemet. Greit, nå skal vi gå litt videre. Det vi er ute etter her, er å si noe om massen til planeten som stjerna deler massesenter med. Dere kan lese mer her om to-legeme-problemet.
Nå definerer vi noen variabler. \(m_*\), \(v_*\) og \(a_*\) er henholdsvis massen, radien og absolutthastigheten til stjerna i sin bane rundt massesenteret. Tilsvarende har vi for planeten \(m_p\), \(v_p\) og \(a_p\). Vi har at
\(\begin{align*} v_*=\frac{2\pi a_*}{P}\quad\quad \quad v_p=\frac{2\pi a_p}{P} \end{align*}\)
Nå skal vi dra noe opp av hatten. Vi kan regne mye på dette og vise hvorfor det stemmer, men vi kommer ikke til å gjøre det. Formelen for å måle massen til en planet som går i bane om et felles massesenter til sin stjerne er
\(m_p=\left(\frac{P}{2\pi \gamma}\right)^{1/3}m_*^{2/3}\frac{v_{*,obs}}{sin(i)}\)
hvor \(i\) er inklinasjonsvinkelen til systemet, som beskrevet i Figur 3. Vi har også at den radiale hastighetskomponenten til stjerna er gitt ved funksjonen
\(v_{*,obs,r}(t)=v^B_{*,obs,r}cos\left(\frac{2\pi}{P}(t-t_0)\right)\)
hvor \(v^B_{*,obs,r}\) er den hastigheten stjerna har i det vi har kalt punkt B, altså den maksimale observerte hastigheten. Merk også at \(cos(\theta)\in[-1,1]\). Det vi ser er at \(t_0=t\) er det tidspunktet \(cos\) har et maksimum. Vi har tatt noen snarveier her og utelatt en del forklaring. Det grunner i at vi har litt dårlig tid. Beklager det.
Vi har fått disse målingene fra den andre stjerna sin hastighetskurve:
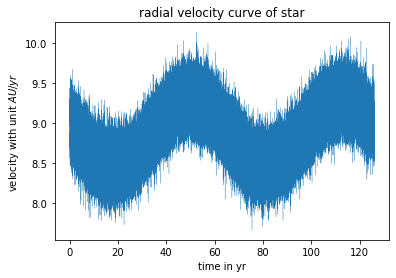
Huff og huff så rotete! Det første vi kan se er at når stjerna har maksfarten sin, så er den ikke null i Figur 5. Dette er da egenverdien til systemet. Vi leser av plottet og gir oss at denne må være omtrent \(8.875\,AU/yr\). Dette er så rotete på grunn av støy i vår måling. Flaks for oss at denne støyen er Gaussisk! Husk tilbake fra innlegget om statistikk at vi kan si noe om denne støyen. Vi vet at middelverdien ligger på 0. Den observerte hastigheten \(v_{obs}(t)\) er gitt ved
\(\begin{align*} v_{obs}(t)&=v_{faktisk}+\delta v(t)\\ \delta v(t)&=v_{obs}(t)-v_{faktisk} \end{align*}\)
hvor \(\delta v(t)\) er støyen vi måler, og \(v_{faktisk}\) er den faktiske hastigheten til stjerna. Dere har nok hatt mye om sannsynligheter, så da vet dere kanskje at sannsynligheter som er uavhengige av hverandre kan ganges sammen. For eksempel hvis dere skal kaste en terning, er sannsynligheten for at dere får 2 seksere på rad lik
\(\begin{align*} P(2\,seksere)&=P(sekser)\cdot P(sekser)\\ &=\frac{1}{6}\cdot\frac{1}{6}\\ &=\frac{1}{36}=2.7\,\% \end{align*}\)
Hvordan kan vi si noe om sannsynligheten for at vi måler riktig? Jo, ved å gange alle sannsynlighetene for at hastigheten har en eller annen støy, \(\delta v_i(t)\), sammen. Vi har at sannsynligheten for ett målepunkt er
\(P(\delta v_i)=\frac{1}{\sqrt{2\pi}\sigma_{støy}}e^{-\frac{1}{2}\left(\frac{v_{obs}(t)-v_{faktisk}(t)}{\sigma_{støy}}\right)^2}\)
Sannsynligheten for at vi vi måler en gitt støy for hvert punkt blir da
\(\begin{align*} P(\sigma v_1,...,\sigma v_n)=\frac{1}{\sqrt{2\pi}^n}\prod_{i=1}^n\frac{1}{\sigma_{støy}}e^{-\frac{1}{2}\sum_{i=1}^n\left(\frac{v_{obs}(t)-v_{faktisk}(t)}{\sigma_{støy}}\right)^2} \end{align*}\)
Hva sier dette oss? Jo, det sier oss at det som står i eksponenten til \(e\) må bli minst mulig for at sannsynligheten skal bli størst. Dette kalles minste kvadraters metode. Vi har at \(\sigma_{støy}\) er konstant, så vi kan omformulere hele problemet til
\(\begin{align*} \Delta=\sum_{t_i}\bigg(v_{obs}(t_i)-v_{faktisk}(t_i)\bigg)^2 \end{align*}\)
Hvis vi får \(\Delta\) minst mulig, vil sannsynligheten for at vi har valgt riktig være størst. Vi har valgt følgende verdier, hvor egenhastigheten har blitt trukket fra \(v_*\)
| \(v_*\) | \(P\) | \(t_0\) |
| \([-0.125,0.875]\) | \([40,80]\) | \([40,60]\) |
Hvis dere ser på Figur 5 ser dere at de intervallene vi har valgt må inneholde de faktiske verdiene. Vi deler opp alle intervallene i 20 og bruker minste kvadraters metode på alle mulige kombinasjoner av dem. Dessverre for oss gir det oss dette plottet:
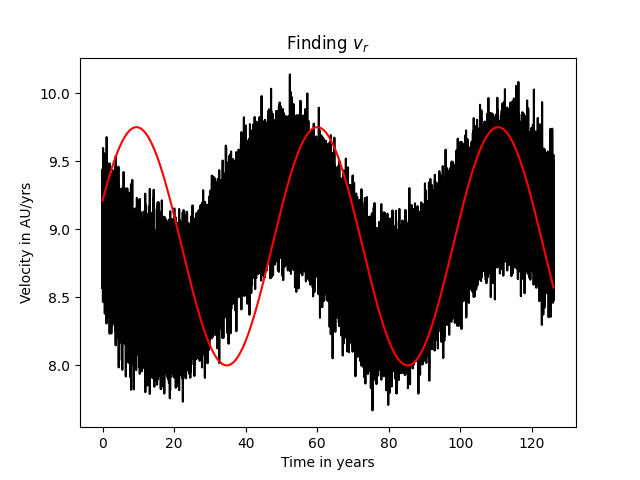
Vi har åpenbart gjort en feil. Dette kan skyldes feil i hvordan vi har regnet ut modellen vår, eller hvordan vi har implementert dette i koden. Det vi ser er at utslagene er litt høye, og at fasen er forskjøvet. De tallene vi fikk var
\(v_*=0.875, \quad\quad P=50.5,\quad\quad t_0=60.0\)
Dette stemmer åpenbart ikke, ettersom at både for \(v_*\) og \(t_0\) har vi fått de høyeste verdiene kurven kunne ha. Ved direkte avlesning kan vi gjette på disse verdiene:
\(v_*=0.375, \quad\quad P=65,\quad\quad t_0=50\)
Det gir oss dette plottet:
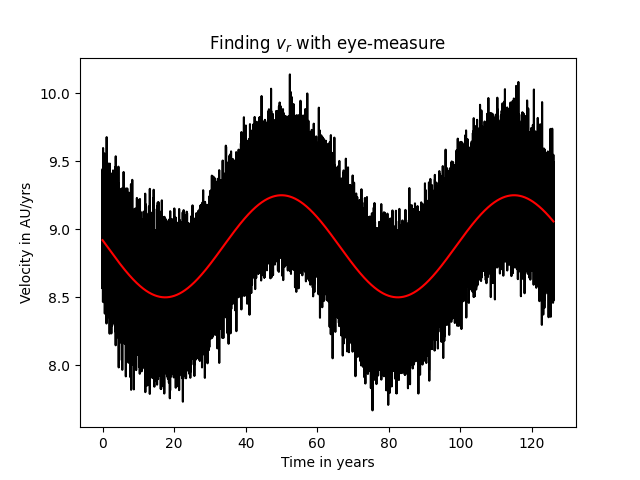
Denne passer mye bedre, men som sagt, dette er ikke de verdiene med størst sannsynlighet, bare de vi har sett med det blotte øye.
Nå er det på tide å prøve å beregne den minste massen planeten kan ha. Husk at
\(m_p=\left(\frac{P}{2\pi \gamma}\right)^{1/3}m_*^{2/3}\frac{v_{*,obs}}{sin(i)}\)
Hvis vi velger inklinasjonsvinkelen til å være \(i=90^\circ\) vil dette gi den minste mulige massen til planeten. Noen mindre vinkel vil øke massen med en faktor \(1/sin(i)\).
Vi vet massen til stjerna, som er svimlende \(3.99\,M_{\odot}\). Denne stjerna vil bli et sort hull når den dør. Grensen ligger på mellom 2 og 3 solmasser. Vi putter dette inn i formelen vår, som gir
\(\begin{align*} m_p&=\left(\frac{65}{2\pi\cdot4\pi^2}\right)^{1/3}3.99^{2/3}\cdot0.375\\ &\approx0.604\,M_\odot \end{align*}\)
Nok en fiasko. Den riktige størrelsen skal være \(0.0384\,M_\odot\). Nå er jeg veldig usikker på hvor det har gått galt, men det er viktig å tenke på at tallene vi har brukt er svært unøyaktige. Hvis dere ser på formelen, så ser dere at det som skal til for å få et mindre svar er at omløpstiden og maksimal radiell hastighet er mindre. Dette kan det godt være våre øyne har feilet med.
Det var alt vi hadde å fortelle dere nå. Det er synd vi ikke fikk til dette, men vi håper dere som leser kan ha fått noe utbytte likevel. Til neste gang, farvel.
