Gass virker som en tilfeldig ting i hverdagen, noe man har lite kontroll på hvordan vil oppføre seg. Det er kanskje sant, men ikke helt sant. Vi skal nå prøve å modellere hydrogengass (\(H_2\)) inne i en bitteliten boks som til slutt skal virke som vår rakettmotor i denne modellen, og for å gjøre dette er det et par ting vi først bør ta stilling til.
I vårt tilfelle vil vi anta at vi har noe som kalles ideell gass. Dette er kanskje et ukjent konsept for noen, men la meg prøve å oppklare hva slags antakelser som skiller en ideell gass fra en virkelig gass:
- Gasspartiklene er like store, samme form, og antas å være punktpartikler.
- Gasspartiklene utveksler ingen intermolekylære krefter, dvs. de ikke tiltrekker eller frastøter hverandre. I vår modell vil de heller ikke kollidere med hverandre, men kun veggene på boksen.
- Volumet på partiklene er neglisjert, og hastighetene på gassen er tilfeldig.
- Kollisjonene til partiklene med veggene i boksen er 100% elastiske. Sagt på en annen måte, er bevegelsesmengden bevart for hver partikkel. Husker du ikke heeeeeelt hvordan bevaring av bevegelsesmengde var? Da kan du friske opp minnet ditt her!
MERK! Jeg skriver tilfeldig, men tilfeldig er kanskje ikke så tilfeldig som du tror. La oss se litt på statistikken bak hastigheten til disse partiklene før vi ser på hvordan vi skal simulere denne lille boksen på datamaskinen som til slutt skal bli en rakettmotor!
Statistikk - ja, det er faktisk viktig
Når vi skal dele ut hastighetene til alle partiklene i en ideell gass, så er det viktig å vite at hver hastighetskomponent følger noe som kalles en normal distribusjon eller også Gaussisk distribusjon. Distribusjonen forteller deg noe om hvordan farten er fordelt i en gass, eller hvor sannsynlig det er at en gasspartikkel har en eller annen fart. Jeg skal nå kaste et litt hårete uttrykk på deg, så ikke bli skremt av at det ser komplisert eller skummelt ut. Du behøver ikke å forstå hvorfor formelen ser sånn ut, og jeg skal prøve å ta deg gjennom de ulike tegnene som er i den. Formelen for distribusjonen av hver enkelt komponent ser sånn ut:
\(P(v_x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(\frac{v_x - \mu}{\sigma}\right)^2}\)
MERK at jeg her skriver \(v_x \), men at samme fordeling gjelder for de andre komponentene \(v_y\) og \(v_z\), altså er alt jeg skriver om \(v_x \) og \(P(v_x)\) analogt med \(v_y\) og \(P(v_y)\) og \(v_z\) og \(P(v_z)\). Så hva er det egentlig som skjer her? Hva er \(\mu\) og \(\sigma\), og hva er \(P(v_x)\)? La oss plotte funksjonen så vi kan se hvordan den ser ut først. Funksjonen er plottet for hydrogengass (\(H_2\)).
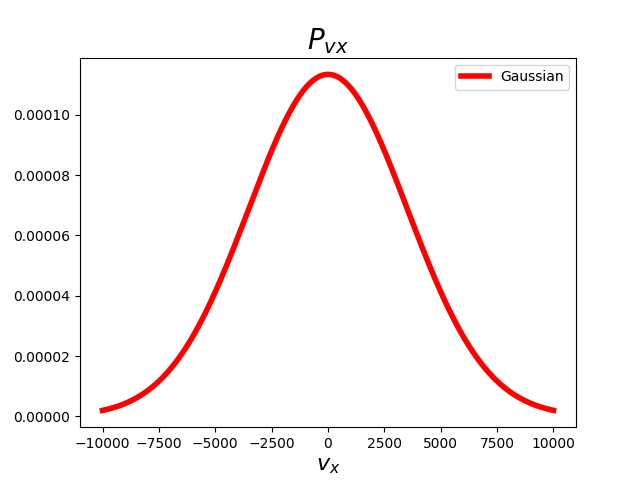
Det første vi kan legge merke til her er at funksjonen er symmetrisk om \(v_x=0\). Hva forteller dette oss? Jo, det er like sannsynlig at en partikkel har negativ \(v_x\)-komponent som positiv \(v_x\)-komponent. Altså er det like sannsynlig at partikkel vil gå av sted i alle retninger (husk at fordelingen også gjelder \(v_y\) og \(v_z\)). Det betyr også at middelverdien av \(v_x\), ofte notert som \(\langle v_x\rangle\), må bli \(0\)! Middelverdien er jo bare summen av alle verdiene delt på antall verdier, men siden distribusjonen er symmetrisk om \(v_x = 0\) så vil det for hver \(v_x\) finnes en helt lik \(v_x\) med motsatt fortegn, og da blir summen av disse \(0\). Det er hva \(\mu \) er! \(\mu \) er middelverdien i en fordeling, og i tilfellet for ideell gass så er \(\mu = \langle v_x \rangle= \langle v_y \rangle = \langle v_z \rangle= 0\). Det vi også ser på grafen er at der \(v_x=0\) har også \(P(v_x)\) et toppunkt. Hva \(P(v_x)\) egentlig er har jeg enda ikke sagt så mye om enda, og det kommer jeg til snart. Først vil jeg fortelle litt om hva \(\sigma \) betyr.
\(\sigma \) er det vi kaller standardavviket, som er et gjennomsnittlig mål på hvor mye noe avviker fra middelverdien. La oss for eksempel si at gjennomsnittshøyden i Norge er 180cm. Dersom vi lar standardavviket være 5cm, betyr det at om vi trekker ut en tilfeldig person så er det sannsynlig at de har en høyde som ligger mellom 180-5cm og 180+5cm, eller \(\mu - \sigma\) og \(\mu + \sigma \). Standardavviket fungerer også som et mål på hvor bred denne Gaussiske kurven er, jo bredere standardavviket er, jo bredere må kurven bli, siden avviket er større fra middelverdien. Dette har en konsekvens for middelverdien, siden den må bli lavere. Dette er fordi integralet under kurven alltid må være 1, som betyr at når kurven blir bredere må den også bli lavere. Hvorfor integralet over kurven alltid må være 1 kommer vil du forhåpentligvis forstå bedre i neste avsnitt. For en ideell gass vet vi at \(\sigma = \sqrt{\frac{kT}{m}}\), der \(k\) er Boltzmanns konstant (Boltzmanns konstant kan du lese om her), \(T\) er temperaturen i gassen gitt i Kelvin, og \(m\) er gasspartikkelens masse.
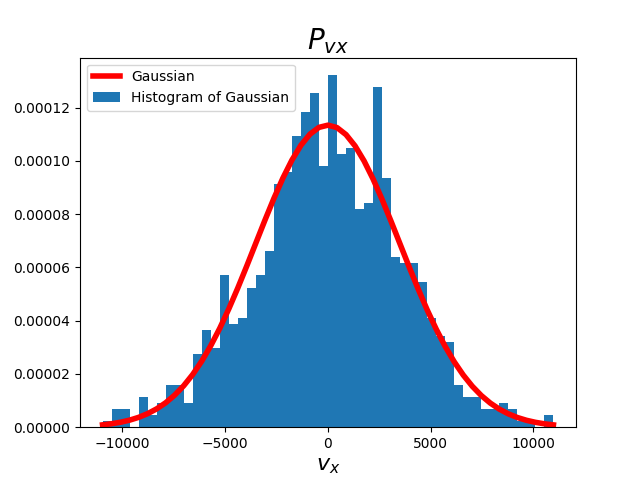
\(P(v_x)\) er sannsynlighetstettheten for \(v_x\)-komponenten i en hastighet \(\vec{v} = (v_x, v_y, v_z)\), altså en sannsynlighet pr. fart. Dette er kanskje en litt uvant og abstrakt størrelse, men gir mening dersom vi integrerer over den mellom et intervall (husk at et integral egentlig bare er et produkt av aksene). Det vil si at om vi integrerer \(P(v_x)\) med hensyn på \(v_x\) i et eller annet intervall, la oss si mellom \(100m/s\) og \(200m/s\), vil vi få sannsynligheten for at en gasspartikkel har en \(v_x\) mellom \(100m/s-200m/s\). Det betyr det at om vi integrerer over \(P(v_x)\) med hensyn på \(v_x\) fra \(-\infty\) til \(\infty\) vil vi få 1, siden sannsynligheten for at en partikkel har en hvilken som helst fart er mellom \(-\infty\) og \(\infty\) er 1, eller 100%. Det betyr også at sannsynligheten for at en partikkel har en nøyaktig bestemt fart også er \(0\), siden vi da integrerer fra f.eks \(100m/s\) til \(100m/s\), som vil gi oss 0. Dette gir forhåpentligvis mening siden alle tall er uendelige desimaler, og sannsynligheten for at en fart skal ha alle de uendelige desimalene, at absolutt alle desimalene skal matche må være 0. Derfor er det normalt å plotte dataene i noe som kalles histogrammer, som plotter fordelingen i såkalte bins, som bare er et intervall. Altså samler vi sannsynligheten for at en partikkel ligger i et intervall og plotter disse. Jeg går ikke noe særlige dypere inn på det, men legger til et bilde av hvordan noe sånt kan se ut for helt tilfeldige genererte data med en kommando fra Numpy-modulen i Python kalt np.random.normal(). med Gaussisk/normal fordeling for en hydrogengass:
Nå er det nok om statistikk! Det kan fort bli litt *snork* med mye statistikk, men det er veldig viktig for å simulere gassen riktig. La oss begynne å se på boksen og rakettmotoren!