Hvor skal vi starte?
Det første vi kan begynne med er ideen bak boksen. Hvordan skal den funke? Hvordan kan vi simulere dette? Vil det funke? Dette er alle spørsmål vi skal få svart på nedenfor, og vi kommer til å bruke Python for å gjennomføre det.
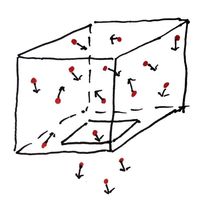
Ideen bak hvordan boksen skal funke er at det er masse partikler i boksen som fyker rundt, og som gir fra seg bevegelsesmengde til raketten. Så lenge partikkelen er i boksen og kolliderer med veggene, vil bevegelsesmengden pr. vegg hoppe litt frem og tilbake, men være omtrentlig 0 fordi bevegelsesmengden på den ene veggen "kanselleres" når partikkelen kolliderer med veggen på andre siden. MEN med en gang en partikkel unnslipper ut gjennom hullet på bunnen av boksen, vil ikke bevegelsesmengden fra partikkelen på taket bli "kansellert" av kollisjonen partikkelen har med gulvet i bunnen, og raketten "beholder" bevegelsesmengden partikkelen overførte til taket av boksen. For de av dere som har fysikken på plass, så husker dere at \(\vec{F} = \frac{\Delta \vec{p}}{\Delta t}\) der \(\Delta\vec{p}\) er endringen i bevegelsesmengde og \(\Delta t\) er endring i tid, og dermed vil det virke en kraft på boksen. Denne kraften trenger vi for å vite hvor mye kraft raketten får fra motoren til slutt, og når vi begynner å telle antall partikler som forlater boksen kan vi regne ut massen som forsvinner ved å gange opp antall partikler ut med massen til partiklene.
Så hvordan lager vi denne boksen? Vi starter med å definere alle de nødvendige parameterne som temperatur, antall partikler og størrelse på boksen. Det er viktig å få med at antallet partikler i boksen vil være det samme hele tiden, dvs. at når en partikkel forsvinner ut, vil en ny partikkel komme inn igjen. Videre vil vi bruke numerisk integrasjon for å finne hastighet og posisjon til hver partikkel i boksen. Metoden for numerisk integrasjon vi vil bruke her kalles Eulers metode for numerisk integrasjon. Det er ikke den beste eller mest avanserte metoden for integrasjon, men vil være godt nok for et kort tidsintervall (i senere bloggposter kommer vi til å bruke mer nøyaktige og avanserte metoder for numerisk integrasjon). På denne måten vet finner vi hastigheten og posisjonen til partiklene. Mens partiklene virrer rundt må vi også teste for kollisjoner mellom partikkel og vegg, og snu fortegnet på en av komponentene i hastigheten så partikkelen ikke flyr vekk gjennom veggene. Vi blir også nødt til å registrere når en partikkel forsvinner ut av hullet og antallet partikler som forsvinner ut, slik at vi kan regne ut hvor mye masse vi taper og kraften vi får i boksen. Nå tar vi hvordan-delen i litt dypere detalj:
Vi setter noen faste parametere nå, som vi kan tweake på senere. I første omgang bruker vi:
\(\text{sidelengde på vegg}=10^{-6}m,\:T=3000K,\:\text{antall partikler} = 10^5,\:\text{sidelengde på hull}=0m\)
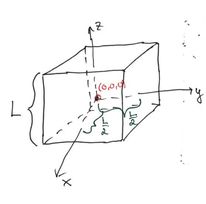
Som du ser starter vi uten noe hull i bunnen av boksen. Den legger vi til litt senere. Det er også viktig å presisere hvordan vi har definert koordinatsystemet i boksen. Boksen er definert slik at origo (punktet (0,0,0)) ligger midt i boksen. Det betyr at dersom sidelengden til boksen er \(L=10^{-6}m\), vil f.eks veggen langs x-aksen i boksen ligge på koordinatene \(\left(\frac{L}{2},0,0\right)\) og \(\left(-\frac{L}{2},0,0\right)\), og analogt med y og z-aksen.
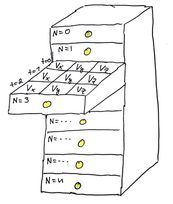
Det neste steget er å lage to arrays fylt med null: en som skal inneholde posisjonene til alle partiklene ved et tidspunkt, og en som skal inneholde alle hastighetskomponentene til partiklene. En array er en slags datastruktur, som en kommode med skuffer og inndelinger oppi skuffene så vi kan samle dataene våre der, litt som i figur 6. Eneste forskjellen er at vi kun vil ha det for ett tidspunkt om gangen, altså vil vi ha 100 000 antall skuffer for partikler, 1 inndeling for tid, og 3 inndelinger for hver komponent. Dette er fordi om vi skulle lagret dataen for alle posisjonene og hastighetene til 100000 partiklene for alle de små tidsstegene (vi kommer til å bruke et lite tidssteg \(dt = 10^{-12}\) og gå gjennom 1000 steg med integrasjon) vi tar, ville vi endt opp med 600 000 000 elementer som skulle lagres! Da vil du rett og slett ende opp med et minneproblem på pc'en din som gjør at du ikke får kjørt koden at all.
Euler - en ganske allsidig mann
Nå som vi har disse arrayene fulle av null, ønsker vi å sette en initialposisjon og initialhastighet for hver enkelt partikkel. Hvorfor vil du forhåpentligvis forstå senere, om du allerede ikke vet det. Det finnes mange gode metoder for å gjøre dette, men vi valgte en enkel og kanskje litt treg måte å gjøre det på: nemlig gå gjennom arrayene og sette dem for hver partikkel én etter én. Men hva skal starthastighetene og startposisjonene være? Nå får vi bruk for statistikken fra tidligere! Vi vet nemlig at en ideell gass har gaussisk distribusjon på hastighetskomponentene. Vi gir hver enkel partikkel et tilfeldig tall fra gaussisk distribusjon, og vi brukte en random-funksjon i Python som gjør dette for oss, kalt random.gaussian(mu, sigma), som gir oss et tilfeldig tall fra gaussisk distribusjon. Da sender vi inn \(\mu = 0\) og \(\sigma = \sqrt{\frac{kT}{m}}\) som gjelder for ideell gass. Hva med posisjon? Vel, partiklene har ingen god grunn til å befinne seg på et sted i rommet fremfor et annet sted. Derfor fordeler vi partiklene uniformt i rommet, som vil si at det er like sannsynlig å finne en partikkel et sted i boksen som et annet sted i boksen. Vi bruker samme metode som for hastigheten, og bruker en random.uniform(-L/2, L/2) til å fordele posisjonene. Da har vi alt vi trenger for å integrere numerisk med Eulers metode.
Eulers metode er en form for numerisk integrasjon. Det man gjør er å regne ut hastighet og posisjon et biiiiiittelite tidssteg \(dt\) etter den forrige hastigheten og posisjonen, gitt at man har et uttrykk for akselerasjonen. Det finnes mange måter å vise hvor Eulers metode kommer fra, men jeg liker ofte å vise det med definisjonen av den deriverte:
\(\begin{align*} a(t) &= \frac{v(t+dt) - v(t)}{dt} \\ \Rightarrow v(t + dt) &= v(t) + a(t)\cdot dt \\ \\ v(t) &= \frac{r(t+dt) - r(t)}{dt} \\ \Rightarrow r(t+dt) &= r(t) + v(t)\cdot dt \end{align*}\)
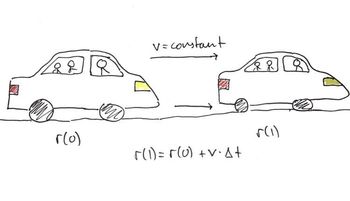
Her faller uttrykkene rett ut fra definisjonene! Farten i et lite tidssteg dt etter tiden t er farten i tidspunktet t pluss akselerasjonen i tidspunktet t ganget med det lille tidssteget, og samme med posisjonen. Dette er Eulers metode! Husk at \(dt\) er en infinitesimal størrelse, altså en uendelig liten størrelse, så våre tall på datamaskinen blir kun en approksimasjon, og vi må bruke små tidssteg \(\Delta t \). I vårt tilfelle akselererer ikke partiklene, altså er \(a(t) = 0\), så farten slipper vi å regne ut (husk at bevegelsesmengden er bevart, så farten til partiklene er de samme hele veien, men bytter fortegn på en komponent ved kollisjon med vegg. Glemt det allerede? Sjekk det ut her!). Uttrykket vi sitter igjen med å datamaskinen er da kun \(r(t + \Delta t) = r(t) + v(t)\cdot\Delta t\) som vi trenger å regne ut. Det vi gjør da er å bruke en loop til regne ut tidssteg for tidssteg. Vi bruker et biiitelite intervall \(\Delta t = 10^{-12}\), og regner ut 1000 steg av loopen. Da vil den totale tiden for simulasjonen av boksen være \(t_{total} = 10^{-9}\). Sekvensen vil se noe sånn ut:
\(\begin{align*} r(10^{-12}) &= r(0) + v(0)\cdot10^{-12} \\ r(2\cdot10^{-12}) &= r(10^{-12}) + v(10^{-12})\cdot10^{-12} \\ r(3\cdot10^{-12}) &= r(2\cdot10^{-12}) + v(2\cdot10^{-12})\cdot10^{-12} \\ &... \\ &... \\ r(999\cdot10^{-12}) &= r(998\cdot10^{-12}) + v(998\cdot10^{-12})\cdot10^{-12} \\ r(1000\cdot10^{-12}) &= r(999\cdot10^{-12}) + v(999\cdot10^{-12})\cdot10^{-12} \\ \end{align*}\)
Også er den ferdig etter 1000 steg. Ser du nå hvorfor vi trengte en initialhastighet og initialposisjon ved t=0? Vi bruker vektorisering for å regne ut posisjonen til alle partiklene samtidig, så det skal gå litt fortere.

Mellom hver eneste gang vi regner ut en ny posisjon for partiklene, looper vi gjennom alle partiklene for å sjekke posisjonene deres og evt. bytte fortegnet på en komponent dersom de har kollidert med en vegg. Vi kunne også brukt vektorisering for å sjekke veggkollisjoner, som ville vært kjappere og mer elegant, men å gå gjennom alle partiklene en etter en funker det også. Måten vi tester det på er å teste om hvert enkelt koordinat for hver partikkel er større eller mindre enn \(\frac{L}{2}\) eller \(-\frac{L}{2}\). På den måten har vi kontroll på om koordinatene til partikkelen er i boksen eller ikke. Da må vi passe ekstra godt på om \(\Delta t \)-en vår er liten nok, ellers vil partikkelen fly ut av veggen på boksen mellom et tidssteg uten at vi fanger det opp. Vi kjører simuleringen for \(N=3\:\text{antall partikler}\) og plotter banene til partiklene, bare for å se om det ser riktig ut:
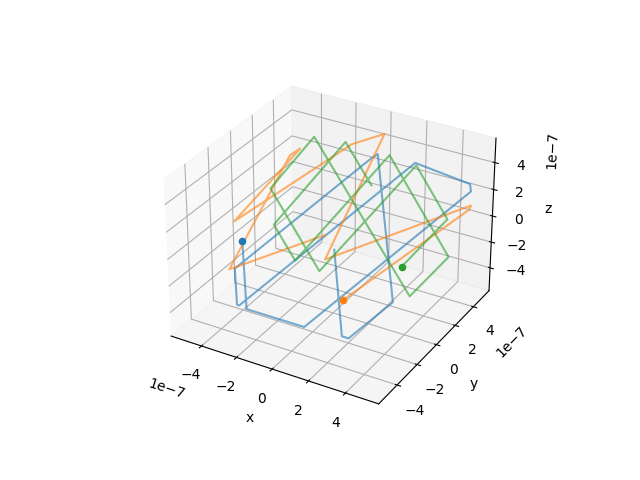
Dette ser veldig lovende ut! Partiklene spretter fint inne i boksen uten å forsvinne ut. En annen måte å sjekke om det stemmer på er å regne ut det analytiske trykket i boksen og det numeriske trykket i boksen, og sammenlikne. Det analytiske uttrykket for trykk av gass i et volum er \(P = \frac{N}{V}kT\) , der \(N\) er antall partikler, \(V \) er volumet gassen befinner seg i, \(k\) er som tidligere Boltzmanns konstant og \(T\) er temperatur i kelvin. Vi kjører en simulering av boksen der vi regner ut det numeriske trykket. Vi husker at trykk også er gitt som \(P = \frac{F}{A}\), men vi mangler et uttrykk for kraften. Heldigvis utledet Johan dette i en tidligere post om bevegelsesmengde som du kan lese her. Det tar vi for gitt, og vi vet nå at kraften fra en enkel partikkel er \(F = \frac{2p_z}{\Delta t}\), der \(p_z\) er bevegelsesmengde for partikkelen i z-retning, og \(\Delta t\) er tiden for hele simuleringen (\(10^{-9}s\)). Dette gir oss uttrykket \(P = \frac{2p_z}{\Delta tA}\), der alle nevnte størrelser er som for, og \(A\) er arealet på flaten kraften virker på. Vi summerer dette sammen for hver gang vi registrerer at en partikkel traff en eller annen vegg, og deler det på antall sider i boksen for å få et fint gjennomsnitt av trykk pr. vegg. Det numeriske trykket blir da \(P=4111.093Pa\). Vi kaster de samme tallene inn i formelen for det analytiske trykket, og får \(P=4141.947Pa\). Litt avvik må vi forvente fra datamaskinen og dataen vi har, og tallene er veldig like. Dermed kaller jeg det suksess! Vi kan nå introdusere hullet i bunnen av esken.
Når vi introduserer hullet i esken er det tre nye ting å ta hensyn til: størrelsen på sidelengden av hullet, testing av når en partikkel går ut av hullet, og hva som skjer med en partikkel når den forlater hullet (HUSK! Antallet partikler i boksen skal være det samme under hele simuleringen). Vi legger inn at sidelengden på hullet er halve lengden av boksen, dvs. \(\text{sidelengde hull} = 0.5\cdot10^{-6}\), slik at arealet av hullet er en fjerdedel av arealet på bunnen. Når vi skal registrere om en partikkel går ut av hullet, bruker vi samme praksis som da vi testet for veggkollisjon. Under testen der vi sjekket om partikkelen treffer gulvet legger vi en ny test, som tester om x og y-koordinatet til partikkelen er mindre enn sidelengden til hullet. Hvis x og y-koordinatet til partikkelen er mindre enn sidelengden til hullet, registrerer vi at en partikkel gikk ut og legger til +1 på antall partikler som har gått ut. Denne starter selvfølgelig på 0. I tillegg regner vi ut bevegelsesmengden \(p_z\) som overføres til taket av boksen. Denne kan vi bruke til å regne ut total kraft fra boksen senere, ved å bruke at \(F = \frac{2p_z}{\Delta t}\), der \(\Delta t \) er tiden for hele simulasjonen. Siden \(\frac{2}{\Delta t}\) er felles for kraften fra alle partiklene trenger vi kun å summere opp bevegelsesmengden, og kaste den inn i uttrykket senere. Vi regner ut \(p_z\) ved å summere opp bevegelsesmengden i z-retning til en partikkel hver gang den forlater hullet, selv om bevegelsesmengden teknisk sett overføres når partikkelen treffer taket. Men på denne måten slipper vi å legge til og trekke fra bevegelsesmengde hver gang en partikkel kolliderer. Totalt massetap regner vi også etter at loopingen er ferdig, siden\(\text{totalt massetap} = \text{antall partikler}\cdot \text{massen til partiklene}\). Men siden det kun er for \(10^{-9}s\), må vi gange det opp med \(10^9\) (eller dele det på den totale tiden for simuleringen) for å få totalt massetap pr. sekund. Da er \(\text{totalt massetap pr. sekund} = \frac{\text{antall partikler}\cdot\text{massen til partiklene}}{\text{total tid}}\). Men hva skjer nå med partikkelen som forlot boksen? Vi gjør det veldig enkelt, og bare kaster den tilbake i posisjonen \(\left(0,0,\frac{L}{2} - 10^{-12}\right)\) som om ingenting har skjedd. Vi trekker fra en bitteliten del av posisjonen slik at koden ikke skal registrere det som en veggkollisjon og snu fortegnet på z-komponenten av hastigheten til partikkelen. Vi velger derimot å beholde hastigheten til partikkelen som forsvant ut, for å bevare bevegelsesmengden og den gaussiske distribusjonen. Hadde vi valgt å gi den "nye" partikkelen som kommer inn en nye gaussiske hastighetskomponenter kunne det hende at vi forskyver den gamle distribusjonen, og ødelegger den gamle distribusjonen.
Resultater fra boksen
Vi kjører en simulering av boksen med parametere:
\(L=10^{-6}m,\:T=3000K,\:N=10^5,\:l=0.5\cdot10^{-6}m\) , der \(L\) er sidelengden på boksen, \(T\) er temperaturen i boksen gitt i kelvin, \(N\) er antall partikler i boksen, og \(l\) er sidelengden på hullet på bunnen av boksen. Tallene for kraft og massetap pr. sekund pr.boks blir da:
| N (antall partikler) | \(45934999999999 \) |
| thrust (N : Newton) | \(7.329079237148241\cdot10^{-10}N\) |
| Bevegelsesmengde (kgm/s) | \(7.329079237148241\cdot10^{-10}kgm/s\) |
| massetap pr. sekund (kg/s) | \(1.5374972752499938\cdot10^{-13}\frac{kg}{s}\) |
Det som kanskje er verdt å kommentere på først her er at total bevegelsesmengde fra boksen ila. et sekund er det samme som thrust-force for raketten. Det høres kanskje veldig rart ut, men dersom vi har total mengde bevegelsesmengde ila. simuleringstiden på \(10^{-9}s\) så vil det være ca. \(p = 7.33\cdot10^{-19}kgm/s\). Dersom vi deler dette igjen på \(10^{-9}s\) vil vi få total bevegelsesmengde pr. sekund, og vi ser på dimensjonene også at det går fra \(\frac{kgm}{s}\) til \(\frac{kgm}{s^2}\), som er enheten for kraft. Vi vet at arealet på undersiden av raketten vår er \(16m^2\), så dersom én liten boks har sidelengde \(10^{-6}m\) har boksen en underside med areal \(10^{-12}m^2\). Det betyr også da at \(10^{12}\) antall bokser vil ta opp \(1m^2\). Dermed kan vi tillate oss å bruke så mye som \(1.6\cdot10^{13}\) antall bokser uten at det tar for mye plass. Bruker vi så mange bokser for å lage en rakket vil vi ende opp med en motor som har drivkraft på ca. \(11.72\cdot10^{3}N\) og massetap \(2.46\frac{kg}{s}\).
Dette er tall med parametere vi kommer til å endre senere. For eksempel kan det hende vi gjør boksen mindre slik at vi får høyere antall-tetthet av partikler, som gir oss mer trykk i boksen og derav mer kraft. Med justering av boks-størrelse kommer også naturligvis en justering av utslippshullet. Vi kommer til å justere antall partikler, og antakeligvis putte litt flere partikler inn i boksen. Parametere vi skal prøve å holde urørt temperatur, mest fordi forbrenningstemperatur på hydrogengass faktisk er \(3000K\). Høyere temperatur vil også gi oss mer kraft, men vi prøver å holde den der den er. Vi kommer også til å beholde et antall bokser slik at rakettmotoren vil ta opp alle de \(16m^2\) vi har til gode på undersiden av raketten vår, dermed justeres antallet ut ifra størrelsen på boksen.
Skal vi til verdensrommet?
For å få kål på dette må du til neste innlegg.