Hjelpes meg, for en spennende dag dette er! Vi har bygd en rakett! Den er testet og godkjent (av oss), og nå skal vi se om ikke teorien vår fungerer. Vi har dette scenarioet, hvor \(\vec{R}\) er vektoren som peker på posisjonen til raketten fra systemets sol, \(\vec{F}\)er gravitasjonskrafta fra planeten på raketten, \(\vec{T}\) er rakettens thrust, \(\vec{v}\) er hastigheten til raketten og \(\vec{v_0}\) er initialhastigheten raketten får ved oppskytning på grunn av rotasjonshastigheten \(\omega\).
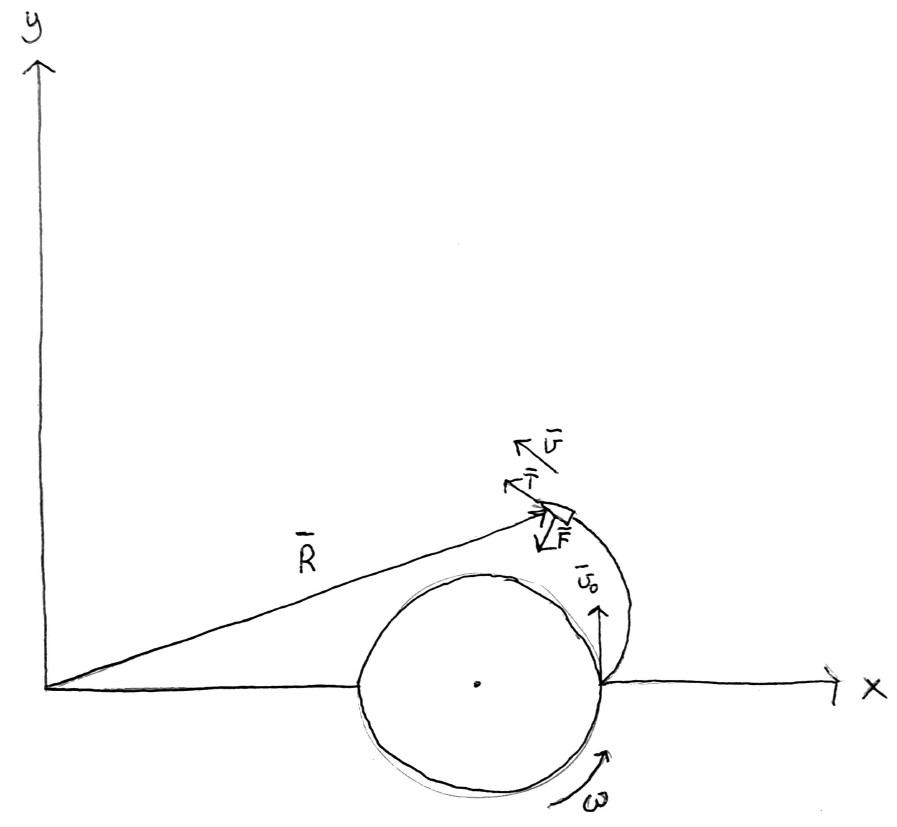
1. Vi har en rakett som står på planeten sin overflate, som vist på Figur 1.
2. Vi vil ha en initialhastighet i y-retning som kommer fra planetens rotasjon om sin egen akse.
3. Planetens tyngdefelt vil trekke oss mot planeten, mens rakettens thrust (skyvkraft) vil prøve å overvinne dette.
4. Vi anser å være i verdensrommet når rakettens hastighet har overkommet planetens unnslippingshastighet.
5. Vi må vite hva posisjonen vår er i det vi er i verdensrommet.
Vi har gjort en forenkling her. Nemlig at vi ser bort i fra luftmotstand. Vi kommer til å gjøre beregninger senere der vi tar med luftmotstand, men ikke enda.
Vår planet har en rotasjonshastighet som vil gi oss en initialhastighet i y-retning. Se for deg at du skal kaste en kule så langt du klarer. Hvordan ville du gjort det? Ville du støtet den fra deg som en kulestøter, eller ville du snurret rundt og sluppet den som en diskoskaster? Det er "diskosprinsippet" (ikke et vitenskapelig anerkjent prinsipp på Jorda, men på vår planet er det vi som lager reglene) vi skal bruke.

Kilde: wikipedia
Tenk på dette en gang til: Vi kommer til å utnytte at planeten vår roterer. Hvordan? Jo, følg med nå. Har du noen gang stått på en karusell?
Hvis karusellen snurrer og du hopper av, så vil du bli slengt litt framover før du lander. Kanskje ikke så overraskende. Vi trenger å vite hvor fort vi beveger oss i y-retning i det vi tar av for å vite hvor vi havner når vi når verdensrommet. Tenk nå på bevegelseslikningene du har lært om i Fysikk 1. Husker du da at \(v=\frac{s}{t}\) , hvor \(v\) er fart, \(s\) er strekning og \(t\) er tiden? Dette gjelder ved konstant fart.

Hvis vi ser på et tverrsnitt av planeten vår, altså som vist på Figur 1, så ser vi at raketten vår befinner seg på ekvatorlinjen til planeten. Dette er det punktet lengst vekk fra sentrum i planeten. For å få \(v\) størst mulig, må vi ha \(s\) størst mulig. Altså, må strekningen vi reiser per tid være størst mulig. Planeten vår har en radius \(r=7605.752\) km. Hvis du nå ser for deg en kule igjen. Den snurrer med konstant fart. Hvis du står på nordpolen til kula og tar et lite skritt ut, så begynner du å sirkle rundt nordpolen. Radiusen fra linja gjennom polene til der du står er mindre enn radiusen til selve kula.
Altså må du befinne deg på ekvatorlinja med lengst avstand til rotasjonsaksen. Dermed blir initialhastigheten vi får i positiv y-retning,
\(v_0=\frac{2\pi r}{P}\)
hvor \(P\) er rotasjonsperioden til planeten vår om sin egen akse, eller en dag, som vi kaller det. Den den er 1,14 ganger en dag på Jorda (se tabellen her). Det gir
\(\begin{align*} P&=1.14\cdot24\cdot60\cdot60=98496\,s\\ \Rightarrow v_0&=\frac{2\pi\cdot7905750\,m}{98496\,s}\\ &\approx 504.32\,m/s \end{align*}\)
La oss nå presentere våre resultater på en simulert testoppskytning av raketten vår.
| \(v_{esc}\) | \(m_{tot}\) | \(N_p\) | \(N_b\) | \(F_R\) |
| \(1.23\cdot10^4km/s\) | \(5100\,kg\) | \(10^5\) | \(1.6\cdot10^{13}\) | \(4.4\cdot10^4N\) |
\(m_{tot}:\) total masse. Romskip: 1100 kg, drivstoff: 4000 kg
\(N_p:\) antall partikler per boks
\(N_b:\) antall bokser
\(F_R:\) Thrust fra raketten
Dette gir dette resultatet:
| Tid | Drivstofforbruk | Drivstoff igjen |
| \(835.77s\) | \(3525.71kg\) | \(474.23kg\) |
Vi bruker altså 13.92 minutter på å nå unnslippingshastighet. Da har vi 474.23 kg drivstoff igjen. Dette er drivstoff vi vil bruke på å navigere i verdensrommet, og til å bremse landingen når vi skal lande på en fremmed planet.
I følge simuleringene vår skal vi klare å nå unnslippingshastighet før vi går tom for drivstoff. La oss bare si at dette har vært veeeldig vanskelig. Vi har brukt utrolig mye tid på å prøve å finne ut av hva som er galt. Vi anser oss selv til å være relativt kompetente når det kommer til grunnleggende matematikk, men vi har faktisk hatt diskusjoner om hvordan vi regner ut arealet av et kvadrat når sidene har verdier under 1. Men nok gråting fra vår side, over til hvordan vi har tenkt.
1. Først brukte vi Newtons 2. lov for å finne akselerasjonen.
\(\sum F = ma\)
Her må vi brukte vektorer, for å passe på at retningene blir riktig. Vi kaller \(\hat{r}\) enhetsvektoren i radiell retning ut fra planetens sentrum. Den er definert slik
\(\hat{r}=\frac{\vec{r}}{|\vec{r}|}\)
Når vi gjør dette, får vi en vektor med lengde 1, som peker i radiell retning. Da blir Newtons 2. lov på vektorform slik
\(\sum\vec{F}=m\vec{a}\,\hat{r}\)
Grunnen til at vi kan holde oss til radiell retning er at akselerasjonen alltid virker i negativ radiell retning. Thrusten (skyvkrafta) fra raketten virker alltid i positiv radiell retning under takeoff. Videre blir
\(\sum\vec{F}=\vec{F}_{thrust}\hat{r}-\vec{F}_G\hat{r}=m\vec{a}\,\hat{r}\)
Vi løser for \(\vec{a}\), og får
\(\vec{a}=\frac{\vec{F}_{thrust}-\vec{F}_G}{m}\)
For å gjøre dette enda mer komplisert må vi se på masse som funksjon av tid. Vi mister masse hele tiden, på grunn av drivstofforbruket. Da blir uttrykket slik
\(\vec{a}=\frac{\vec{F}_{thrust}-\frac{Gm(t)M}{r^2}}{m(t)}\hat{r}\)
Dette er akselerasjonen vår. Litt av et uttrykk. Okey, moving on.
2. Vi bruker Euler-Cromer til å løse likningssystemet. Nok en utmerket metode vi har hentet fra Jorda. Kort fortalt blir det seende slik ut
\(\begin{align*} \vec{a}_i&=\frac{\vec{F}_{thrust}-\frac{Gm_iM}{r^2}}{m_i}\hat{r}\\ \vec{v}_{i+1}&=\vec{v}_{i}+\vec{a}_i\cdot dt\\ \vec{r}_{i+1}&=\vec{r}_i+\vec{v}_{i+1}\cdot dt\\ t_{i+1}&=t_i+dt\\ m_{i+1}&=m_i-massetap\cdot dt \end{align*}\)
Det er algoritmen sin, tenker jeg! Vi oppdaterer også hele tiden \(\hat{r}\) ved å hente ut det i'te elementet til \(\vec{r}\) og løse som forklart over. Det neste vi trenger er å finne ut av hvor i solsystemet vi er. Hittil har vi jo bare sett på posisjon fra planeten. Dette løser vi med vektorregning.
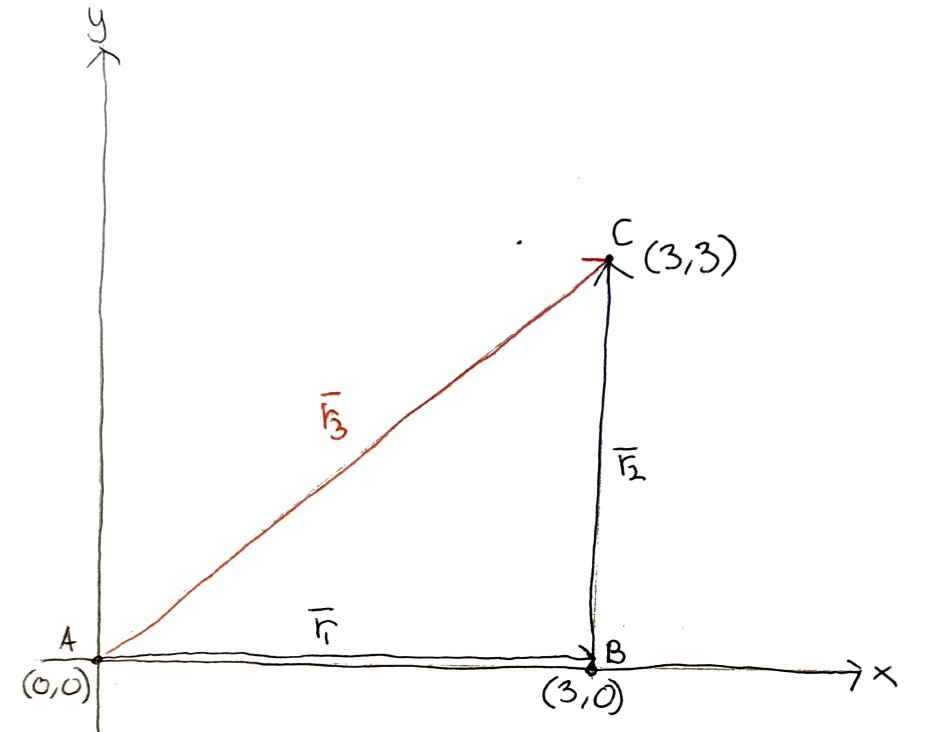
Se på Figur 2. Vi står i punktet A, som ligger i (0,0). Så går vi til B, som ligger i (3,0). Deretter går vi til C, som ligger i (3,3). Vektorene blir da
\(\begin{align*} \vec{r}_1&=B-A=(3,0)-(0,0)=(3,0)\\ \vec{r}_2&=C-D=(3,3)-(3,0)=(0,3)\\ \Rightarrow\vec{r}_1+\vec{r}_2&=(3,0)+(0,3)=(3,3) \end{align*}\)
Vi kan altså legge til (og trekke fra) vektorer som ligger etter hverandre, for å komme fra til det punktet vi ønsker.
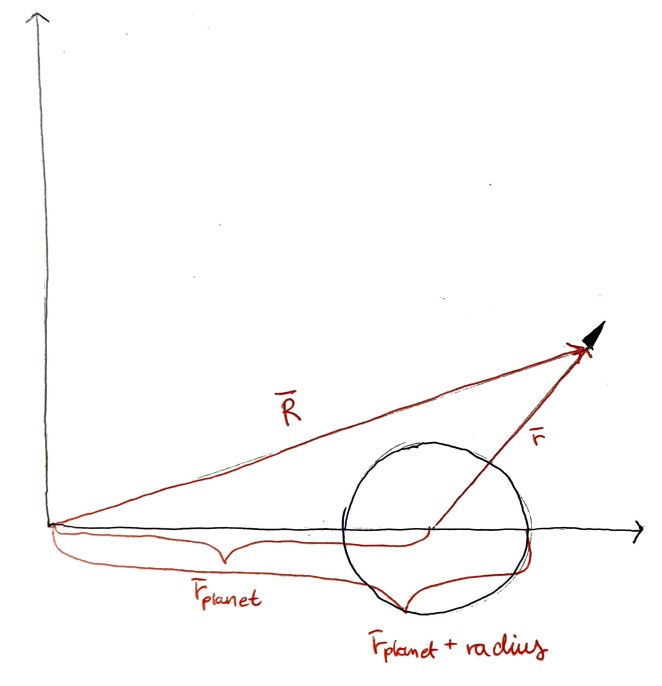
Se nå på Figur 3. Her kan vi gjøre akkurat det samme. Vi har posisjonen til oppskytingspunktet, avstanden fra stjernen til planeten, og vi har beregnet hvor raketten vil være etter at den har nådd unnslippingshastighet. Tabellen under viser hva vi vet, og hva vi har funnet.
| Radius | Avstand til stjerne | Rakettposisjon | Posisjon i forhold til stjerne |
| \(7605.75km\) | \(1.8589AU\) | \(\Big[2.781\cdot10^{11},2.548\cdot10^7\Big]km\) | Dette har vi dessverre kalkulert feil =( |
Vi ser at kalkulasjonene våre ikke stemmer, fordi posisjonen til raketten i systemet sett fra planeten er identisk med den utregnede posisjonen i systemet sett fra stjernen. Dette kan handle om at vi har noen verdier gitt i AU, og noen i km. Konverteringen mellom disse kan ha gått galt, eller vi kan ha regnet feil.
Men, vi har ikke kommet helt hit bare for å gi oss! Vi skal prøve likevel!
Oppskytning
Vi har stroppet oss fast og har mission control på ørene våre. En svetteperle kan kjennes gli nølende nedover ryggen. Til høyre for meg sitter Anton. Han gir meg tommelen opp. Blikkene våre er alvorspreget.
"Take off in 10..."
Hvorfor snakker de på engelsk? Språket vårt her likner mer norrønt.
"9..."
Setene begynner å riste. Adrenalinet stiger mens vi sjekker at alle instrumentene fungerer.
"8.."
Søren, har jeg husket å skru av kaffetrakteren?
"7... 6... 5..."
Vi er koblet fra rampen og en grå røyk bølger oppover vinduet. Boosterene har startet og vi kan så vidt merke at vi blir trykket ned i setene.
"4... 3... 2..."
Vi føler oss tunge. Godt vi ikke dro på byen i går.
"1..."
Det er tungt å puste. Kroppen er blytung.
"We have liftoff!"
Vi borer oss gjennom lufta og opp mot stjernene. Instrumentpanelet sier at vi har en akselerasjon på litt over 8 m/s2. Raketten rister og det bråker noe voldsomt. Heldigvis har vi forsikret alt om bord.
"Whitney, we have a problem"
Det er stemmen til Anton som spraker inn i øret mitt. Jeg ser bort på han og han peker på bensinmåleren. Den synker voldsomt fort. For fort. Vi visste at beregningene våre ikke stemte helt, men dette er hinsides all forventning. Foran meg har jeg noen spaker og ved siden av dem en stor rød knapp. "Manual override". Vi har ikke råd til å miste raketten, så vi installerte noen modifiserte koder fra Need for Speed og Grand Theft Auto. Med disse skal vi kunne nødlande.
Slaget er tapt. Vi er tomme for drivstoff. Foran oss ser vi ikke lenger stjernene, men steinene. På bakken. Vi har utløst fallskjermen og vi styrer snuta opp for å få en mykere landing.
På bakken igjen. Tilbake til tegnebrettet. Vi gir oss ikke så lett.
Med disse nye parameterne skal vi klare det.
| Lengde boksside | T | \(N_p\) | Str. på bokshullet | Drivstoff |
| \(5.0\cdot10^{-7}m\) | \(3\cdot10^3K\) | \(250\cdot10^3\) | \(2.5\cdot10^{-7}m\) | \(2.8\cdot10^{4}kg\) |
Vi sitter nok en gang i raketten. Lang historie kort:
VI KLARTE DET! Vi er i verdensrommet! Hurra! Jeg og Anton fistbumper og tar bølgen oss i mellom. Men vi har et problem. Vi vet ikke hvor vi er. I følge mission control har vi et avvik fra vår nye beregnede sluttposisjon med \(8.83\cdot10^{-5}AU\). Med andre ord, vi er lost in space. Da kan vi bruke tiden på noe nyttig.
Neste innlegg vil handle om planetbaner og Kepler. Husker dere Keplers lover? Vi skal bruke disse og mye mer framover.
Forrige innlegg << Neste innlegg >>
