Når vi befinner oss nærme en planet, kan vi med stor sikkerhet si at gravitasjonskreftene fra planeten er større enn fra stjerna. For ja, det vil virke krefter fra stjerna på romskipet vårt. Grunnen til at vi vil se nøye på dette er at det vil ha mye å si for oss når vi skal inn i orbit (gå i bane rundt planeten). Vi vil også vite hvor nærme vi må være planeten for at vi skal kunne ta bilde av den med kameraet vårt. Vi starter med en antagelse om at gravitasjonskreftene fra planeten er \(k\) ganger større enn kreftene fra stjerna. Det vil være enklere å utføre en orbital injection maneuver (innflyvning til å gå i bane) ved høye verdier for \(k\). Derfor er det lurt å finne et uttrykk for avstanden vi befinner oss i, uttrykt ved avstanden fra stjerna og \(k\).
Vi har at
\(\vec{F}_*=\gamma \frac{M_*m_R}{|\vec{r}|^2}\)
er gravitasjonskreftene fra stjerna på massen til raketten \(m_R\) når den befinner seg ved en avstand \(|\vec{r}|\) fra stjerna \(\left(|\vec{r}|=\sqrt{x^2+y^2+z^2}\right)\). \(M_*\) er som vanlig massen til stjerna, og \(\gamma\) er Newtons gravitasjonskonstant.
Videre er
\(\vec{F}_p=\gamma \frac{M_pm_R}{|\vec{l}|^2}\)
gravitasjonskreftene fra planeten på raketten når den befinner seg ved avstanden \(|\vec{l}|\) fra planeten. \(M_p\) er planetens masse. Vi antok at \(\vec{F}_p\) er \(k\) ganger større enn \(\vec{F}_*\). Vi vil ha følgende situasjon, illustrert nedenunder.
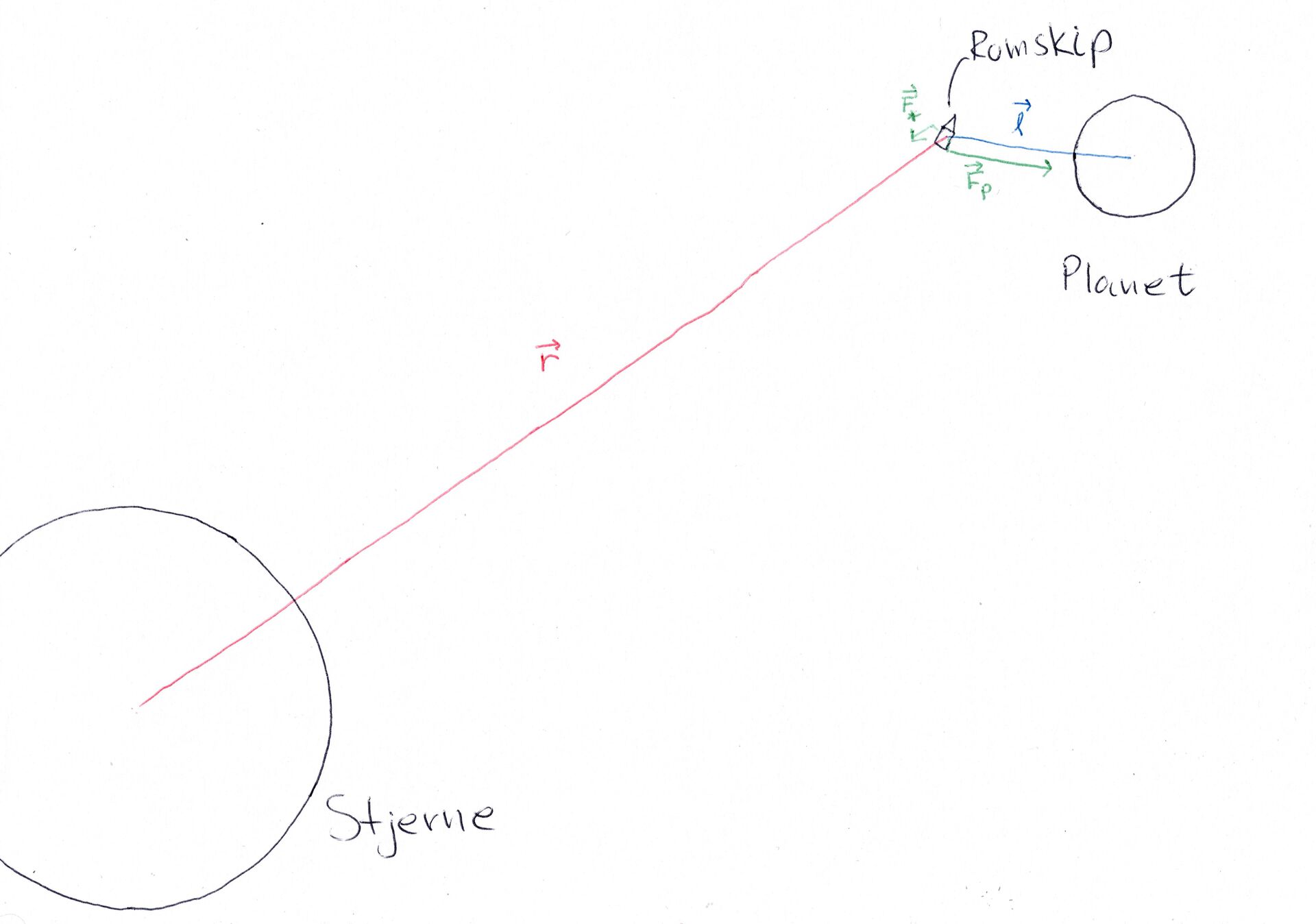
Fra Figur 1 ser vi at \(\vec{F}_*\) virker i radiell retning mot stjerna, og at \(\vec{F}_p\) virker i radiell retning mot planeten. Vi ønsker altså å finne et uttrykk for avstanden \(l=|\vec{l}|\) fra planeten til romskipet vårt. Ved antagelsen vår får vi følgende.
\(\begin{align*} \vec{F}_p&=k\cdot\vec{F}_*\\ \gamma\frac{M_pm_R}{l^2}&=k\cdot\gamma\frac{M_*m_R}{|\vec{r}|^2}\\ \frac{M_p}{l^2}&=\frac{k\cdot M_*}{|\vec{r}|^2}\\ l^2&=\frac{|\vec{r}|^2M_p}{k\cdot M_*}\\ l&=|\vec{r}|\sqrt{\frac{M_p}{k\cdot M_*}} \end{align*}\)
Det vi egentlig har gjort nå er å finne et uttrykk for avstanden til planeten gitt et forhold mellom gravitasjonskreftene fra stjerna og planeten. Vi ser at jo større \(k\) blir, jo mindre blir radikanden (tallet som står under rottegnet), jo mindre blir roten. Planetens masse er mye mindre enn stjernas masse, så tallet blir også mye mindre enn 1. Avstanden \(|\vec{r}|\) blir større og større jo lenger unna stjerna vi kommer, men vi skalerer med et veldig lite konstant tall. Dermed har vi god kontroll på avstanden vi har fra planeten.
Nå skal vi se på kameraet vi har med oss. Det har en pikseloppløsning på \(P\times P\). Altså vil vi ha et rutenett av piksler som vist på figuren under.
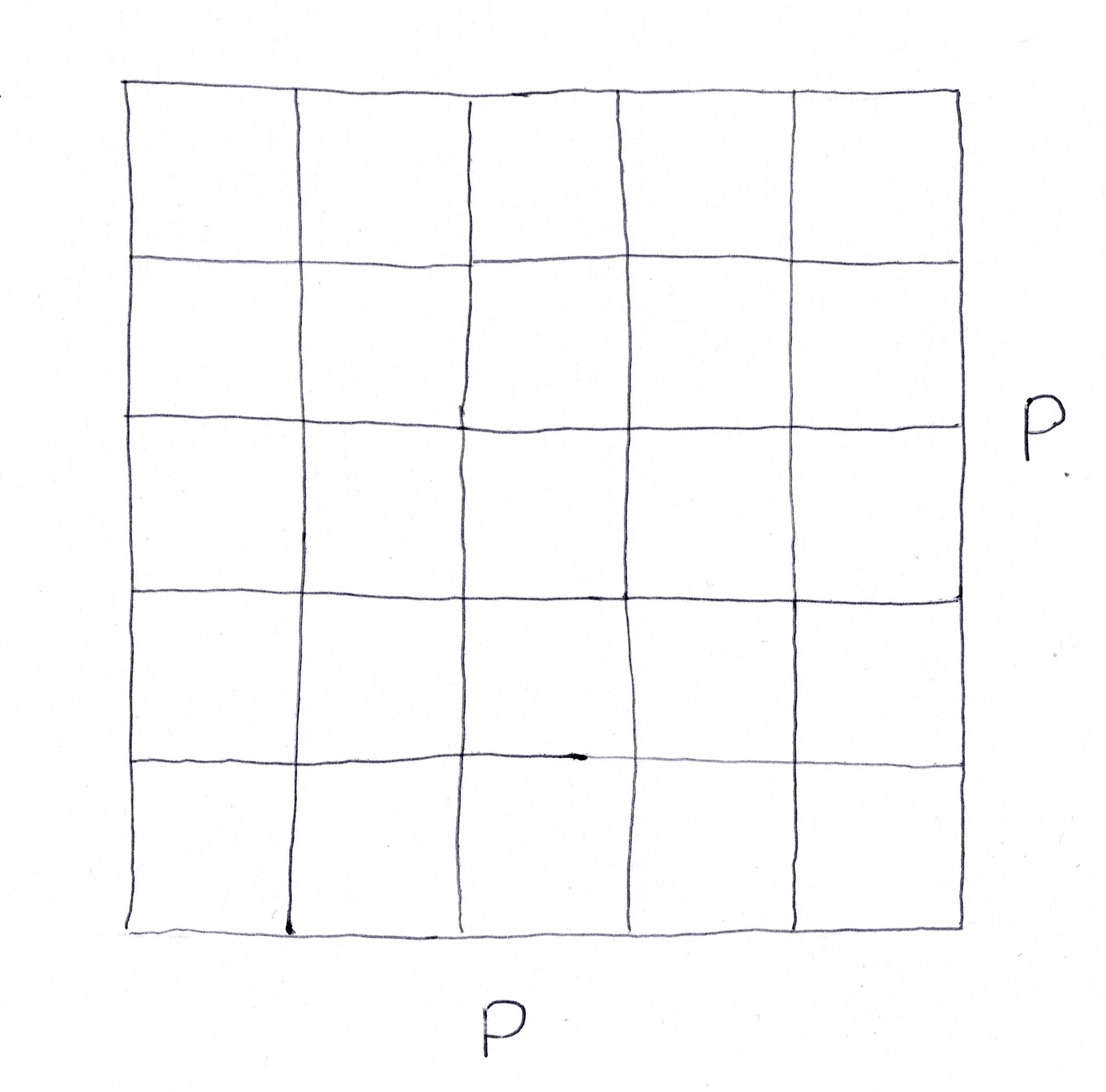
Et objekt sies å være oppløst (synlig på et fotografi) når det fremkommer på mer enn 1 piksel på det resulterende bildet. Dette legger grunnlag for at vi trenger at planeten fremkommer på minst 2 piksler hver vei.
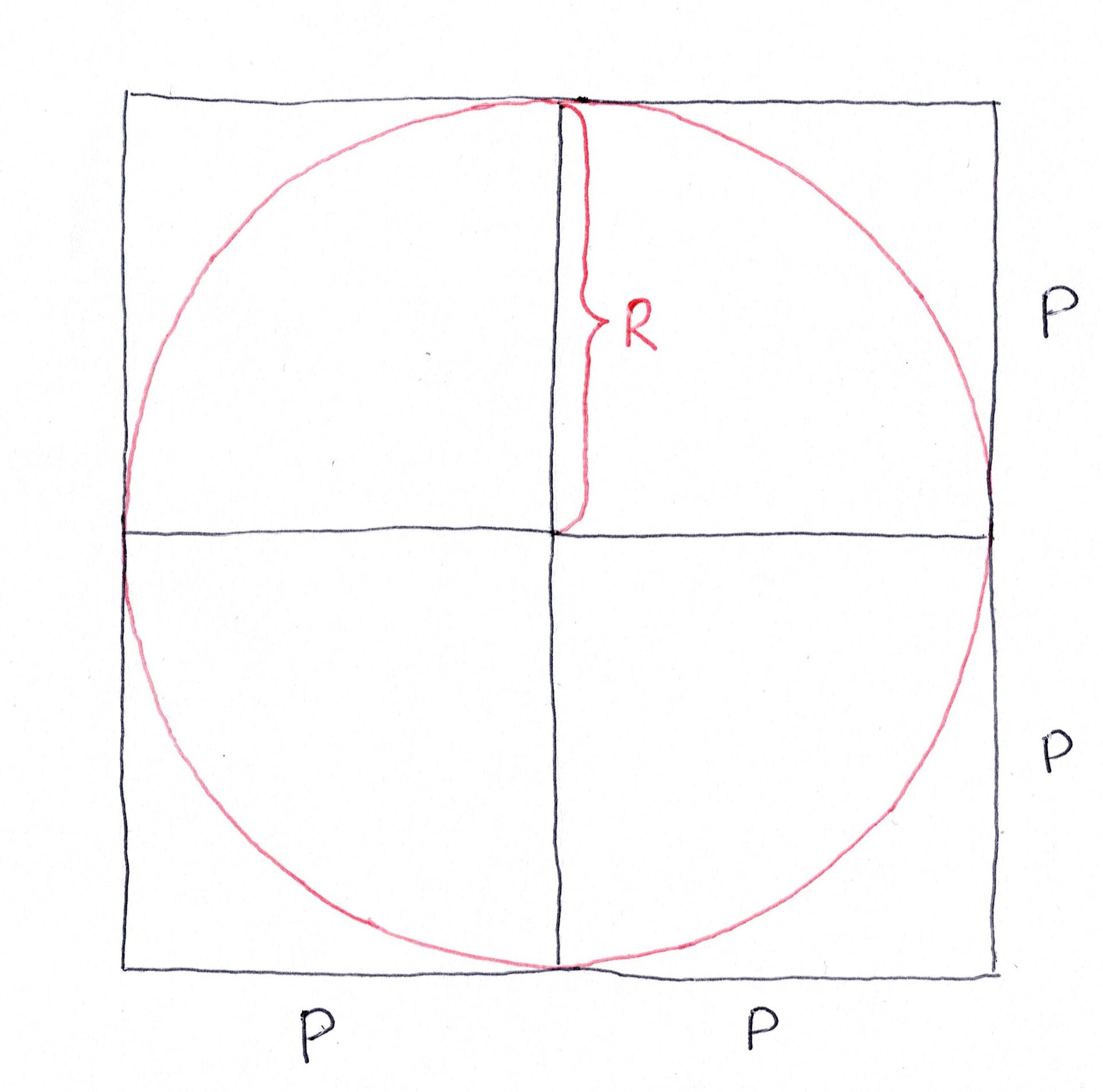
Det første vi merker oss fra Figur 3 er at radien til planeten må dekke minst 1 piksel hver vei. Vi har også en vinkeloppløsning på \(F\times F\) grader. Det vil si at vi får et synsfelt på \(F\) grader hver vei.
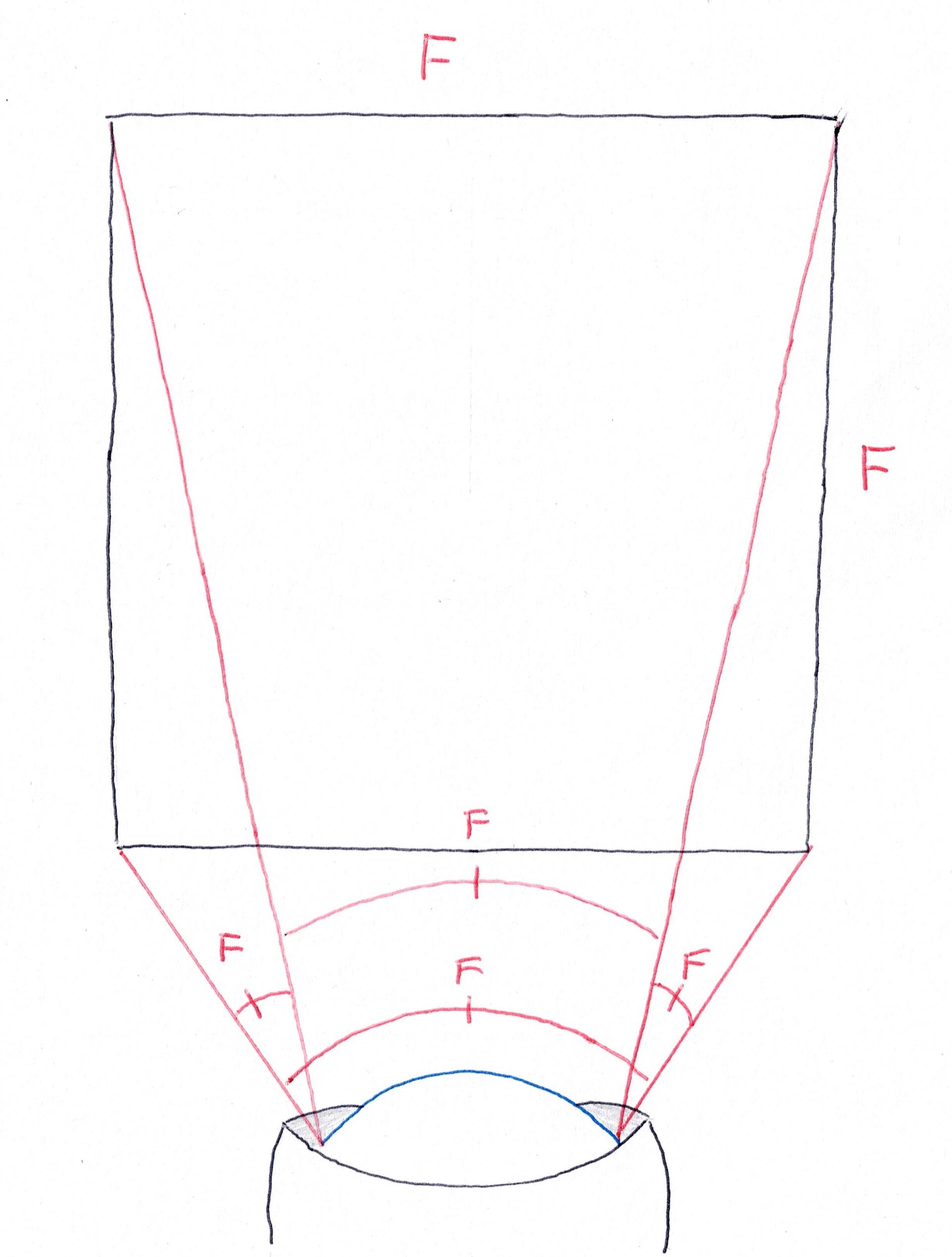
Nå må vi tenke oss om. Hvordan kan vi finne ut av hvor nærme vi må være planeten for å kunne ta et oppløst bilde av den? Se på figuren under.
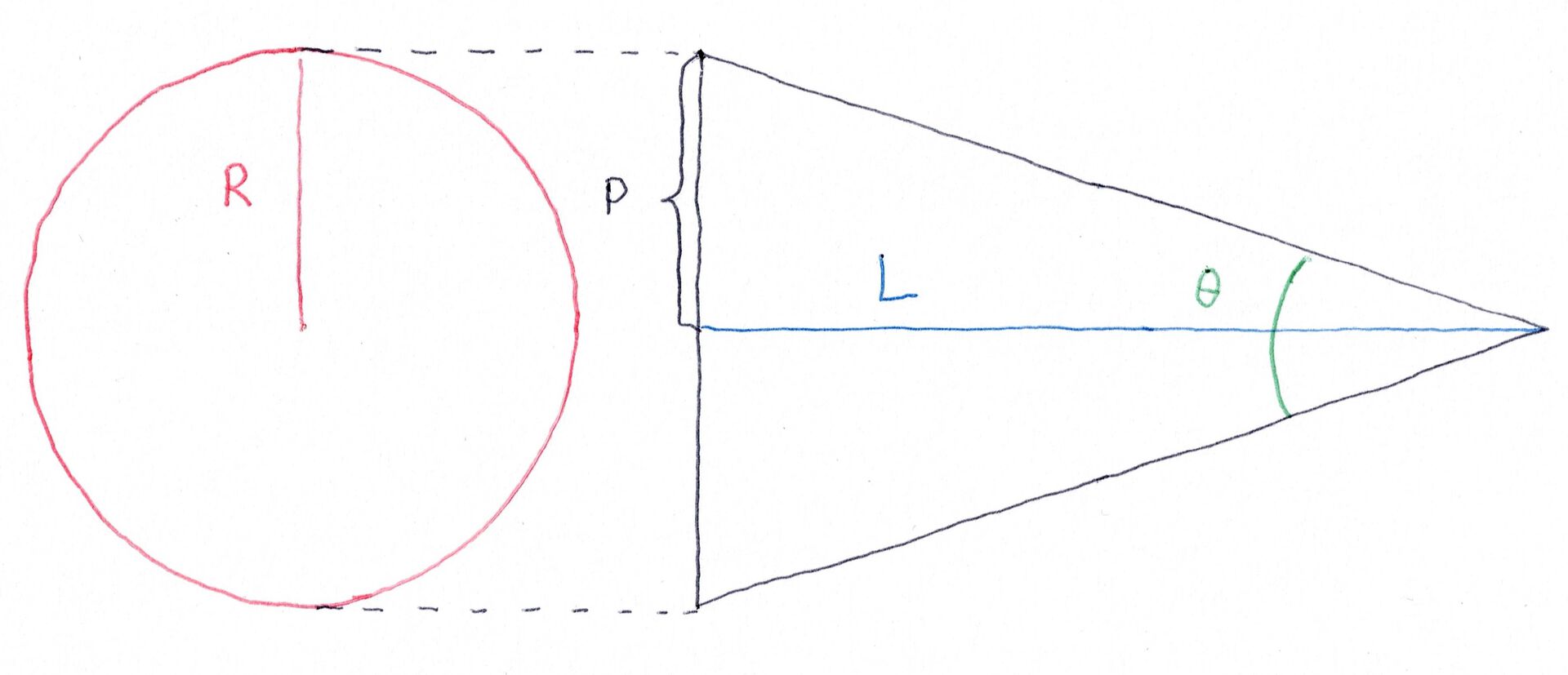
\(L\) er avstanden fra kameraet (og romskipet, så klart) til planeten, \(R\) er radius til planeten og \(P\) er 1 piksel. Vinkelen \(\theta\) blir altså vinkeloppløsningen \(F\) delt på antall piksler vi ser på. Vi har altså at hele planeten må dekke 2 piksler, så halve planeten må dekke 1 piksel. Eller, sagt på en annen måte, radius til planeten må dekke 1 piksel. Da blir vinkeloppløsningen per piksel lik \(\frac{F}{P}\). Nå er det klart for litt trigonometri.
Husker dere de trigonometriske funksjonene? Ja, helt riktig, sinus, cosinus og tangens. Men hva var nå de igjen?
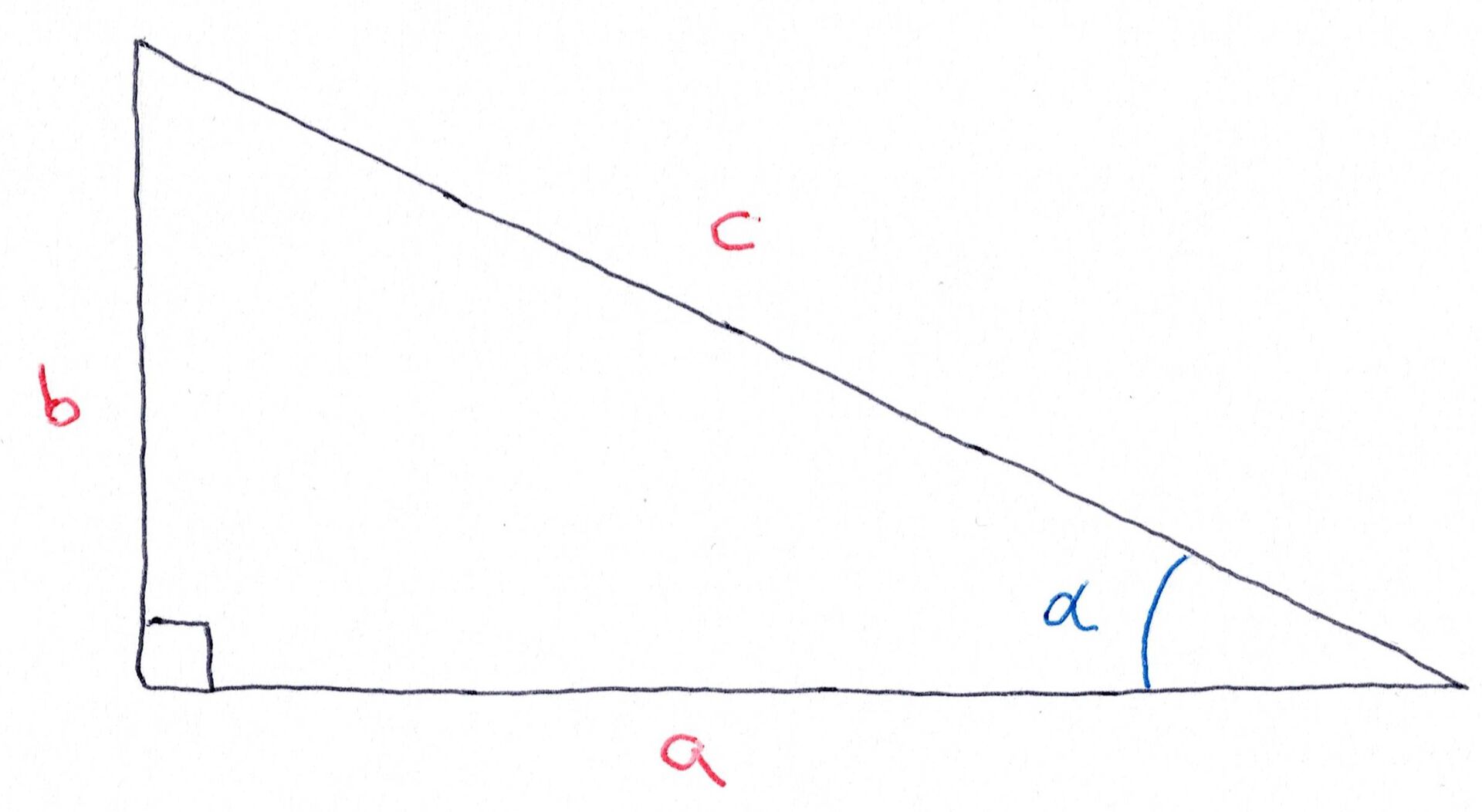
De to sidene som utgjør den rette vinkelen kalles kateter. Den tredje siden kalles hypotenusen. Pythagoras setning sier at katet i andre pluss katet i andre er lik hypotenus i andre. Men vi kan også bruke vinkelen \(\alpha\). Da har vi
\(\begin{align*} \frac{b}{c}&=\sin{\alpha}\\ \frac{a}{c}&=\cos{\alpha}\\ \frac{b}{a}&=\tan{\alpha} \end{align*}\)
Som dere ser i Figur 5, blir \(R=b\) og \(L=a\). Vinkelen \(\alpha\) blir \(\frac{F}{P}\). Da kan vi sette inn verdiene. Vi får
\(\begin{align*} \frac{R}{L}&=\tan{\frac{F}{P}} \end{align*}\)
Vi kommer ikke til å bevise det her, men \(\tan{x}>x\). Altså må
\(\begin{align*} \frac{R}{L}&=\tan{\frac{F}{P}}>\frac{F}{P}\\ \frac{R}{L}&>\frac{F}{P}\\ \frac{L}{R}&<\frac{P}{F}\\ L&<\frac{RP}{F} \end{align*}\)
Her har vi et fint uttrykk for hvor nærme vi må være planeten for å kunne ta et kult bilde! Takk for denne gang.