Koordinatsystem på kuleform
Jeg vet at å begynne å snakke om koordinatsystemet nå kan virke litt umotivert, men det kommer til å gi mening for deg etterhvert. Vi har nemlig en helt genial satellitt i bane om planeten vår, som har tatt bilder av verdensrommet. Disse bildene kommer vi til bruke senere til å finne ut av hvor i verdensrommet vi befinner oss, men da må vi gjøre litt forhåndsarbeid her nå.
- Antakelse: Siden stjernene på himmelen er veldig langt unna oss, kan vi først anta at himmelbildet er konstant. Det vil si at bildet vi ser av himmelen ikke vil endre seg med det første, før det har gått veldig lang tid. Dermed kan vi generere referansebilder i dette innlegget som vi kan bruke til å orientere oss med i neste innlegg.
Dermed kan vi se for oss at bildet av verdensrommet ligger rundt oss som en slags himmelkule (bokstavelig talt en kule med bildet av verdensrommet på), og det er derfor vi skal snakke litt om koordinatsystemer.
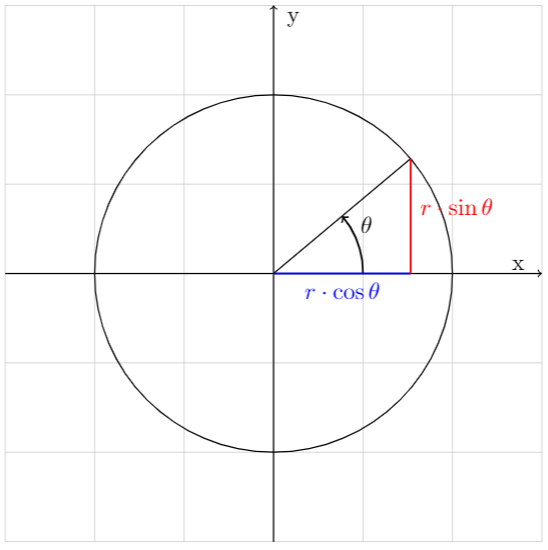
Det er kanskje kjent for deg at det finnes flere koordinatsystemer enn det kartesiske (med x og y-koordinater) eller ikke. En av de mest vanlige er polare koordinater, som du kanskje gjenkjenner fra enhetssirkelen og kan skrives slik:
\(x = r\cdot\cos(\theta)\)
\(y = r\cdot\sin(\theta)\)
Som lager en sirkel avhengig av \(r\) og \(\theta\). Men vi kommer til å trekke dette konseptet litt lenger, og se på noe som kalles for sfæriske koordinater også kalt kulekoordinater. Det betyr (som det ligger litt i ordet) at vi tar med oss denne ideen til 3D-rommet, og bruker koordinater som avhenger av nye variabler som vi kaller \(r,\;\phi,\;\theta\) som illustrert i figur 2, til å skrive koordinater sfærisk.
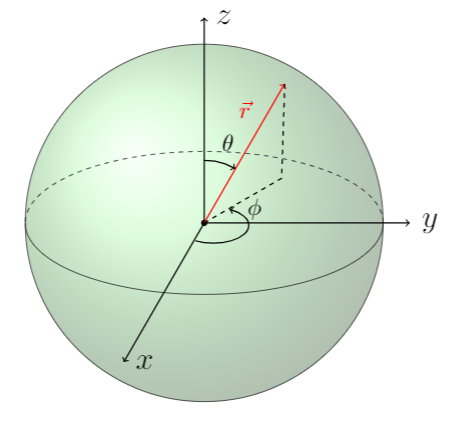
På denne måten kan vi kontrollere hvilket utsnitt av himmelen vi ønsker å se på ved hjelp av vinkler, som viser seg å være ganske nyttig. I figur 2 brukes parameteriseringen
\(\vec{r} = (x,y,z)\)
\(x = r\cdot\cos(\phi)\sin(\theta)\)
\(y = r\cdot\sin(\phi)\sin(\theta)\)
\(z = r\cdot\cos(\theta)\)
der hvor \(\phi\in[0, \pi],\;\theta \in [0, 2\pi)\) og \(r\) er radien til kula. Denne parameteriseringen er den vi bruker videre også, med noen små modifikasjoner som vi kommer til senere.
Jorda er flat! Og litt utstrukket..
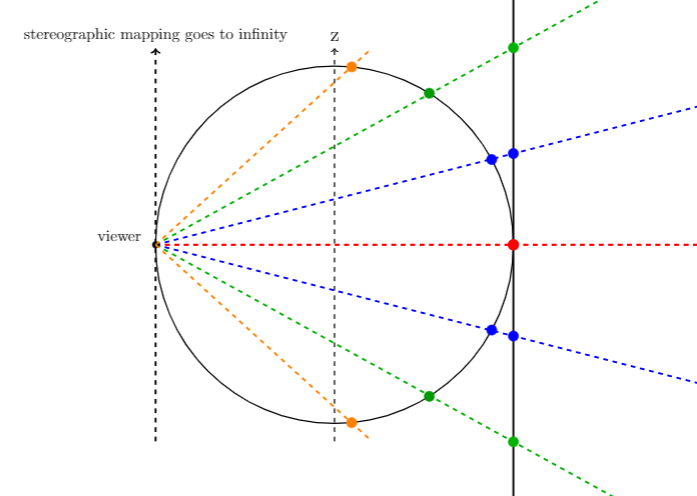
Nei vi er ikke konspirasjonsteoretikere, ikke gå! Vær så snill å fortsett å lese! Dette er ikke surr skjønner du, jeg skal komme til poenget. Nå som vi har dette himmelkuleskallet vårt, så trenger vi en måte å få dette himmelbildet ned på et flatt vanlig bilde, slik at vi kan finne ut av hvor vi er. Det finnes flere måter å mappe på, men metoden vi skal bruke kalles for stereografisk projeksjon, som er et mye vanskeligere ord enn metode. Prinsippet går ut på at vi som observatør i projeksjonspunktet trekker linjer fra der vi observerer gjennom et kuleskall og inn på flaten vi skal mappe på, som vi fritt kan velge selv. Altså finner vi oss et punkt vi står på, trekker linjer gjennom et kuleskall og videre gjennom en flate vi velger oss, og setter bildet/pikslene på skjæringspunktet på kuleflaten til å være pikslene/bildet på skjæringspunktet på flaten. Dette gjør vi til hele kuleskallet har blitt projisert på flaten, dvs. alle punkter på kuleskallet, og vi sitter igjen med en stereografisk projeksjon. Det finnes forskjellige egenskaper for de ulike flatene vi projiserer på gjennom denne metoden, som for eksempel kan være at vi ikke får med oss punktet vi observerer fra, om størrelser er bevart, om vinkler er bevart etc.
Jorda som eksempel
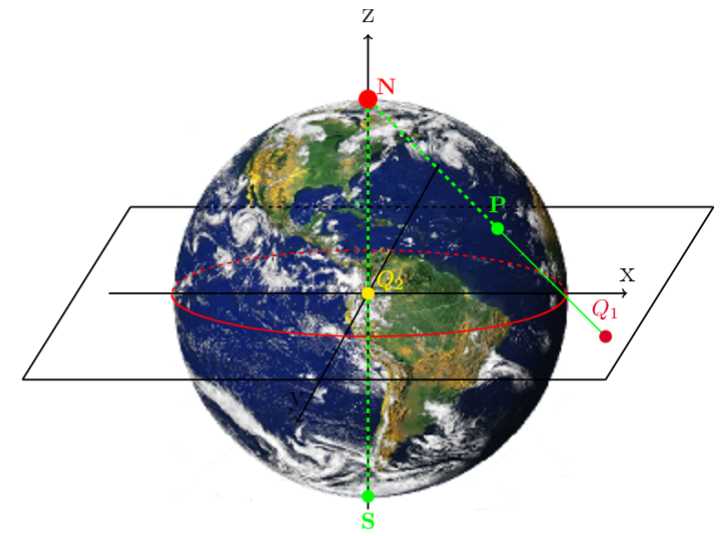
La oss bruke jorda som eksempel, siden mange kjenner til den. Det finnes mange morsomme flater vi kan projisere en kule på. For eksempel kan vi velge å projisere på xy-planet slik som i figur 4. Da velger vi for eksempel å stå på punktet N (nordpolen blir da projeksjonspunktet), og trekker linjer gjennom kulen, skjærer kuleflaten et sted, videre mot planet, og skjærer gjennom planet. Punktet vi traff på kuleflaten plasserer vi nå på punktet vi traff på planet, og dermed har vi projisert! Resultatet av akkurat denne ser du nedenfor.
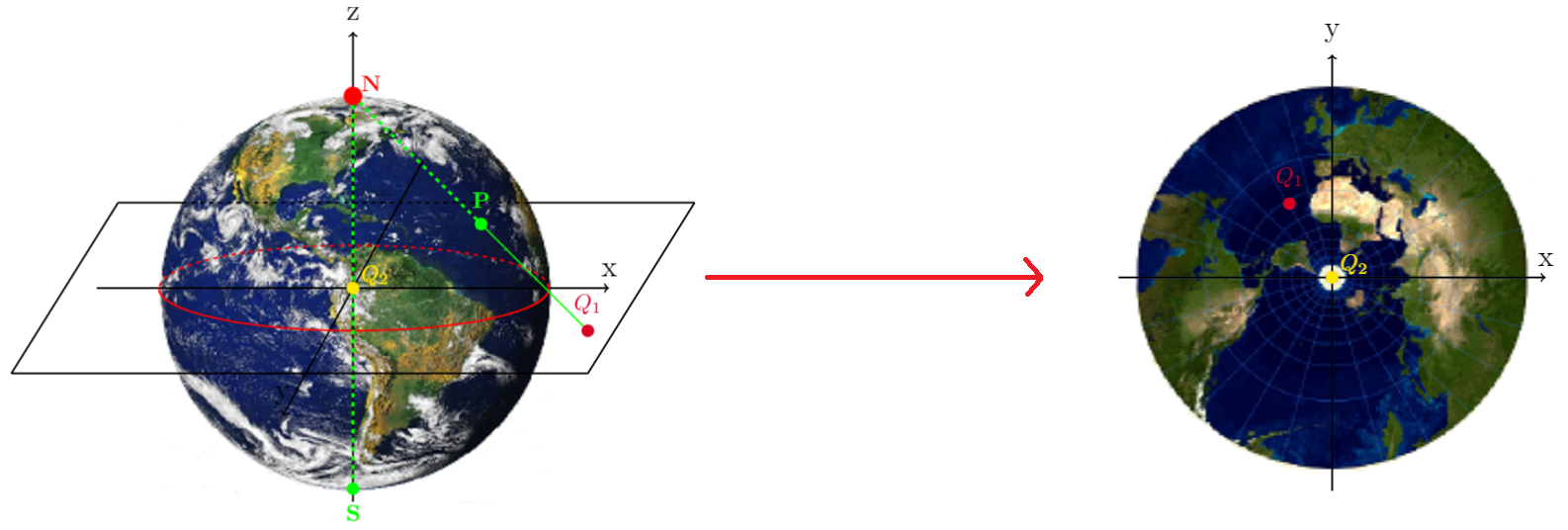
MERK: Hva skjer med nordpolen her? Er det mulig å projisere den gitt figurene ovenfor? Hva skjer med sørpolen? Er de virkelige størrelsene på landmassene bevart? Hva er forskjellen mellom under ekvator kontra over ekvator? Viktige spørsmål å tenke over.
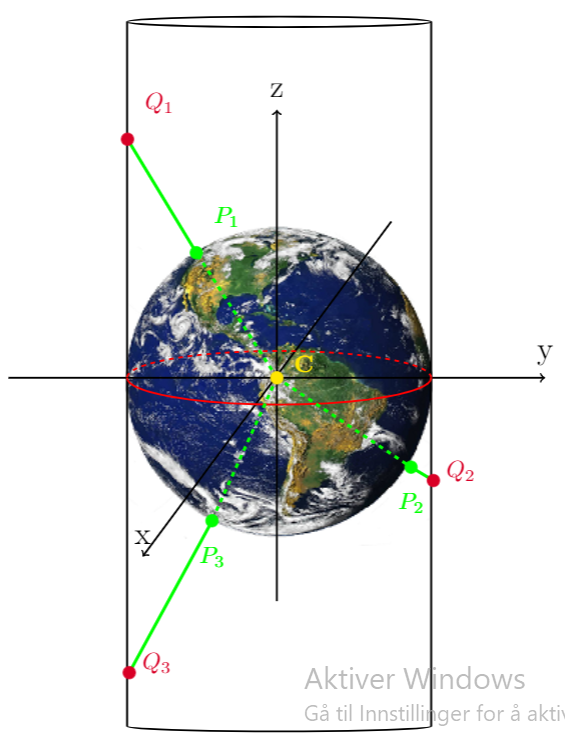
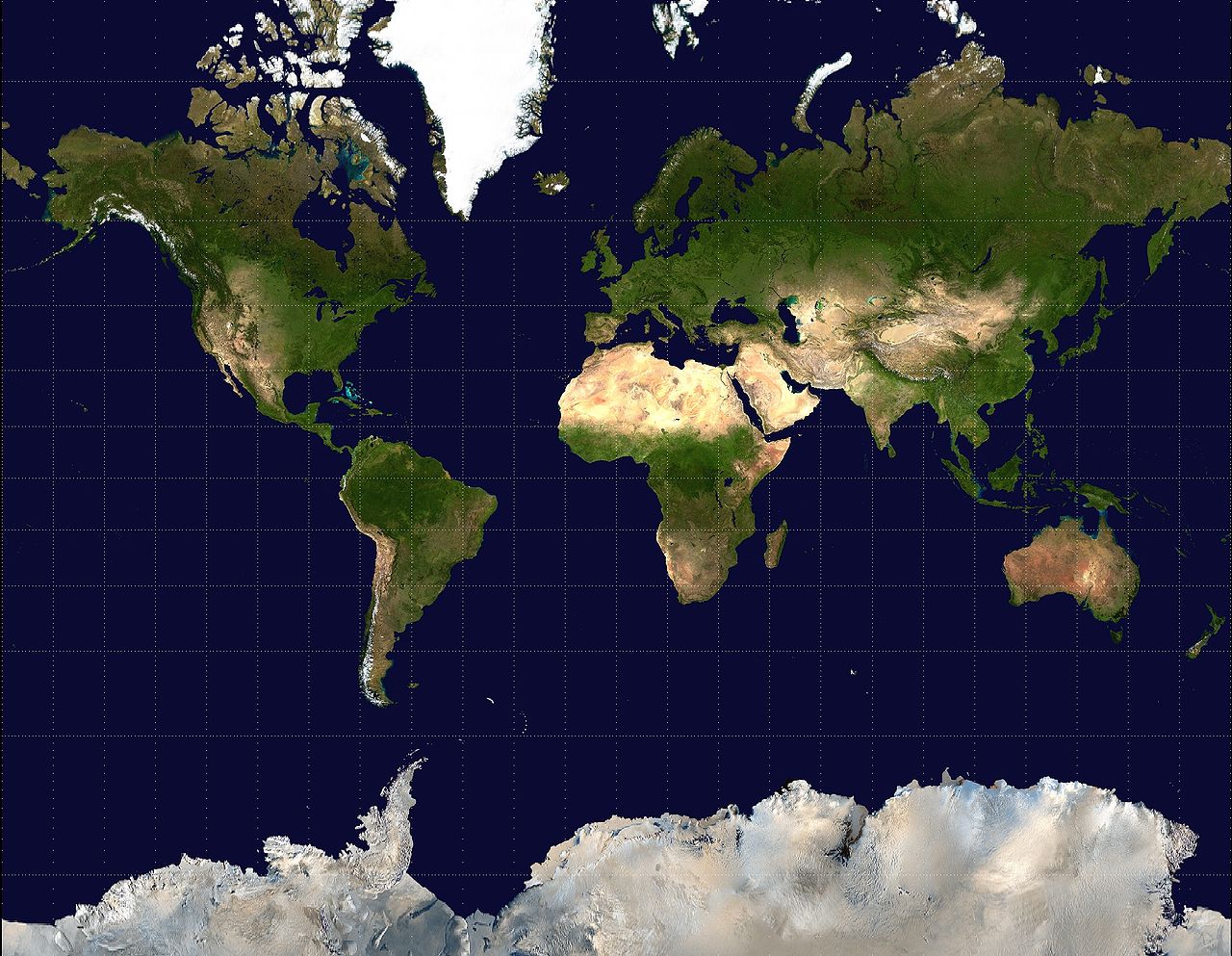
Vi kan også velge å projisere på en annen måte. Noen gang hørt om Mercator-projeksjon? Om du ikke har hørt om det, har du i alle fall sett det på verdenskartet! De aller fleste verdenskart er projisert på denne måten, som gjøres ved å legge en lang sylinder rundt jorda, slik som i figur 5. Det som er verdt å legge merke til her også er polene, og hvordan de blir projisert. Siden kartet lages ved å rulle ut rektangelet som binder rundt sylinderen, kommer polene til å være punkter som går mot uendelig. Derfor kan vi heller ikke se nordpolen, og punktene rundt kommer til å strekkes laaaangt ut. Det lages ofte egne kart for nordpolen og sørpolen, som ikke er en del av det normale verdenskartet. Dette kan gjøres ved å f.eks velge en flate som ligger tangent på polen vi ser på, slik at mest av størrelsen er bevart (seriøst, søk opp kart over polene på Google, tror de fleste mennesker aldri har sett det før). Effekten av utstrekningen er at landmassene også strekkes ut, slik at størrelsen på ulike land langs mot nord og sør blir større enn de skal være. Legg også merke til at eneste stedet som mappes helt korrekt er ekvator. Det finnes faktisk en nettside som heter thetruesize.com som illustrerer denne effekten, og er morsom å leke med (anbefaler å tulle med Russland, ser mye større ut enn det er!). Jeg legger til en siste illustrasjon av hvordan Mercator-projeksjonen kan se ut:
Vårt tilfelle av himmelkulen
Det har vært mye snakk om jorda nå, men la oss se på hvordan vi kommer til å anvende det i vårt tilfelle (som er hele grunnen til alt jeg forklarte ovenfor). Vi kommer til å befinne oss inne i sentrum av himmelkulen for enkelhets skyld. Vi bruker de sfæriske koordinatene fra tidligere til å velge ut hvor på himmelkulen vi skal se. Et lite problem som enkelt kan fikses, er at parameteriseringen alltid starter på samme sted slik den var ovenfor. Vi kan innføre en \(\theta_0\) og \(\phi_0\) som skal bestemme hvor på kulen vi starter å parameterisere. Da kan vi sentrere parameteriseringen på lik måte som vi sentrerer en funksjon. Ta funksjonen f(x) = x som eksempel. Bytter vi ut x med x - 3, vil vi få f(x - 3) = x - 3. Disse funksjonene ser like ut, men f(x - 3) er flyttet 3 enheter bort på x-aksen slik at f(x - 3) = 0 når x = 3, kontra x = 0 som for f(x) = 0. Da kan vi generelt si at dersom f(x) = x vil f(x - a) = x - a sentrere f(x) rundt punktet a. Samme prinsipp bruker vi på parameteriseringen, og dermed:
\(x = r\cdot\cos(\phi - \phi_0)\sin(\theta - \theta_0)\)
\(y = r\cdot\sin(\phi - \phi_0)\sin(\theta - \theta_0)\)
\(z = r\cdot\cos(\theta - \theta_0)\)
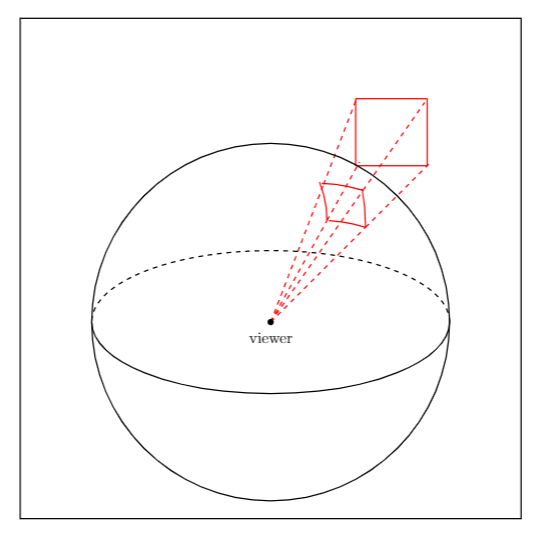
blir kulekoordinatene sentrert om \(\phi_0,\;\theta_0\). Vi har fortsatt noe mer å ta hensyn til: kameraet har begrenset FOV (field of view). Det er altså begrensningen på hvor mye kameraet vårt får med seg på et bilde, gitt i vinkler i x og y-retning. Jeg skal ikke gå veldig mye inn på FOV og hvorfor det begrenser bildet, og det står litt om det i denne setningen, men vit at bildet vi ser på er begrenset med en vinkel i polar (\(\theta\)) og asimutal (\(\phi\)) retning \(\alpha_{\theta}=\theta_{max}-\theta_{min}\) og \(\alpha_{\phi}=\phi_{max}-\phi_{min}\) som gjør at vi får et slags utsnitt av himmelen. Med andre ord får vi en slags utskjæring på himmelkulen som projiseres på en flate, som illustrert på figur 7.
Det jeg gjør nå er at jeg skal ta likningene for relasjonene mellom de sfæriske koordinatene og den stereografiske projeksjonen litt for gitt, og jeg kommer ikke til å forklare eller utlede dem. Likningene kan man vise med litt god algebra etc. men jeg bruker ikke tid på det her. Men jeg skal mer enn gjerne skrive dem ned for dere 😁:
\(X = \kappa\sin\theta\sin(\phi-\phi_0)\hspace{4.9cm}(1)\)
\(Y = \kappa(\sin\theta_0\cos\theta - \cos\theta_0\sin\theta\cos(\phi - \phi_0))\hspace{1.02cm}(2)\)
\(\kappa = \frac{2}{1 + \cos\theta_0\cos\theta + \sin\theta_0\sin\theta\cos(\phi-\phi_0)}\hspace{3.2cm}(3)\)
\(X_{max/min} = \pm\frac{2\sin(\alpha_{\phi}/2)}{1 + \cos(\alpha_{\phi}/2)}\hspace{4.65cm}(4)\)
\(Y_{max/min} = \pm\frac{2\sin(\alpha_{\theta}/2)}{1 + \cos(\alpha_{\theta}/2)}\hspace{4.75cm}(5)\)
\(\theta = \theta_0 - \arcsin\left[\cos\beta\cos\theta_0 + \frac{Y}{\rho}\sin\beta\sin\theta_0\right]\hspace{1cm}(6)\)
\(\phi = \phi_0 + \arctan\left[\frac{X\sin\beta}{\rho\sin\theta_0\cos\beta -Y\cos\theta_0\sin\beta}\right]\hspace{1.8cm}(7)\)
\(\rho = \sqrt{X^2 + Y^2}\hspace{6.18cm}(8)\)
\(\beta = 2\arctan\left(\frac{\rho}{2}\right)\hspace{6.06cm}(9)\)
Dette ser ut som hårete uttrykk, og det er ingen fare i å ikke vite hvor det kommer fra. Det er likevel veldig kjekt for oss å bruke, og derfor gjør vi nettopp det! Siden vi har en begrensning fra FOV med \(\alpha_{\phi},\;\alpha_{\theta}\) vil vi ikke lenger bevege og rundt hele kulen, med andre ord vil ikke \(\theta-\theta_0\in[0,\pi],\;\phi-\phi_0\in[0,2\pi)\). Det som skjer i stedet er at \(\theta - \theta_0,\;\phi - \phi_0\) vil ligge i intervallet mellom \(\alpha_{\phi},\;\alpha_{\theta}\), med andre ord vil
\(\theta - \theta_0\in\left[-\frac{\alpha_{\theta}}{2},\frac{\alpha_{\theta}}{2}\right],\;\phi - \phi_0\in\left[-\frac{\alpha_{\phi}}{2},\frac{\alpha_{\phi}}{2}\right]\), som er viktig at vi får med oss. Ideen videre her er å bruke et numerisk XY-grid, og så transformere koordinatene i XY-gridet til det sfæriske med likning (6) og (7) slik at vi kan hente piksler fra himmelkulen, og sette det sammen til et flatt bilde.
Stjernetitting - litt mer om metode og resultat
Nå syntes jeg det har vært utrolig mye snikk-snakk, uten at vi har noe bilde av verdensrommet. Jeg syntes det er på høy tid å forklare hvordan vi faktisk transformerer et bilde vi tar, så la oss gjøre nettopp dette. Vi skal generere et bilde fra himmelkulen og sammenlikne med et bilde vi allerede har tatt fra satellitten, for å sjekke om metoden vår fungerer. Verdiene vi bruker i første omgang vil være \(\alpha_{\theta} = \alpha_{\phi} = 70^\circ\), og \(\phi_0 = 0^\circ\), \(\theta_0 = 90^\circ\), siden det er der bildet fra satellitten er blitt tatt også. Vi tar det steg for steg:
- Vi finner størrelsen på bildet, som vil si antall piksler vi har i hver retning av bildet. Fra satellitten får vi at bildestørrelsen er på 640 x 480. Vi henter et bilde fra satellitten som vi kan sammenlikne med senere i samme sleng, og vi henter også ut himmelkulebildet fra satellitten.
- Vi gjør om alle grader til radianer, slik at det blir enklere å regne på. Forholdet mellom radianer og grader er \(1 \deg = \frac{\pi}{180}\text{rad}\).
- Vi lager et grid for \(X,\;Y\) på størrelsen 640 x 480 så det matcher satellittbildet, med uniformt fordelte verdier (fordi det er lett å jobbe med) som går fra \(X_{min},\;Y_{min}\) til \(X_{max},\;Y_{max}\), og implementerer relasjonene mellom \(\theta,\;\phi\) og \(X,\;Y\). Vi bruker så denne relasjonen (likning (6), (7) ovenfor) på \(XY\)-gridet til å lage et \(\phi\theta\)-grid. Vi looper gjennom \(\phi\theta\)-gridet og finner pikslene på himmelkulen som vi lagrer i en array, og bruker en modul i Python kalt Pillow til å generere et bilde ut ifra den nye dataen vi har lagret i arrayen. Resultatet av dette blir:


Suksess! Bildene ser helt like ut, og det er jeg fornøyd med (vi kunne kjørt en analyse for å teste men det kommer i neste innlegg). Neste mål nå blir å generere bilder slik at vi kan se hvordan det ser ut 360 grader rundt oss! Prosessen blir helt lik som beskrevet ovenfor, men denne gangen må vi sentrere bildet rundt forskjellige \(\phi_0\)-verdier. For å få godt nok antall bilder så vi har god nok oppløsning, tar vi ett bilde for hver grad, som betyr 360 (!) bilder der vi lar \(\phi_0 = 0^\circ,1^\circ,\dots,359^\circ\), mens \(\theta_0, \; \alpha_{\theta}, \; \alpha_{\phi}\) forblir de samme. Da vil vi kunne gjenkjenne hvor vi er i verdensrommet med \(1^\circ\) nøyaktighet senere (vi blir rundet til nærmeste hele grad, dvs. fra f.eks \(56.7^\circ\) til \(57^\circ\)). Vi lar programmet kjøre.. og kjøre.. og kjøre.. og kjøre.. og kjøre (50 minutter...). Resultatene er her, og vi åpner opp for å se som små barn en tidlig julaften morgen. Vi lager en animasjon som spiller av alle de 360 bildene grad for grad, og ender opp med dette resultatet:

360 x suksess! Dette ser utroooolig kult ut! Vi lagrer alle bildene så vi ikke trenger å kjøre koden som genererer dem mer, og neste steget blir å kjøre noen bildeanalyser slik at vi kan bruke resultatene våre her til å finne ut av hvor i verdensrommet vi befinner oss.