Basis av bilder
For å snakke om og analysere bilder, er det kanskje greit å vite noen standard ting om bilder først. Jeg snakket ikke noe særlig om dette i forrige innlegg fordi jeg ikke tenkte det var kjempebehov for det der, men det er litt viktigere i dette innlegget. Et bilde er bygget opp av piksler, se for deg bitte-bittesmå firkanter som ligger på for eksempel pc-skjermen eller mobilen din. Vi teller antall piksler langs X-aksen og Y-aksen, og skriver bildestørrelsen som X x Y. For eksempel kan vi ha et 300 x 120 bilde, som tilsvarer et rektangulært bilde som har større bredde enn høyde, dvs. 300 piksler bortover, og 200 piksler oppover. Alle disse små pikslene er det som til sammen danner bildet du ser på skjermen, i alle farger og detaljer.
Ja, hva med farger? Hver piksel har en verdi for enten rød, grønn, eller blå fargeverdier, som sier noe om hvor mye av den fargen som ligger i pikselen. Disse verdiene kan ligge mellom 0 eller 255, som sammen som en kombinasjon skal gi fargen i pikselen. Ofte er det representert i en tuppel, der første verdi er rød, andre er grønn, og siste er blå, altså RGB, eksempelvis som (255, 153, 51) (som blir denne fargen). Altså vil en kombinasjon av disse kunne gi oss alle fargene vi ser og trenger (siden hver R, G, eller B kan være 256 ulike tall, finnes det \(256^3 = 16\;777\;216 \) forskjellige farger vi kan lage på denne måten!).
Ekstra snacks: For de av dere som kan litt binære tall, så ser dere at vi kan skrive 256 ulike tall i to-tallsystemet (0, 1) dersom vi bruker 8 tall (f.eks \(000000000_2=0_{10}\), \(00000001_2 = 1_{10}\), \(00000010_2 = 2_{10}\), ..., \(10011010_2 = 154_{10}\), ..., og \(11111111_2=255_{10}\)), altså \(2^8\) ulike kombinasjoner, som betyr 8-bits tall. Siden fargeverdiene går fra 0-255 uten negative fortegn eller desimaler er det akkurat 256 tall, og vi kan representere fargedata med uint8 (unsigned integer 8-bits) som kan bli nyttig senere når vi jobber med bilder. Dersom vi gjør det sparer vi mye lagringsplass i forhold til dersom vi skulle representert fargeverdiene som float64, dvs. 64-bits flyttall, som ville vært unødvendig siden vi ikke trenger så mye plass til å lagre disse tallene.
Hvordan sammenlikner man bilder?
Det finnes mange metoder for å sammenlikne bilder, men vi har tenkt til å bruke en metode som benytter seg av bildene vi allerede har tatt, og som vi har vært litt borti før her på bloggen da vi skulle se på Radiell hastighetskurve. Vi skal bruke noe som kalles minste kvadraters metode, som er en metode som skal gi oss den beste sannsynligheten for at bildet vi bruker til å sammenlikne med er det riktige bildet. Vi kan utlede metoden fra statistikk, og dermed se at minste verdi i minste kvadraters metode skal gi best sannsynlighet. Jeg skal ikke utlede den her, men ideen eller essensen bak minste kvadraters metode er at dersom vi ikke kan finne en eksakt løsning for det vi er ute etter med dataen vi har, skal vi finne det settet med data som minimerer feilen vi har.
Våre bilder fra verdensrommet
Ideen i vårt tilfelle er at vi skal se hvor like fargeverdiene mellom bildene er, altså ser vi på hvor like RGB-verdier hver piksel i bildene vi sammenlikner er. Dermed bruker vi minste kvadraters metode på RGB-verdiene i hver piksel. Så gjør vi noe lurt: vi legger sammen minste kvadrater av hver piksel i gridet og tar et gjennomsnitt. På denne måten maksimerer vi først sjansen for at RGB-verdien i hver piksel mellom bildene stemmer, også får vi ett tall som representerer likheten gjennom hele bildet. Dette gjør vi for hvert eneste bilde av de 360 bildene vi genererte fra forrige innlegg, også finner vi hvilken grad \(\phi_0\) bildet er sentrert rundt, slik at vi vet hvilken retning bildet er tatt i. Siden vi genererte et bilde for hver grad \(\phi_0 = 0^\circ, 1^\circ,2^\circ,\dots,359^\circ\) kan vi laste dem inn i en array i rekkefølge, og dermed vil indeksen i arrayen også fortelle oss hvilken grad \(\phi_0\) bildet er blitt tatt i. Gjør vi det på denne måten har vi også mulighet til å gjennomføre minste kvadraters metode på alle bildene samtidig, og trenger dermed kun å gjøre det én gang.
For å bruke analogien om arrays fra Rakettmotor - boks for boks om array som en slags skuff/arkivskap med inndelinger, kan vi tenke oss at vi i stedet for med våre pinglete, enkle, veike menneske-armer plukker ut én og én ting fra arkivskapet, bruker Numpy en slags superblekksprut med 360 armer til å plukke ut bildedataen fra skuffen samtidig (eller i løpet av superkort tid: i programmeringslingo kaller vi det vektorisering), og kjøre minste kvadrater for oss for og så pent legge det tilbake igjen pent strukturert. På denne måten kan programmet vi skal lage kjøre fortere enn dersom vi måtte kjørt minste kvadraters metode 360 ganger. Merk at på grunn av inndelingen \(\phi_0\) har vi begrenset med vinkeloppløsning, og svaret vi får er kun en approksimasjon, og ikke nødvendigvis en eksakt løsning.
Minste kvadraters metode for bilder kan skrives som:
\(\begin{align*} \Delta = \sum_{i}^3(P_{i} - P_{ref,i})^2 \end{align*}\)
der \(P\) er en piksel i bildet vi har tatt, \(P_{ref}\) er en piksel i et av referansebildene vi fikk fra forrige innlegg, og summasjonsindeksen er over RGB-verdiene, dvs. at \(i = 1,2,3\)hvor f.eks \(P_1\) da svarer til R-verdien og \(P_3\) svarer til B-verdien i den ene pikselen vi måler i bildet vi skal finne beste approksimasjon til. Vi kan tenke på det som et slags avvik mellom to verdier, som vi kvadrerer slik at det blir positivt (og noen flere grunner). Det ville vært dumt om verdiene nullet hverandre ut, ta dette eksempelet: Vi måler fra et punkt som konstant er 0 og ut til to målinger som er på 4, og -4. Summerer vi differansen uten kvadrater får vi \(\Delta = 4 - 0 - 4 - 0 = 0\). Vi har også to andre målinger på 1 og 2, som vil summere til vil vi få \(\Delta = 2 - 0 + 1 - 0 = 3\). Men målingene på 1 og 2 er jo nærmere 0 enn målingene på 4 og -4? Dermed blir ikke dette et riktig bilde. Kvadrerer vi inne i summen ville vi fått \(\Delta = (4 - 0)^2 + (-4 - 0)^2 = 16+16=32\), og \(\Delta = (2-0)^2 + (1-0)^2 = 4 + 1 = 5\) i stedet, som gir et riktigere bilde av målingene. Da ville også kun målinger tatt i 0 og 0 gitt \(\Delta = 0\).
Dersom vi skal ha et gjennomsnitt av \(\Delta \) i alle pikslene i bildet, må vi summere opp minste kvadrater på hver piksel over hele gridet og dele på størrelsen til bildet. Formelen for å gjøre dette blir da:
\(\begin{align} \overline{\Delta} = \frac{\sum\limits_{i}^X\sum\limits_{j}^Y\sum\limits_{k}^3(P_{k} - P_{ref,k})_{ij}^2}{X\cdot Y} \end{align}\hspace{1cm}(1)\)
der \(X\) er antall piksler i "x-retning" av bildet og \(Y\) er antall piksler i "y-retning" av bildet. Dermed blir \(X\cdot Y\) størrelsen til bildet, altså totalt antall piksler. I våre bilder husker vi fra forrige innlegg at vi hadde bildestørrelser på 640 x 480, dvs. \(X = 640\) og \(Y=480\). Vi kan oppsummere hva vi har tenkt så langt:
- Vi laster inn alle 360 referansebilder vi tok i forrige innlegg, og laster dem inn i en array i rekkefølge fra 0-359. Arrayen vil da inneholde alle RGB-verdiene til hver piksel til alle 360 bilder.
- Vi laster inn bildet vi ønsker å approksimere mest sannsynlige \(\phi_0\) bildet er sentrert rundt.
- Vi bruker minste kvadraters metode på RGB-verdiene mellom referansebildene og bildet vi lastet inn. Dermed finner vi snittverdien av det minste kvadratet for hele bildet, og dette gjør vi for alle 360 bildene ved hjelp av likning (1).
- Vi finner det bildet som hadde minste snitt \(\overline{\Delta}\), og hvilken indeks den hadde i arrayen med alle referansebildene. Siden vi var lure sist og delte inn i grader \(\phi_0=0^\circ,1^\circ,\dots 359^\circ\) vil indeksen i arrayen også været graden \(\phi_0\) bildet ble tatt i (approksimert), og dermed har vi svaret vi ønsker.
Med dette i tankene skriver vi et program som gjør nettopp dette, og vi er klare til å kjøre en test og avduke hvilke resultater vi får!
Bildeavduking, resultater og diskusjon
Fra forrige innlegg husker jeg at jeg sa meg fornøyd med at bildet fra satellitten og referansebildet vi genererte ser like ut. Jeg løy. Det er ikke tilfredsstillende i det hele tatt, og ikke helt vitenskapelig heller. Dermed benytter jeg første muligheten her nå til å teste programmet på bildet vi samplet fra satellitten og bildet vi genererte. Forhåpentligvis får vi et resultat som sier \(\overline{\Delta} = 0\), med tanke på at begge bildene skal være sentrert om samme vinkel \(\phi_0=0\). Vi ruller film, og plotter noen resultater:
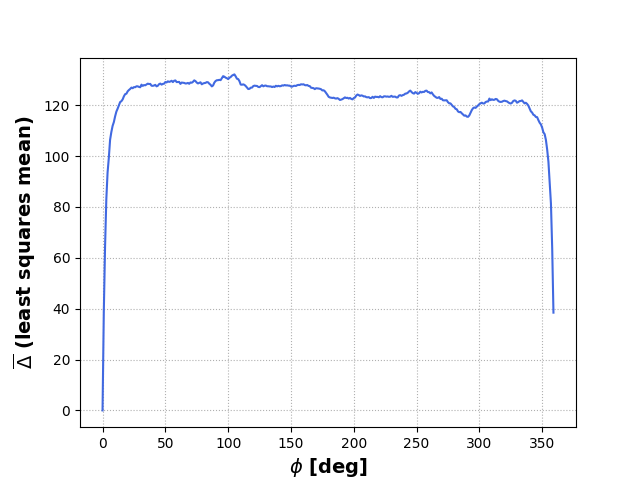
Dette plottet ser bra ut. Vi vet at bildet fra satellitten ble tatt på \(\phi_0=0\), og verdiene fra plottet sier at \(\overline{\Delta}=0\) der \(\phi_0=0\), som betyr at alle RGB-verdiene i begge bildene er like når vi bruker referansebildet sentrert om \(\phi_0=0\). Vi får også returnert at bildet fra satellitten ble tatt med \(\phi_0=0\), som vi tross alt allerede vet, men likevel kjekt å se at den verdien kommer ut (ville vært bekymret om noe annet kom ut). I tillegg ser vi at \(\Delta \) dupper av mot slutten der \(\phi_0\) nærmer seg \(359^\circ\), som gir mening siden vi nesten er tilbake til \(\phi_0=0^\circ\). Dette vil jo skje med alle bilder som er sentrert på en \(\phi_0=0^\circ,1^\circ,\dots,359^\circ\), fordi vi har referansebilder som er generert med nøyaktig disse verdiene. Vi prøver å generere et bilde til på en desimal vinkel som ikke allerede finnes i arrayen med referansebilder, så la oss prøve å generere et bilde som er sentrert om en vinkel \(\phi_0 = 323.67^\circ\). Vi kjører dette inn i koden vår, og får dette plottet:
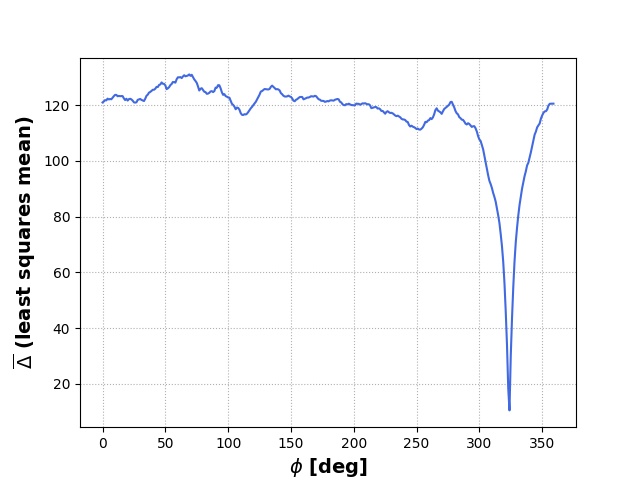
Dette plottet ser også greit ut, og verdiene vi får returnert er \(\overline{\Delta} = 10.47\) og \(\phi_0 = 324^\circ\), som er nærmeste hele grad til \(\phi_0 = 323.67^\circ\), altså en grei approksimasjon. Vi legger også merke til at \(\overline{\Delta}\) minker når vi nærmer oss riktig verdi, som gir mening med tanke på at bildet blir likere og likere rundt beste approksimasjon. Slik kunne vi hold på med evig mange \(\phi_0\) (og det har jeg da programmet kjørte for første gang), men jeg sier det er nok med testing av ulike \(\phi_0\) i dette innlegget (for nå). I stedet ønsker jeg å vise litt mer visuelt hva som skjer her når vi bruker minste kvadrater.
En litt mer visuell fremstilling
Vi kan prøve å visualisere på noen andre måter også. La oss bruke \(\phi_0 = 234.8^\circ\). Vi får fra programmet at \(\overline{\Delta} = 3.27\) og \(\phi_0 = 235^\circ\), slik at det er på plass. Bildet vi har generert ser slik ut:
med et \(\overline{\Delta}\)-plot som ser slik ut:
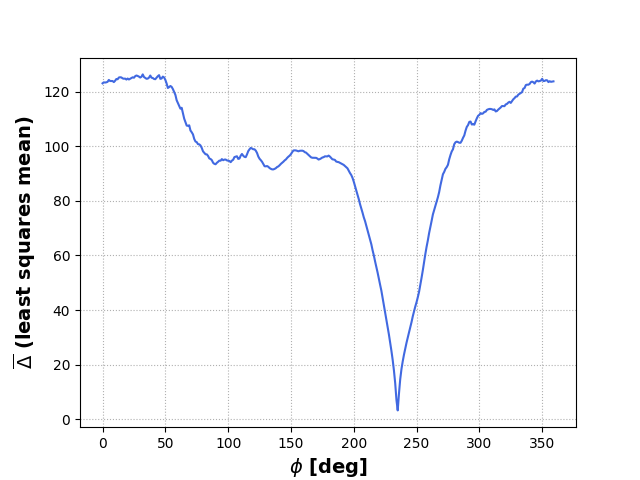
Veldig greit. Det vi derimot kan lese av er at den største verdien for \(\overline{\Delta}\) er på \(\phi_0 = 32^\circ\)(jeg zoomet skikkelig langt inn på plottet lzzm). Hvordan ser forskjellen mellom verste og beste approksimasjon ut når vi regner er? Hvis jeg bare viser deg hvordan bildene der vi har brukt minste kvadraters metode på hver piksel, ser man kanskje bedre hva som er forskjellen mellom en god og en dårlig tilnærming.
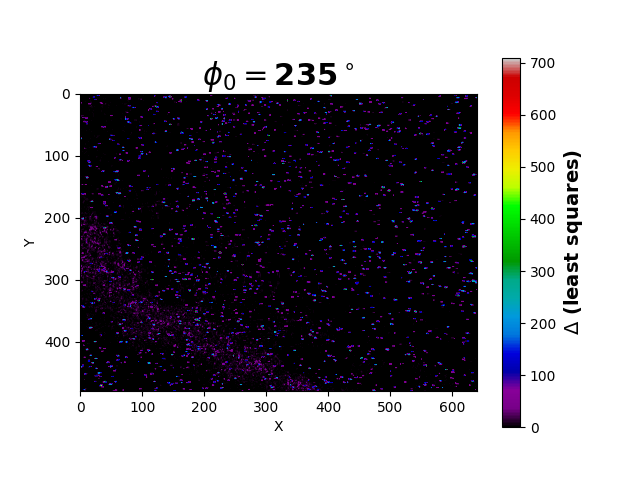
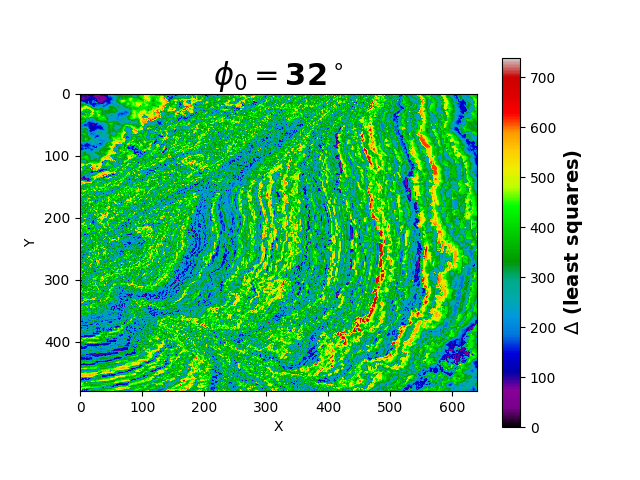
Siden vi tar en forskjell i verdien på RGB og kvadrerer det, betyr det at lave verdier er piksler der RGB har vært like på alle tre. For eksempel \(\sum[(122, 225, 81) - (120, 231, 79)]^2 = \sum(2, -6, 2)^2 = \sum(4,36,4) = 44\), som ville slått ut som lilla på plottene i figur 4 og figur 5. Høye verdier tilsvarer veldig ulikt på alle tre RGB-verdier, og på midten kan det være noen som trekker de andre opp/ned etc.
Litt diskusjon på tampen - forrige innlegg og dette innlegget
I dette innlegget har vi ikke gjort mange antakelser eller approksimasjoner, men det er like vel noen ting vi kan snakke om. Det første vi kan snakke om er vinkeloppløsningen på referansebildene, som begrenser hvor nøyaktige vinkler vi kan finne. Med måten vi har gjort det på får vi opp til nærmeste grad, som betyr at største avviket vi kan ha fra en vinkel er \(0.5^\circ\). Dersom vi skal reise 1AU (snittavstanden mellom sola og jorda når jorda har gjort et omløp rundt sola, 1AU=149598073km) med en vinkelfeil på \(0.5^\circ\)kan vi med enkel trigonometri sette opp en likebent trekant og bruke cossinus-setningen (\(a^2 = b^2 + c^2 - 2bc\cos(A)\), der \(A\) er vinkelen på motsatt side av lengden \(a\)), og finne ut at vi har havnet en avstand \(\sqrt{2\cdot(149598073\text{km})^2 - 2\cdot(149598073\text{km})^2\cdot\cos(0.5^\circ)} \approx 1\;305\;485\text{km}\) unna den opprinnelige kursen, som betyr at vi er skikkelig på avveie. Dette kan man minimere ved å ha flere målinger med mindre vinkel mellom. For eksempel kan vi måle hver \(0.1^\circ\) slik at vinkelavviket er maksimalt \(0.05^\circ\), som betyr at vi må ta 10x antall bilder, men vi vil også bare få ca. \(\frac{1}{10}\) av lengden feil, dvs. ca \(130\;548\text{km}\).
I tillegg gjorde vi en antakelse i forrige innlegg: himmelbildet er konstant. Det er bare tilnærmet sant dersom vi gjør dette i en kort nok tidsperiode. Dersom vi hadde tatt referansebildene og så ventet en laaang tid, ville jo himmelbildet faktisk ha endret seg, og vi kunne ikke brukt referansebildene til å gjøre denne analysen. Vi måtte altså ha hentet ny data, slik at vi kunne sammenlikne igjen. Dette blir ikke noe problem for oss.
En annen ting vi også bør passe på er antakelsen om vi kan bruke minste kvadraters metode. Det går som regel greit, men det er et par forutsetninger med den som vi ikke har gått gjennom her som fort kunne gjort at vi får merkelige resultater.
En siste måling - meningen bak alt våset jeg nå har rablet og bablet om
Som avslutning på det hele skal jeg gjøre det vi nettopp egentlig kom hit for: vi skal finne ut hvilken retning vi faktisk peker! *snufs* blir emosjonell av å tenke på at dette innlegget snart er slutt. Vi bruker romsonden på raketten vår og genererer et siste bilde, og resultatet blir følgende:
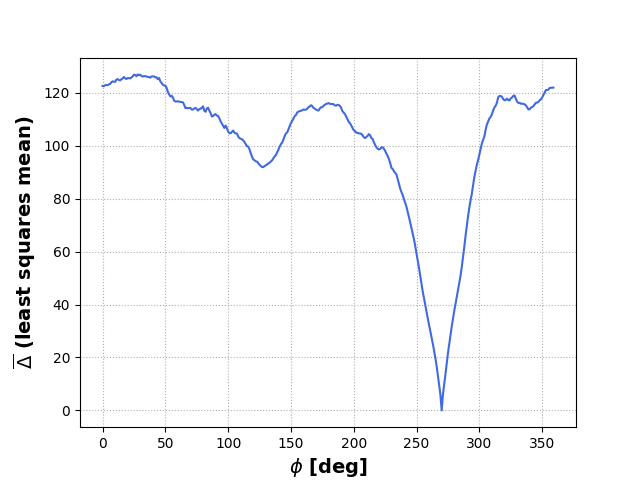programmet spytter ut en \(\phi_0 = 270^\circ\)og en \(\overline{\Delta} = 0\), så ganske nøyaktig \(\phi_0=270^\circ\) med andre ord! Jeg sender dette resultatet videre med dere til Johan, som skal gjøre noe helt annet!