Kilde: thequantumtunnel.com
La oss starte med å friske opp i hva dopplereffekten er for noe. Vi har formelen
\(\begin{align} \frac{\Delta\lambda}{\lambda_0}=\frac{v_r}{c} \end{align}\),
hvor \(\lambda_0\) er bølgelengden slik bølgen blir sendt ut fra et legeme, \(\Delta\lambda=\lambda-\lambda_0\), hvor \(\lambda\) er den målte bølgelengden mottatt fra et legeme, \(v_r\) er en radielle hastighetskomponenten de to legemene beveger seg med relativt til hverandre og \(c\) er gode, gamle lysfarten. Ta gjerne en titt på innlegget om radiell hastighetskurve hvor dette fenomenet blir beskrevet litt grundigere.
Så, hva er motivasjonen vår for å komme drassende med denne effekten nok en gang? Tenk nå på følgende situasjon. Du får en tegning av en kule, med et aksekors i sentrum av kula.
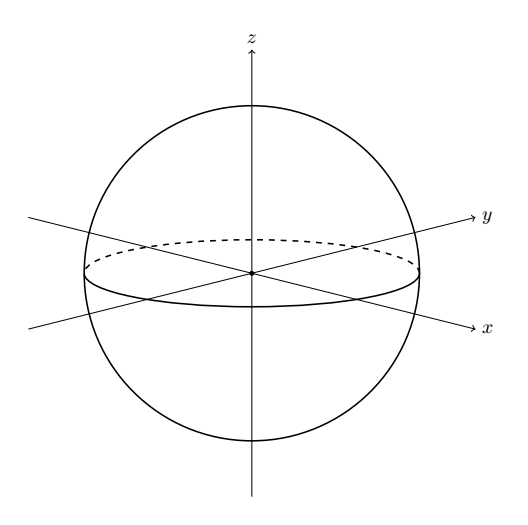
Hvis du nå hadde fått beskjed om å peke på Figur 1 og si hvilken vei som er "opp", så hadde du kanskje pekt over z-aksen. Forestill deg nå at Figur 1 illustrerer jordkloden, og at polene ligger på z-aksen. Hva tror du en forsker som befinner seg på sydpolen vil kalle "opp"?
Ettersom at vi definerer solsystemets origo i sentrum av stjerna vår, så trenger vi å kunne beskrive hastigheten og retningen vår i forhold til stjerna. Det første vi trenger er to referansestjerner. Vi har med oss noen målinger som forskere ved IPA (Interplanetary Aeronautics, vårt svar på NASA) har gjort. De viser bølgelengder av \(H_{\alpha}\)-spektrallinjer (en spesiell emisjonslinje for hydrogen), fra to stjerner ved vår hjemstjerne. Ikke spør oss hvordan de har fått til det, men våre egne beregninger bekrefter at dette stemmer. Vi vet at bølgelengden til \(H_{\alpha}\) i et inertialsystem (ikke-akselerert system) er \(656.3\) nanometer (nm), som heretter vil være vår \(\lambda_0\).
Det første vi trenger er en formel som sier hva radiell hastighet er, ved en gitt bølgelengdeforskyvning. Det er enkelt, vi manipulerer formelen over, og får
\(v_r=\frac{c\Delta\lambda}{\lambda_0}\)
Vi har fått målingene av forskyvningen fra IPA-forskerne, som gir referansestjerne 1 og 2 henholdsvis \(\Delta\lambda_1=-0.016\,nm\) og \(\Delta\lambda_2=-0.015\,nm\). Negative tall her betyr at bølgelengden de har mottatt er kortere, altså må stjernene bevege seg mot oss. Vi ønsker å finne vår hjemstjernes radielle hastigheter relativt til referansestjernene. Vi snur retningen, og får
\(v_{r,1}=1.59\,AU\\ v_{r,2}=1.46\, AU\)
Kan dere tenkte dere hvilken hastighet romskipet vårt hadde hatt, dersom vi målte \(\Delta\lambda=0\) for begge referansestjernene? Den måtte blitt det samme, måtte den ikke? For det hadde betydd at vi beveget oss med samme radielle hastighet som referansestjernene!
Nå må vi ta en titt på hvordan dette vil se ut. Vi definerer positiv radiell hastighet som at stjerna vår beveger seg en eller annen retning. Forskerne ved IPA har også gitt oss vinklene til de to referansestjernene i forhold til vårt xy-system. De er \(\phi_1=320.6^\circ\,,\,\phi_2=201.3^\circ\). Det ser altså slik ut:
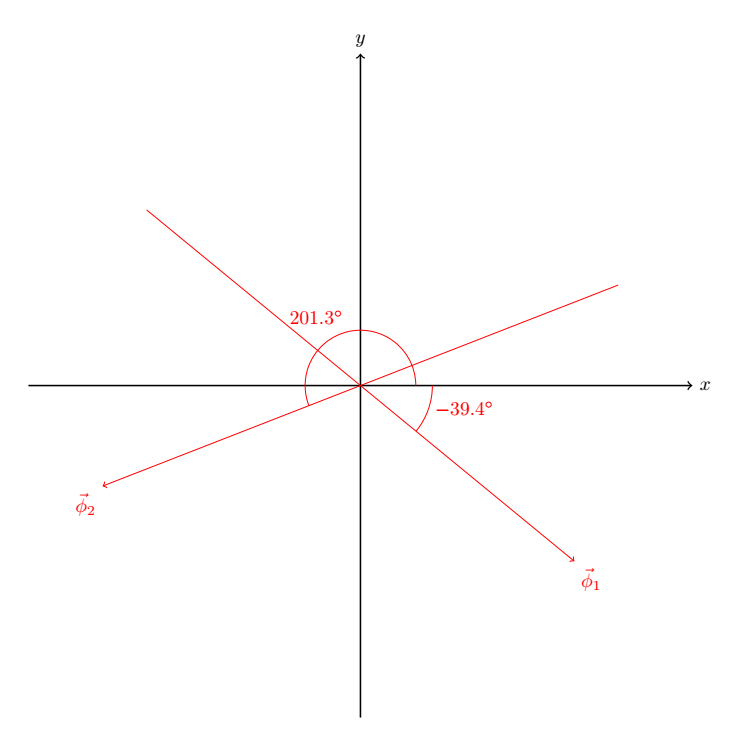
Når vi nå legger inn de radielle hastighetene i \(\phi\)-systemet, ser det slik ut:

Dette viser hvilken størrelse og retning det er på hastigheten til sola vår, relativt til referansestjernene. Men hvordan kan vi uttrykke dette i vårt kjente xy-system? Vi trenger å gjøre en koordinattransformasjon. Vi har en matrise som kan løse dette for oss:
\(\begin{align*} \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sin{(\phi_2-\phi_1)}} \begin{bmatrix} \sin{\phi_2} & -\sin{\phi_1}\\ -\cos{\phi_2} & \cos{\phi_1} \end{bmatrix} \begin{bmatrix} p_1\\p_2 \end{bmatrix} \end{align*}\)
Her er \(p_1\,,\,p_2\) koordinater i \(\phi\)-koordinatsystemet, med sine respektive vinkler \(\phi_1\,,\,\phi_2\). Hvis vi gjør denne transformasjonen for \(v_{r,1}\,,\,v_{r,2}\) over, får vi
\((x,y)=(0.40,2.99)\,AU/yr\)
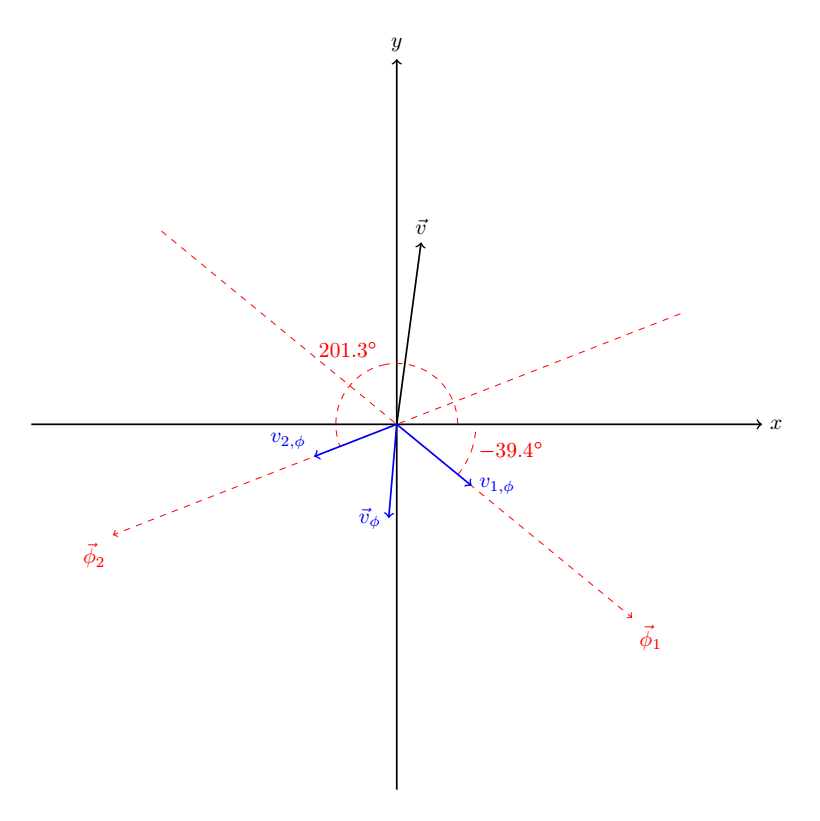
Dette er altså hastigheten hjemsterna vår beveger seg med i xy-systemet. Det kan se litt rart ut, at stjerna vår først beveger seg i negativ x- og y-retning, og så i positive retninger. Dette handler om hvordan vi definerer vårt xy-system. Det koordinattransformasjonen gjør er på en måte å "vri" aksene til \(\phi\)-systemet slik at de ligger oppå x- og y-aksen.
Grunnen til at vi gjør det på denne måten er at dersom vi nå måler en bølgelengdeforskyvning fra de to stjernene, om bord på romskipet vårt, kan vi transformere dem til xy-systemet og finne vår hastighet relativt til vår hjemstjerne. Når vi nå skal finne romskipet hastighet i xy-systemet, kan vi transformere hastigheten fra \(\phi\)-systemet, og trekke fra hastigheten til stjerna vår. Da kan vi alltid vite hvor vi er på vei, i forhold til vår hjemstjerne. Det er ganske kult, er det ikke?
Her er en liten test på at metoden vår fungerer: La oss si at vi måler en forskyvning om bord i romskipet vårt, som er det samme som målingene vi fikk fra IPA (sett \(\Delta\lambda_1=-0.016\,nm\) og \(\Delta\lambda_2=-0.015\,nm\)). Da beveger vi oss med samme radielle hastighet mot de to referansestjernene som stjerna vår, så den relative hastigheten mellom romskipet vårt og stjerna skal bli 0. Og det blir den. Prøv gjerne selv.
Nå som vi vet at metoden funker, skal vi faktisk måle forskyvningen fra de to referansestjernene. Romskipet vårt er utstyrt med teknologi som klarer dette. Vi får
\(\Delta\lambda_1=0.037\,nm\\ \Delta\lambda_2=0.016\,nm\)
Dette betyr at stjernene er på vei bort fra oss. Vi bruker disse forskyvningene, og regner ut vår relative hastighet i xy-systemet. Deretter må vi trekke fra hastigheten stjerna har, og vi står igjen med
\(\vec{v}=(0,8.124)\,AU/yr\)
Det er en voldsom hastighet, på nesten \(140\,000\,km/t\). Det er godt vi har sikkerhetsbelte på.
Forrige innlegg << Neste innlegg >>
