Vi har altså avstandene fra romskipet vårt til alle planetene og stjerna i solsystemet vårt. Det vi skal gjøre nå er å bruke disse avstandene til å finne ut nøyaktig hvor vi er i forhold til et punkt. Vi starter med avstanden \(r_1\) til stjerna vår, som ligger i origo. Er dere da enige i at vi må befinne oss på sirkelen rundt origo med radius \(r_1\)?

Ettersom at vi vet at vi befinner oss en avstand \(r_1\) fra stjerna vår, vet vi altså at posisjonen vår må være et eller annet sted på sirkelen i Figur 1. Videre kan vi bruke avstanden \(r_2\) fra hjemplaneten vår til å finne den sirkelen vi må befinne oss på i forhold til den. Nå kommer poenget: Disse to sirklene vil skjære hverandre på minst ett sted. Ser du hvorfor?

Nå ser dere kanskje hva som skal til for å snevre inn posisjonen vår til bare ett punkt? Helt riktig, vi trenger en tredje sirkel.
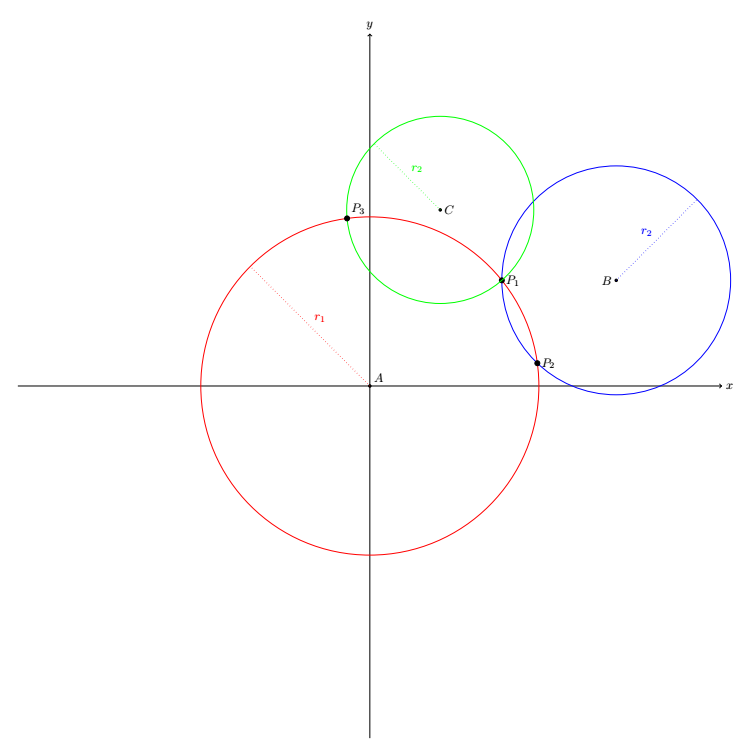
På Figur 3 ser dere at de tre sirklene har ett felles skjæringspunkt \(P_1\). Det betyr at vi må befinne oss her. Hvorfor er det sånn? Jo, husk at formelen for en sirkel med sentrum i \((x_1,y_1)\) og radius \(r\) er gitt ved
\((x-x_1)^2+(y-y_1)^2=r^2\)
Dette er en likning som gir oss alle punktene \((x,y)\) som er en avstand \(r\) fra sentrum \((x_1,y_1)\). Ser dere hvorfor? Hint: Bruk Pythagoras' læresetning.
Nå skal vi finne et generelt utrykk for hvor vi befinner oss ved bruk av denne metoden. Hvis du ikke er veldig interessert i matematiske utledinger, kan du hoppe ned til der du ser denne linjen: -------------------------------------
Vi starter med tre generelle likninger for tre sirkler.
\(\begin{align} \text{I}:\quad (x-x_1)^2+(y-y_1)^2&=r_1^2\\ \text{II}:\quad (x-x_2)^2+(y-y_2)^2&=r_2^2\\ \text{III}:\quad (x-x_3)^2+(y-y_3)^2&=r_3^2 \end{align}\)
Vi utvider likningene:
\(\begin{align} \text{IV}:\quad x^2-2xx_1+x_1^2+y^2-2yy_1+y_1^2&=r_1^2\\ \text{V}:\quad x^2-2xx_2+x_2^2+y^2-2yy_2+y_2^2&=r_2^2\\ \text{VI}:\quad x^2-2xx_3+x_3^2+y^2-2yy_3+y_3^2&=r_3^2 \end{align}\)
Vi trekker likning \(\text{V}\) fra likning \(\text{IV}\) og likning \(\text{VI}\) fra likning \(\text{V}\), og samler koeffisientene foran \(x\) og \(y\):
\(\begin{align} \text{IV}-\text{V}:\quad &-2xx_1+2xx_2+x_1^2-x_2^2-2yy_1+2yy_2+y_1^2-y_2^2=r_1^2-r_2^2\\ &=\underbrace{-2(x_1-x_2)}_\text{A}x\underbrace{-2(y_1-y_2)}_\text{B}y=\underbrace{r_1^2-r_2^2-x_1^2+x_2^2-y_1^2+y_2^2}_\text{C}\\ \text{IV}-\text{VI}:\quad &-2xx_1+2xx_3+x_1^2-x_3^2-2yy_1+2yy_3+y_1^2-y_3^2=r_1^2-r_3^2\\ &=\underbrace{-2(x_1-x_3)}_\text{D}x\underbrace{-2(y_1-y_3)}_\text{E}y=\underbrace{r_1^2-r_3^2-x_1^2+x_3^2-y_1^2+y_3^2}_\text{F} \end{align}\)
Vi får nå to nye likninger:
\(\begin{align} \text{VII}:\quad \text{A}x+\text{B}y=\text{C}\\ \text{VIII}:\quad \text{D}x+\text{E}y=\text{F} \end{align}\)
Vi vet at disse to likningene skal gi et entydig svar, som da blir posisjonen til romskipet vårt. Vi løser likning \(\text{VII}\) med hensyn på \(x\), og setter det uttrykket inn i likning \(\text{VIII}\):
\(\begin{align} \text{A}x+\text{B}y=\text{C}\quad\Rightarrow\quad &x=\frac{\text{C}-\text{B}y}{\text{A}}\\ \text{D}x+\text{E}y=\text{F}\quad\Rightarrow\quad&\text{D}\bigg(\frac{\text{C}-\text{B}y}{\text{A}}\bigg)+\text{E}y=\text{F}\\ &\frac{\text{CD}}{\text{A}}-\frac{\text{BD}y}{\text{A}}+\text{E}y=\text{F}\\ &\bigg(\text{E}-\frac{\text{BD}}{\text{A}}\bigg)y=\text{F}-\frac{\text{CD}}{\text{A}}\\ &y=\frac{\text{F}-\frac{\text{CD}}{\text{A}}}{\text{E}-\frac{\text{BD}}{\text{A}}}=\frac{\text{AF}-\text{CD}}{\text{AE}-\text{BD}} \end{align}\)
Med dette uttrykket for \(y\) kan vi løse likning \(\text{VIII}\) med hensyn på \(x\) og sette inn for \(y\):
\(\begin{align} \text{D}x+\text{E}y=\text{F}\quad\Rightarrow\quad x&=\frac{\text{F}-\text{E}y}{\text{D}}\\ &=\frac{\text{F}-\text{E}\Big(\frac{\text{AF}-\text{CD}}{\text{AE}-\text{BD}}\Big)}{\text{D}}\\ &=\frac{\text{F}-\Big(\frac{\text{AEF}-\text{CDE}}{\text{AE}-\text{BD}}\Big)}{\text{D}}\\ &=\frac{\frac{\text{F}(\text{AE}-\text{BD})-(\text{AEF}-\text{CDE})}{\text{AE}-\text{BD}}}{\text{D}}\\ &=\frac{\frac{\text{AEF}-\text{BDF}-\text{AEF}+\text{CDE}}{\text{AE}-\text{BD}}}{\text{D}}\\ &=\frac{\text{CDE}-\text{BDF}}{\text{D}(\text{AE}-\text{BD})}\\ &=\frac{\text{CE}-\text{BF}}{\text{AE}-\text{BD}} \end{align}\)
-------------------------------------------------------------------------------------------------------------------
Vi har altså funnet de generelle koordinatene våre ved hjelp av tre sirkellikninger. Husk tilbake til innlegget der vi regnet ut de numeriske banene til planetene i solsystemet. Der er alle posisjonene til alle planetene. Vi kan enkelt bruke dem ved hvilket som helst tidspunkt, sammen med avstandene til planetene, til å finne ut av hvor vi befinner oss i forhold til stjerna vår, eller hvilken som helst planet i solsystemet vårt, egentlig.
Romskipet vårt måler avstandene til stjerna vår, hjemplaneten vår og vår naboplanet. De er henholdsvis
\(d_*=1.859\,AU\\ d_p=1.177\cdot10^{-4}AU\\ d_{np}=3.133\,AU\)
Vi bruker uttrykket for x- og y-posisjonen fra utledinga over, og får
\((x,y)=(1.859,1.177\cdot10^{-4})\,AU\)
Som vi ser, er posisjonen vår i x- og y-retning den samme som avstanden vår fra henholdsvis stjerna vår og planeten vår. Det er ikke så rart, siden vi har satt stjerna vår i origo.