Vi starter med å se på hvilke krefter som kommer til å virke på romskipet vårt når vi befinner oss et gitt sted i rommet. Vi har krafta fra stjerna og fra alle planetene. For enkelhets skyld neglisjerer vi kreftene fra månene i systemet vårt. Som dere kanskje også husker, så er stjerna vår veldig stor i forhold til sola. Krafta fra den vil være voldsomt mye større enn for eksempel en måne fra den ytterste planeten.
Krafta fra stjerna på romskipet vil være
\(\vec{F}_*=-\gamma\frac{mM_*}{r^3}\vec{r}\)
hvor \(\gamma,m,M_*,r\) er hhv. gravitasjonskonstanten, massen til romskipet, massen til stjerna og lengden eller normen til \(\vec{r}\), som igjen er vektoren fra stjerna til romskipet vårt. Minustegnet gjør at retningen blir riktig, altså at krafta trekker oss mot stjerna.
Når det gjelder kreftene fra de andre planetene, starter vi med å se på én planet.
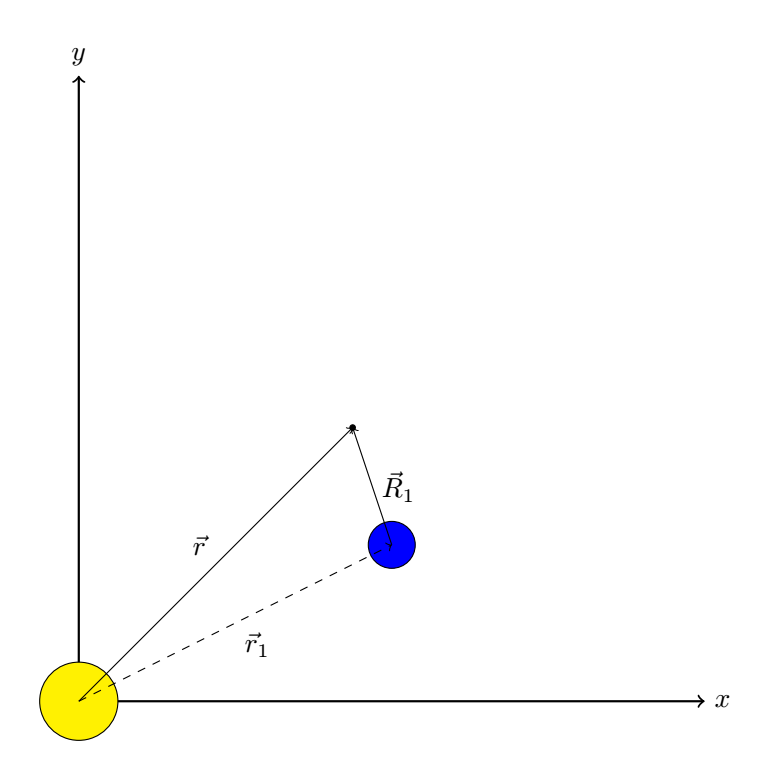
Vi ser at vi kan bruke vektoraddisjon for å finne vektoren \(\vec{R}_1\), som er den vektoren tyngdekraften vil virke langs. Vi får at krafta fra planeten på romskipet blir
\(\vec{F}_1=-\gamma\frac{mM_1}{R_1^3}\vec{R}_1\)
Vi finner et utrykk for \(\vec{R}_1\) slik:
\(\begin{align} \vec{r}&=\vec{r}_1+\vec{R}_1\\ \Rightarrow\vec{R}_1&=\vec{r}-\vec{r}_1 \end{align}\)
For planet nummer 2 blir det tilsvarende.
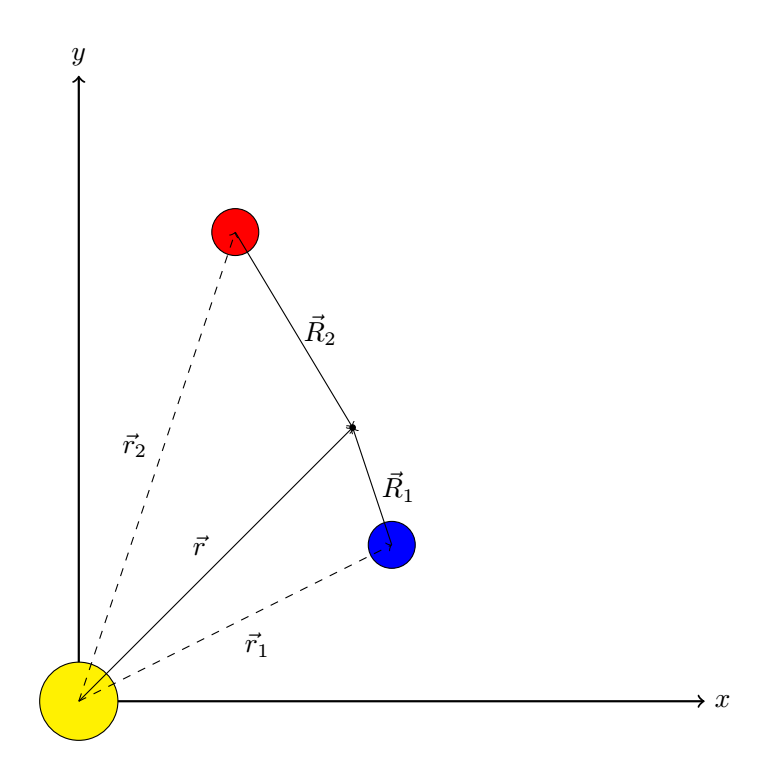
Vi får at krafta fra planet 2 på romskipet blir
\(\vec{F}_2=-\gamma\frac{mM_2}{R_2^3}\vec{R}_2\)
Det vil også virke krefter fra de 6 andre planetene, så vi kan skrive en generell formel for kraftsummen som virker på romskipet fra stjerna og alle de 8 planetene på følgende måte:
\(\begin{align} \vec{F}_\text{tot}=-\gamma\frac{mM_*}{r^3}\vec{r}-\sum_{i=1}^8\frac{\gamma mM_i}{R_i^3}\vec{R}_i \end{align}\)
hvor \(i\) løper over alle planetene, og \(\vec{R}_i=\vec{r}-\vec{r}_i\). Som du kanskje ser, så er dette uttrykket kraftsummen, som betyr at dette må være lik massen til romskipet ganger akselerasjonen. Vi får, for akselerasjonen:
\(\begin{align} \vec{F}_\text{tot}&=m\vec{a}\\ \vec{a}&=\frac{\vec{F}_\text{tot}}{m}\\ &=-\gamma\frac{M_*}{r^3}\vec{r}-\sum_{i=1}^8\frac{\gamma M_i}{R_i^3}\vec{R}_i \end{align}\)
Dette bruker vi til å løse bevegelseslikningene med Euler-Cromer.
Det neste vi må bestemme oss for er når vi vil dra. Altså, når er det gunstig å launche fra planeten vår for å komme fram til destinasjonen vår. Vi ønsker at planetene er så nærme hverandre som mulig, slik at reisetiden blir kortest mulig. Det er egentlig ikke noen spesifikk grunn for at dette er det beste, siden vi kan bruke andre himmellegemer til å slynge oss videre på vår reise. Men, vi kommer til å prøve å finne ut av når planetene er nærmest hverandre.
Husk tilbake til da vi modellerte planetbanene numerisk. Vi kan lete etter den minste avstanden til to av planetene og plotte disse mot hverandre. Det gir dette plottet:
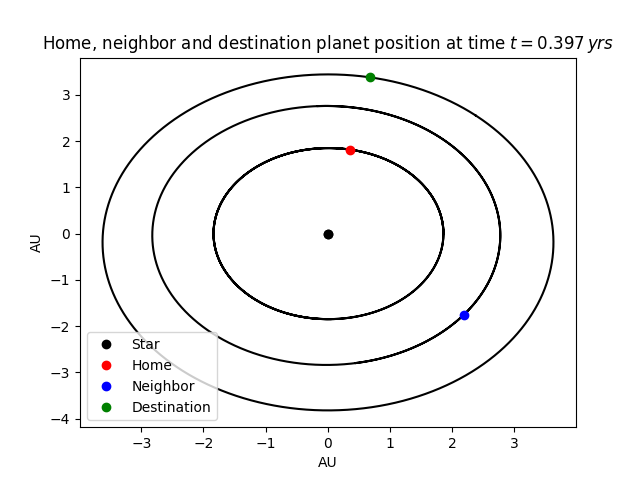
Det vi ønsker å oppnå er å launche fra planeten vår, orientere oss og så sette kursen mot planeten vi skal til. Det eneste som kommer til å bestemme selve banene vår er initialhastigheten vi får med oss fra planetens omløpshastighet. Husker dere eksemplet fra karusellen? Dette er tilsvarende. Systemet sett fra referansesystemet hvor stjerna står i ro og alle planetene beveger seg, gjør at vi kommer til å ha en hastighet og retning lik hastigheten til planeten vår pluss hastigheten vi har når vi har nådd unnslippingshastighet.
Ta en titt på Figur 3. Ser dere at dersom vi skyter opp raketten i x-retning, vil vi motvirke den initialhastigheten vi får med oss fra planeten (anta at planetene beveger seg mot klokka)? Vi vil altså utnytte begge hastighetene så godt som mulig. Vi har prøvd å simulere banen vår på vår datamaskin for å undersøke om vi har gjort riktige beregninger. Dette har vist seg å være vanskelig, så vi har kontakt med forskerne fra IPA som har hjulpet oss med å beregne banene våre, ut fra våre egne parametere.
Vi vet at når avstanden vår fra planeten er
\(l=|\vec{r}|\sqrt{\frac{M_p}{10M_*}}\)
kan vi utføre en orbital injection maneuver (OIM), hvor \(l,\,|\vec{r}|\) er avstanden fra planeten vi skal lande på og avstanden fra stjerna. For å utføre en OIM har vi at
\(\begin{align} (\Delta \vec{v})_{\text{inj}}&=\vec{v}_{\pm}-\vec{v}_0\\ \vec{v}_\pm&=\pm\,\hat{u}_t v_{\text{stable}} \end{align}\)
hvor \(\hat{u}_t\) er enhetsvektor tangentielt på planeten og \(\pm\) angir om romskipet går i bane mot klokken (\(+\)) eller med klokken (\(-\)). Videre er \(\vec{v}_0\) hastigheten romskipet har, og \(v_\text{stable}\) er gitt ved
\(v_\text{stable}=\sqrt{\frac{\gamma M_p}{r}}\)
hvor \(r\) er avstanden fra romskipet til planetens sentrum. Vi har med oss målingsutstyr som gir oss disse størrelsene.
Interpolering
Nå skal vi se på hvordan vi prøvde å få til dette på egenhånd. Da vi regnet ut de numeriske banene, gjorde vi dette med et visst tidssteg (11 000 per år). Dette kan virke bra nok, men vi ønsker å kunne finne en hvilken som helst posisjon til en hvilken som helst tid. Først litt om interpolering.
Store norske leksikon har følgende definisjon av interpolering:
Interpolasjon er i matematikk det å beregne eller anslå verdier av en funksjon mellom verdier som allerede er kjent.
La oss se på et eksempel. Vi har en funksjon \(f(x)=\frac{1}{x}\). Videre har vi datapunktene \(1,2,\dots, 10\). Dette gir oss denne tabellen:
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) | \(10\) |
| \(f(x)\) | \(1\) | \(0.50\) | \(0.33\) | \(0.25\) | \(0.20\) | \(0.17\) | \(0.14\) | \(0.13\) | \(0.11\) | \(0.10\) |
I et plott ser det slik ut:
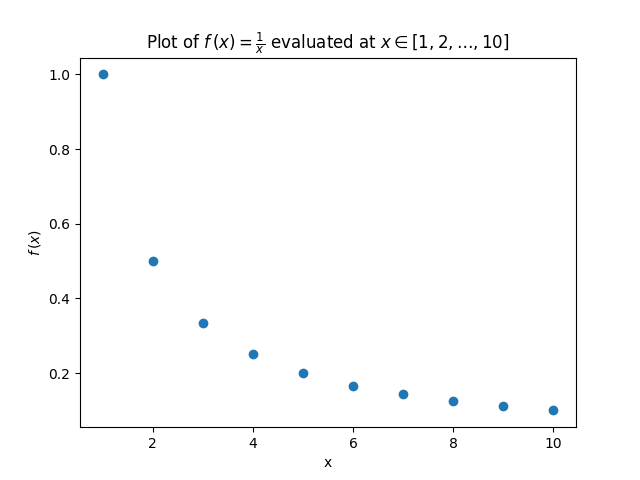
I Figur 4 kan vi se at datapunktene utgjør en slags form. Dette er vel og bra, men vi ønsker større nøyaktighet. Vi kan interpolere funksjonen evaluert i de dataene vi har og med dette øke graden av presisjon. Vi interpolerer lineært, som betyr at vi ønsker å finne den linjen mellom dataintervallet som passer best. Formelen for lineær interpolasjon er gitt ved
\(f(x)\approx f(x_1)+\frac{x-x_1}{x_2-x_1}\Big(f(x_2)-f(x_1)\Big)\)
hvor \(f(x_1),f(x_2)\) er funksjonsverdien for punktene \(x_1,x_2\), for \(x_2>x_1\). Merk dere at dette kan skrives som
\(f(x)\approx f(x_1)+(x-x_1)\frac{\Delta f(x')}{\Delta x'}\)
hvor \(x'\) er funksjonsverdien for de kjente dataene. Ser dere at \(\frac{\Delta f(x')}{\Delta x'}\) blir stigningstallet til den rette linja mellom de to punktene? Vi starter altså med den kjente funksjonsverdien \(f(x_1)\) og legger til differansen mellom det punktet vi har evaluert funksjonen i \(x_1\) og det punktet vi ønsker å evaluere funksjonen i \(x\). Deretter ganger vi denne differansen med stigningstallet til linja mellom de to kjente funksjonsverdiene. Med andre ord lager vi en linje som skal gå fra den første funksjonsverdien til funksjonsverdien av det punktet vi vil evaluere i, med den samme stigningen som den linja fra de to kjente funksjonsverdiene.
Vi hadde det første intervallet vårt \([1,2,\dots,10]\). Vi deler opp slik at det blir 10 nye punkter mellom hvert kjente punkt \([1.01,1.03,\dots,9.09,10]\). Ved å bruke formelen på hvert av disse punktene og trekke en linje mellom hvert punkt, får vi følgende plott:
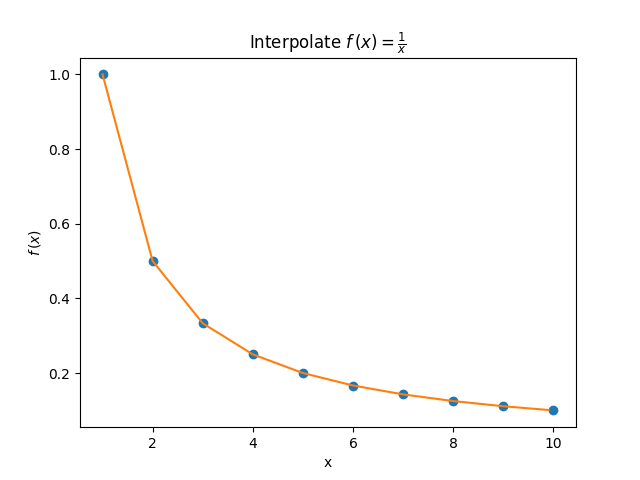
Ettersom at dette er en lineær interpolasjon, får vi rette linjer mellom punktene. Jo flere punkter vi velger mellom hvert kjente datapunkt, jo "smoothere" blir linjen.
Men hva skal vi bruke dette til? Se for dere følgende situasjon: person A sitter i bilen sin og person B sitter på et tog. A skal kjøre over en bro som går over togskinnene og kaste en ball ut av vinduet sitt. På taket av toget er det plassert en veldig stor kurv, som ballen forsøksvis skal treffe. Kurven er plassert direkte over der B sitter. Hvert tiende minutt sender B automatisk sin posisjon til A. A ser hele tiden sin egen posisjon og B sin posisjon som prikker på et kart, men har ikke mulighet til å stanse bilen, kun bremse. Dessuten kan ikke A se eller høre toget på noe tidspunkt. Kan A klare å beregne posisjonen sin i forhold til posisjonen til B med tilstrekkelig presisjon til å klare å treffe kurven på taket av toget?
Ser dere at så lenge A og B er langt unna hverandre, så kan A være trygg på at han ikke er for tidlig eller for sent fremme på broen. Problemet melder seg når de to nærmer seg hverandre. Hvis A får et signal om B sin posisjon 5 minutter før B vil være nøyaktig under broen, vil han få det neste signalet når B er 5 minutter forbi broen. Mellom her kan ikke A si noe om hvor B befinner seg. Han har for få datapunkter!
Det er dette som kan skje når vi prøver å treffe planeten vi skal reise til. Hvis vi leter etter en posisjon som befinner seg mellom to tidssteg må vi gjette på omtrent hvor planeten befinner seg. Husk at vi har formler for både hvilken avstand vi må være fra planeten og hvor langt vi må være unna planetens sentrum for å kunne gjennomføre OIM.
Vi har utført de fleste av beregningene selv, men dessverre får vi ikke riktige resultater. Når vi endrer tidspunktet for launch, klarer vi ikke med stor nok nøyaktighet å beregne hvor vi befinner oss på planetoverflaten. Når vi interpolerer på en datamaskin er det mye som kan gå galt. Dette er et konsept som for oss er veldig enkelt, men det å implementere det på en datamaskin har vist seg å være helt forskjellig fra vår erfaring. Flaks at vi har kompetente folk på vårt lag!
Planen vår er derfor å sende over noen skjemaer til IPA med de verdiene vi ønsker, for så å få dem til å beregne banen for oss slik at vi kommer oss i orbit rundt planeten. I neste innlegg skal vi se litt videre på hvordan vi har tenkt, og det vil bli presentert noen teoretiske muligheter for å komme i orbit.