Verdensrommet er farlig
Endelig er tiden inne for at vi skal reise. Vi har hittil simulert planetbaner, vi har funnet destinasjonsplaneten (reisemålet), funnet ut av hvilken rute vi skal reise i tillegg til at vi har simulert reisen. Da er vel alt klart? Vel, egentlig ikke. Dere ser kanskje illustrasjonen ovenfor? Det er en simulering av hvordan en romreise kunne sett ut. I teorien ser det fantastisk ut, men i virkeligheten finnes det flere kompliserende faktorer. For eksempel kan det finnes små astronomiske legemer som måner som vi ikke har regnet med, eller usikkerheter i planetbanene vi har simulert som fører til at krefter på oss fra planeter og liknende kan avvike litt. I tillegg finnes det ofte også usikkerheter i selve simuleringene som vi gjør, selv uten alle de førnevnte faktorene. Dermed kommer vår simulerte rakett-bane til å avvike litt fra den virkelige banen, faktisk nok til at vi bommer på destinasjonen. Dette er dårlig stemning, så derfor må vi gjøre noen korreksjoner på kursen vår underveis.
Hvordan skal vi korrigere kursen?
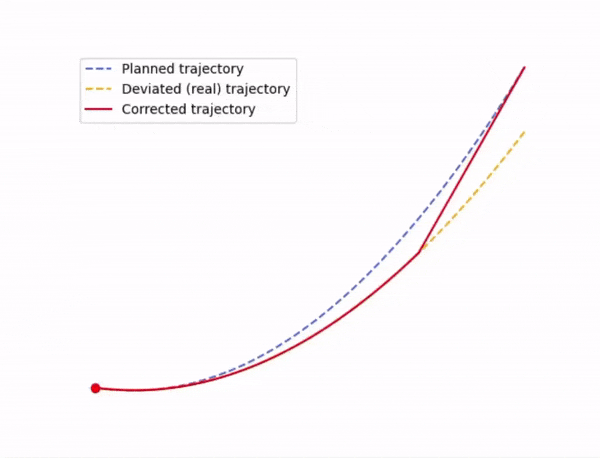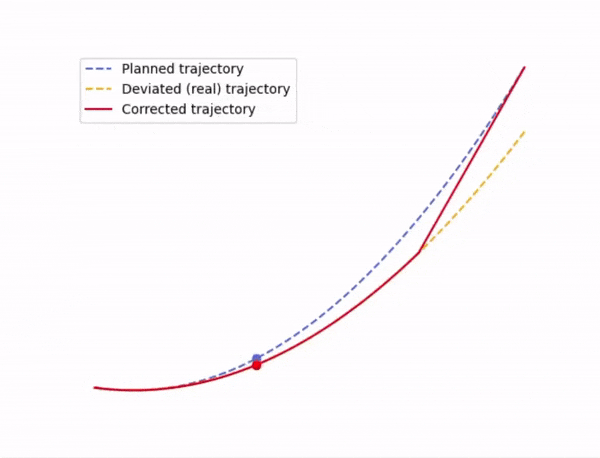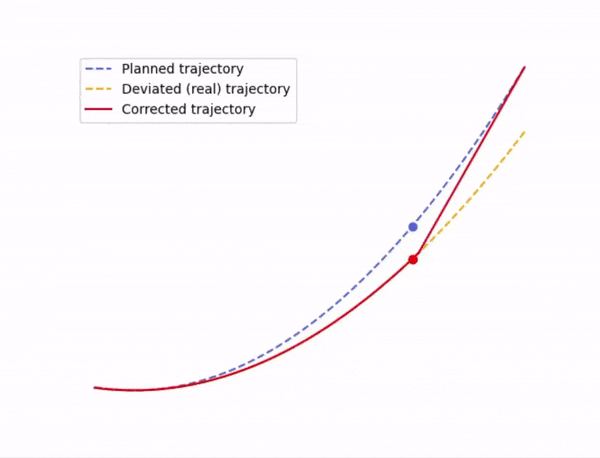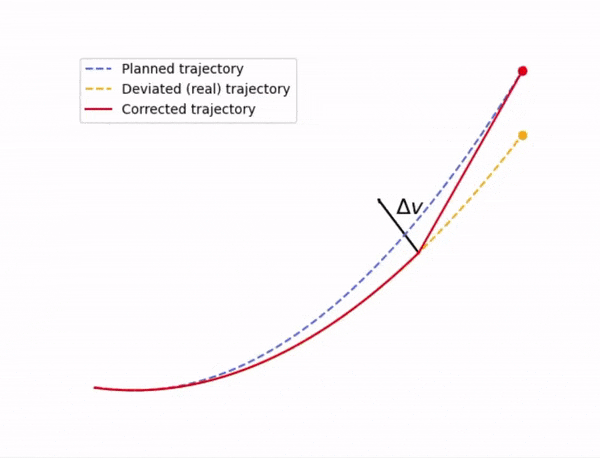
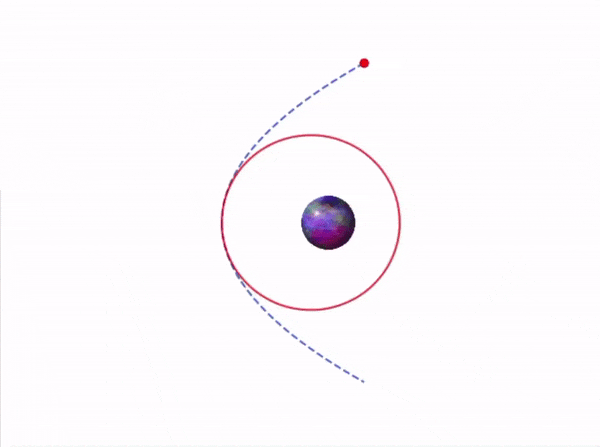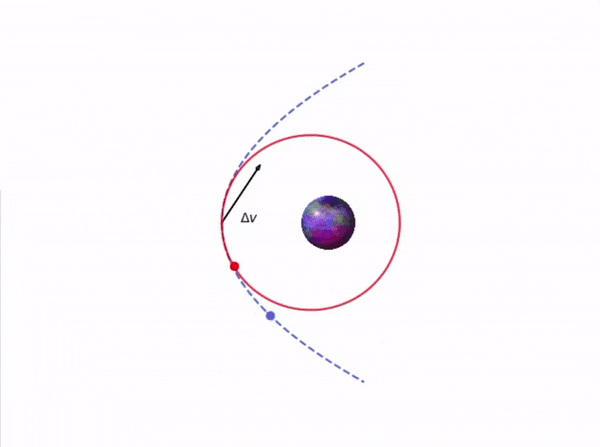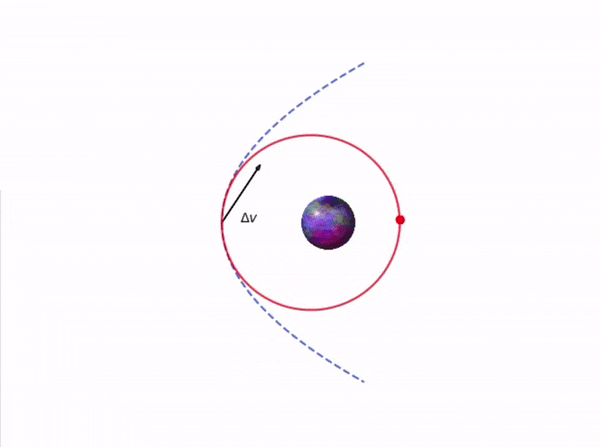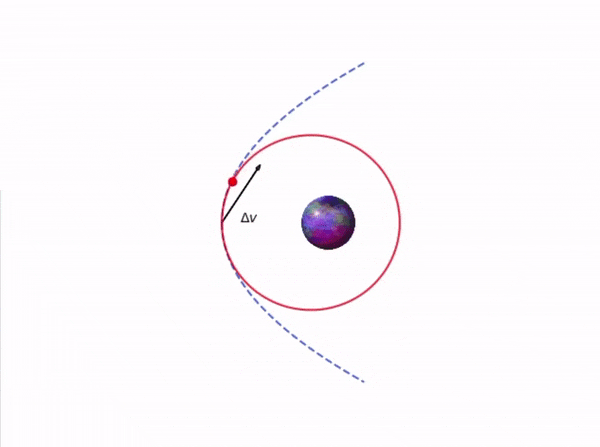
Dette blir ikke store magien. For å korrigere kursen booster vi oss selv med en hastighetsendring \(\Delta \vec{v}\) slik at banen vi er på endrer kurs, likt som på Figur 1 nedenfor. Det eneste vi trenger å passe på her er hvor stor boosten er, når vi ønsker å booste, og at vi gir korreksjonen i riktig retning.
Programmet for å gjøre hele romreisen med boostene har vi fått av en gruppe forskere som utvikler den nyeste teknologien innenfor romreise, sammen med koder for å flyte fritt og orientere oss i den retningen vi ønsker ute i verdensrommet. Ja vi har til og med fått med oss et kamera slik at vi kan ta bilder av omgivelsene rundt oss! Herlig! Dette gjør det enklere for oss å gjennomføre reisen. Jeg kan lukte stjerner og planeter!
Måten vi da vil gjøre dette på er å bruke kameraet på raketten vår til å finne ut hvor vi er i solsystemet til et gitt tidspunkt, slik at vi kan observere hvor vi er dersom (eller når) vi flyter ut av den planlagte kursen. Når vi ser det, kan vi gi oss selv en boost i riktig retning. Vi har heldigvis laget oss en del test-raketter, slik at vi kan teste dette før vi skyter oss selv opp i verdensrommet.
Når vi endelig når planeten vi skal til, kommer vi antakeligvis til å ha så stor hastighet inn mot den at gravitasjonsfeltet ikke klarer å fange oss. Vi ønsker å gi oss selv en boost slik at vi havner i bane rundt planeten.
Illustrasjonen er laget med matplotlib.
Vi starter med å anta at planeten vår og raketten er et 2-legeme-system, for å gjøre dette enklere for oss, selv om det ikke er 100% sant. Dersom du husker fra da vi regnet på ellipsebaner i postene Sol-dans og planet-vals og Planetbaner, så fikk vi at den totale kinetiske energien til et legeme om det andre legemet ble
\(E = \frac{1}{2}\hat{\mu}v^2 - \frac{\hat{\mu}m}{r}\),
der \(\hat{\mu}\) er den reduserte massen \(\hat{\mu} = \frac{m_1m_2}{m_1 + m_2}\), \(m = G(m_1 + m_2)\) og \(m_1,\;m_2\) er massen til de to legemene, og \(v\) er farten til det ene legemet sett fra det andre legemet. Du husker også kanskje at for at vi skal ha en ellipse-bane, måtte denne totale energien også være negativ, altså \(E<0\) ? (Hvis ikke anbefaler jeg deg å skumme gjennom innleggene om ellipsebaner ovenfor en gang til). Dersom \(E\) ikke er mindre enn null, er vi ikke lenger i en ellipsebane om massen i to-legeme systemet, som betyr at vi heller ikke lenger går i bane rundt planeten. Løser vi
\(\)\(\frac{1}{2}\hat{\mu}v^2 - \frac{\hat{\mu}m}{r} < 0\)
får vi at den maksimale hastigheten vi kan ha når vi skal inn i bane er
\(v_{max} = \sqrt{\frac{2G(m_1 + m_2)}{r}}\).
Siden massen til planeten \(m_2\) er mye større enn massen til raketten \(m_1\), kan vi se bort ifra vår egen masse når vi legger \(m_1\) og \(m_2\) sammen (MERK dette kan vi IKKE gjøre når vi ganger massene sammen). Vi får da at vi kan ha en maksfart på
\(v_{max} = \sqrt{\frac{2Gm_2}{r}}\).
Men vi må også passe på å ikke sakke ned for mye slik at vi ikke går i bane lenger, og faktisk faller ned mot planeten. For en elliptisk bane kan vi finne denne minimumsverdien med vis-viva likningen (bit merke i denne).
\(v = \sqrt{Gm_2\left(\frac{2}{r} - \frac{1}{a}\right)}\)
Problemet med denne er at vi trenger nå å vite hva store halvakse i ellipsebanen er før vi har kommet inn i ellipsebanen. Dette gjør det mye vanskeligere for oss, derfor tenker vi oss at vi booster på en slik måte at vi havner i en ellipsebane, som vi kan approksimere til en sirkelbane for å gjøre det enkelt for oss. Resultatet vi får nå blir kun en approksimasjon til et tenkt teoretisk scenario, men gir oss et slags estimat på hvor lav fart vi kan ha. Husk at vi ikke ønsker å havne i en kjempe-elliptisk bane, men en ganske pen nesten-sirkulær bane. Jo roligere og penere banen vår rundt planeten er jo lettere er den å håndtere, slik at vi kan ligge i en stabil bane. Vi bruker at kraften på raketten fra planeten er \(F = m_1a = m_1\frac{v^2}{r} = G\frac{m_1m_2}{r^2}\). Løser vi dette for \(v\) får vi at
\(v_{min} = \sqrt{\frac{Gm_2}{r}}\).
MERK: Dersom vi hadde latt store halvakse \(a=r\) i vis-viva likningen hadde vi fått samme resultat som ovenfor for \(v_{min}\), men måten vi tenkte på her var kanskje litt mer vandt til det dere har gjort på videregående? Merk også at \(a=\infty\) hadde gitt oss uttrykket for \(v_{max}\), så det er tydelig at vi er på riktig spor her.
Dermed får vi at i en avstand \(r\) fra planetens sentrum, har vi to grenser for farten vi kan ha i bane om planeten
\(v_{min} = \sqrt{\frac{Gm_2}{r}}\) og \(v_{max} = \sqrt{\frac{2Gm_2}{r}}\).
Vi har at massen for planeten vi skal reise til er \(m_2 = 1.65\cdot10^{23}kg\) (Jordas masse er \(5.97\cdot10^{24}kg\)), og en radius \(r_p = 1861.74km\) (Jordas radius er på \(6371km\)). La oss si vi skal holde oss 2000km over overflaten, slik at vi ikke roter oss inn i atmosfæren. Da får vi en total avstand \(r = 3861.74km\). Dette gir oss maks og min fart på
\(v_{min} = 1678.43m/s\), \(v_{max} = 2373.66m/s\)
eller
\(v_{min} = 6042.37km/t\), \(v_{max}= 8545.20km/t\).
Dette er kritiske verdier for hvilken fart vi kan ha inn i bane rundt planeten. Disse verdiene er viktige å notere, så vi løper til programmene våre for å skrive det inn så fort som fy!
Zabka-tage
* --------------------------------------------------------------------------------*
*
*
*
*
*
*
*
*
*
* --------------------------------------------------------------------------------*
Er det karatelegenden William Zabka??

Nei, vent, William Zabka hva er det du gjør! Du ødelegger PROGRAMMENE VÅRE! Nei, nei, nei, nei, nei! Hvorfor gjorde du det? Vi prøver i all desperasjon å se om vi kan fikse kodene, om ikke minst bruke dem til noe som helst slik at vi kan komme oss av sted. Det er dessverre til ingen nytte. Vi får absolutt ikke godkjent posisjonen eller orienteringen vår etter launch, så da aner vi jo ikke hvor vi er i verdensrommet når vi skyter oss ut! Hva skal vi gjøre nå?
William Zabka har sabotert oppdraget vårt, den slu, karate-sparkende, romreise-sjalu bølla! Jeg visste vi ikke skulle avslått søknaden hans om å få være med på prosjektet! Nå er vi nødt til å finne en annen måte å komme oss til destinasjons-planeten på. Vi har ikke tid til å fikse programmene, så vi kryper til IPA (International Planetary Association) og forklarer dem det hele. I dyptsynkende medlidenhet designer de en rakett til oss som tar oss med helt til planeten vår, og får raketten i stabil bane om destinasjonsplaneten. Ikke moro.
Ja, dette skulle blitt en skikkelig feiringens innlegg, der vi når vårt endelige reisemål. I stedet blir det en gjensittende følelse av å ikke mestre romreisen, en slags skuffelse over at vi ikke fikk programmene våre til å kjøre. Dette som skulle blitt hele reisens høydepunkt. Vi får dessverre ikke tatt noen kule bilder eller videoer å vise dere, ingen grensesprengende tall eller analyse på resultater fra metodene vi bruker. I mens vi sitter på raketten og surmuler på vei til planeten, grubler jeg på hvordan forskerne i IPA gjorde dette mulig for oss. Hvordan får dem raketten vår inn i en stabil bane? Hvordan finner de tallene som forteller oss hvor stabil bane vi er i? Det hele virker nesten litt magisk for meg for øyeblikket, og jeg tar frem tegnebrettet for å drepe dødtiden mellom avreisepunkt og destinasjonspunkt, og prøver å finne ut av hvordan vi skulle løst denne problemstillingen.
