☠☠☠ Advarsel ☠☠☠
I dette innlegget kan det komme en del likninger, som skal gi oss informasjon om ellipsebanen vår rundt planeten. Dere er dermed advart, og jeg skal selvfølgelig prøve å forklare så godt jeg kan hvordan vi resonnerer.
En del viktige likninger
Vi er i bane rundt planeten, men hvor stabil er denne banen? Det er interessant for oss å vite en god del ting om banen vår, slik at vi har nok informasjon til når vi skal lande. Dette kan for eksempel være hvor stor halvaksene våre er, som forteller oss noe om formen på banen vår. Dersom store halvakse er kjempestor, og lille halvakse er kjempeliten (se Figur 1 for eksempel), betyr jo det at vi er i en ganske utstrakt ellipsebane, som betyr at vi vil ha ganske høy hastighet i nærheten av planeten (i lille halvakse), og ganske lav hastighet langt unna planeten (i store halvakse).
Egentlig skulle vi funnet verdier for \(v_r,\;v_{\theta},\;\text{og}\;r\), men siden IPA har laget programmet for oss, kan vi tenke at vi allerede har tilgang på disse verdiene. Foreløpig holder vi det generelt og bruker ingen verdier, kun symboler. Her er en del likninger vi kommer til å få bruk for:
\((1)\hspace{1cm}v_r = \frac{x\cdot v_x + y\cdot v_y}{\sqrt{x^2 + y^2}}\)
\((2)\hspace{1cm}v^2 = v_r^2 + v_{\theta}^2 = v_x^2 + v_y^2 \)
\((3)\hspace{1cm}E_{tot} = \frac{1}{2}\hat{\mu}v^2 - \frac{\hat{\mu}m_g}{r}\), \(\hat{\mu} = \frac{Mm}{M + m} \approx m,\;\;m_g = G(M + m) \approx GM,\;\text{M >> m}\)
\((4)\hspace{1cm}a = \frac{\hat{\mu}m_g}{2|E_{tot}|} = \frac{GMm}{2|E_{tot}|}\)
\((5)\hspace{1cm}P^2 = \frac{4\pi^2a^3}{G(M + m)} \approx \frac{4\pi^2a^3}{GM}\)
\((6)\hspace{1cm}rv_{\theta} = b\sqrt{\frac{GM}{a}}\)
\((7)\hspace{1cm}e = \sqrt{1 - \left(\frac{b}{a}\right)^2},\;\;a>b\) (husk at hvis \(a<b\) så er b store halvakse og a lille halvakse og må bytte plass i likningen)
\((8)\hspace{1cm}r_A = a(1+e)\) (apoapsis, lengste avstand unna planet)
\((9)\hspace{1cm}r_P = a(1-e)\) (periapsis, korteste avstand unna planet)
Jeg kommer ikke til å utlede likningene, og noen av dem bør dere være kjent med fra tidligere innlegg som Planetbaner, Keplers lover, og Sol-dans og planet-vals. Andre likninger her kan det virke som at jeg trekker fra løse lufta, så jeg kan si kort hvor de kommer fra.
Den aller første likningen, likning (1) kommer fra å derivere posisjonsvektoren \(\vec{r}\) i polare koordinater. Dette ligger litt utenfor vgs-nivå, men kan være for de spesielt interesserte. Vi kan skrive posisjonen i polare koordinater som \(\vec{r} = r\vec{e}_r\), der både avstanden \(r\) og enhetsvektoren \(\vec{e}_r = (\cos\theta(t), \sin\theta(t))\) er funksjoner av tid. Deriverer vi \(\vec{r}\) vil vi få hastigheten gjennom produktregelen \(\vec{v} = \frac{dr}{dt}\vec{e}_r + r\frac{d\theta}{dt}\vec{e}_{\theta}\) der \(\vec{e}_{\theta} = (-\sin\theta(t), \cos\theta(t))\) er enhetsvektoren i tangentiell retning (kommer fra å derivere \(\vec{e}_r\)). Vi ser at hastighetskomponenten som går i radiell retning er \(v_r = \frac{dr}{dt}\). Vi husker at \(r = \sqrt{x(t)^2 + y(t)^2}\), så for å få den radielle komponenten \(v_r \) må vi derivere denne. Ved å derivere \(r = \sqrt{x(t)^2 + y(t)^2}\) ender vi opp med \(v_r = \frac{x\cdot v_x + y\cdot v_y}{\sqrt{x^2 + y^2}}\), som er likning (1).
Likning (4) kommer rett og slett fra den analytiske løsningen av tolegeme-problemet som du finner i dette innlegget, der vi finner størrelsen \(p=a(1-e^2)\). Deriverer vi den analytiske løsningen og kombinerer det med energilikningen, likning (3), kan vi også finne at størrelsen \(p\) også er \(p = \frac{\hat{\mu}m}{2E_{tot}}(e^2 - 1)\). Vi vet at i en ellipsebane så er \(E_{tot}<0\), så dermed vil for en ellipse \(p = \frac{\hat{\mu}m}{2E_{tot}}(1-e^2)\), og ved å sette disse to uttrykkene for \(p \) lik hverandre komme frem til likning (4).
MERK en ting fra likning (8) og (9). Ser vi på den analytiske løsningen av tolegeme-systemet kan vi se følgende:
\(r = \frac{a(1 - e^2)}{1 + e\cos\theta} = \frac{a(1 - e)(1 + e)}{1 + e\cos\theta}\)
Der vi har \(\theta = 0^\circ\) og \(\theta = 180^\circ\) kan vi se at vi får
\(r_P = \frac{a(1 - e)(1 + e)}{1 + e\cos(0)} = \frac{a(1 - e)(1+e)}{1 + e} = a(1-e)\), og følgende for
\(r_A = \frac{a(1 - e)(1 + e)}{1 + e\cos(180)} = \frac{a(1 - e)(1+e)}{1 - e} = a(1+e)\).
Likning (6) kommer fra bevaring av spinn og vis-viva likningen fra forrige innlegg. Ved litt manipulering av vis-viva likningen langs apoapsis og periapsis kan vi komme frem til uttrykket for spinn: \(L = mb\sqrt{\frac{GM}{a}}\). Vi vet at spinn kan skrives som \(L = mh\), der størrelsen \(h\) kan skrives \(h = r^2\omega\) der \(\omega\) er vinkelfarten. Vi kjenner også forholdet mellom vinkelfart og tangential fart, \(\omega = \frac{v_{\theta}}{r}\), setter inn i \(h\) og får \(h = rv_{\theta}\). Setter vi dette inn for \(L \) kommer vi frem til likning (6). Resten av likningene burde være kjente identiteter, og Keplers 3 lov i likning (5).
En full utledning av vis-viva likningen og likning (6) kan du finne på denne linken her.
Hvordan finner vi størrelsene?
Du skal se nå at rekkefølgen jeg satte opp likningene tidligere ikke var helt tilfeldig, fordi på akkurat den måten, i samme rekkefølge, kan vi finne størrelsene vi er interessert i å finne.
Programmet til IPA gir oss følgende informasjon:
- Hastighet \(\vec{v} = (v_x, v_y, v_z)\) i forhold til planeten
- Posisjon \(\vec{r} = (x, y, z)\) i forhold til planeten
- Tidspunktet \(t\) hastighet og posisjon er målt i.
Vi holder oss kun i xy-planet, så \(v_z\) og \(z\) er begge forholdsvis 0. Våre verdier er \(\vec{v} = (0, 1961,0) m/s\), \(\vec{r} = (2861743.6,0,0)m\) og at vi er i tiden \(t=0\). Dette kan føre til forenklinger, men likningene og prosessen vi gjør gjelder helt generelt. La oss ta dette stegvis.
Steg 1: Vi starter med likning (1) for å finne radiell hastighetskomponent \(v_r \). Vi får at \(v_r = 0\).
Steg 2: Vi bruker likning (2) til å finne total fart \(v\) ved å bruke at \(v^2 = v_x^2 + v_y^2\). Dermed skriver vi om likningen slik at vi kan finne \(v_{\theta}\) ved \(v_{\theta} = \sqrt{v^2 - v_r^2}\). Dermed får vi at \(v_{\theta}=1961m/s\).
Steg 3: Vi bruker likning (3) til å regne ut den totale energien \(E_{tot}\). Verdiene våre her for \(M\) og \(m\) er da \(M = 1.65\cdot 10^{23}kg\) som er planetens masse og \(m = 1100kg \) som er romskipets masse (kan være \(\pm\) drivstoff, men ikke så mye at vi for store avvik). Vi bruker likning (3) og får at vår totale energi er \(E_{tot} = -2114872820.77J\).
Steg 4: Vi følger rekkefølgen slavisk, og bruker likning (4) nå til å finne store halvakse, og får at store halvakse er \(a = 2861874.895m\).
Steg 5: Nestemann i rekka er Keplers 3 lov fra likning (5), som skal vi oss omløpstiden rundt planeten, \(P = \sqrt{\frac{4\pi^2a^3}{GM}}\), som spytter ut en verdi \(P = 9170s\), eller sagt på en greiere måte, \(P=2.5hr\).
Steg 6: Dette begynner å bli litt trettende, men vi holder ut. Vi bruker likning (6) og skriver om slik at vi kan løse for \(b\). Dette gir oss likningen \(b = rv_{\theta}\sqrt{\frac{a}{GM}}\), og husk at \(r = \sqrt{x^2 + y^2} = 2861743.6m\). Da får vi at lille halvakse er \(b = 2861874.892m\) (merk at store og lille halvakse er nesten helt like)
Steg 7: Blir da å finne eksentrisitet i ellipsebanen vår, ved å bruke likning (7), \(e = \sqrt{1 - \left(\frac{b}{a}\right)^2}\) (merk at her har vi a>b). Dette gir oss eksentrisiteten \(e = 4.59\cdot10^{-5}\).
Steg 8: Dette er endelig det siste steget, og vi skal her bruke likning (8) og (9) til å bestemme apoapsis og periapsis. Setter vi inn informasjonen vi har samlet så langt, får vi at \(r_A = 2862006.19m\) og \(r_P = 2861743.59m\).
Resultater
Så langt er all informasjonen vi har funnet frem spredt utover 8 steg, så la meg samle det mest interessante i en oversiktlig tabell:
| Avstand fra planetens sentrum, \(r\) | \(2861743.6m\) |
| Radiell fart, \(v_r\) | \(0m/s\) |
| Tangentiell fart, \(v_{\theta}\) | \(1961m/s\) |
| Store halvakse, \(a\) | \(2861874.895m\) |
| Lille halvakse, \(b\) | \(2861874.892m\) |
| Eksentrisitet, \(e\) | \(4.59\cdot10^{-5}\) |
| Omløpstid i bane, \(P\) | \(9170s\) eller \(2.5hr\) |
| Apoapsis, \(r_A\) | \(2862006.19m\) |
| Periapsis, \(r_P\) | \(2861743.59m\) |
Basert på resultatene ligger vi i en rimelig stabil bane. Lengste og minste avstand på apoapsis og periapsis er ikke spesielt ulike hverandre, som tyder på at vi ligger i ganske så lik avstand fra planeten til gitte tidspunkter. Det bekrefter også størrelsene på halvaksene våre, som også er nesten identiske (helt opp til tredje desimal på meteren, altså \(mm\)!).
Eksentrisiteten vår er ganske liten, og om du husker det så betyr \(e = 0\) at man befinner seg i en sirkelbane. Med andre ord ligger vi i en ganske så nært sirkelbane. Resultatene i seg selv kan være nok så trette, så vi plotter banen vår rundt planeten for å ta en sjekk
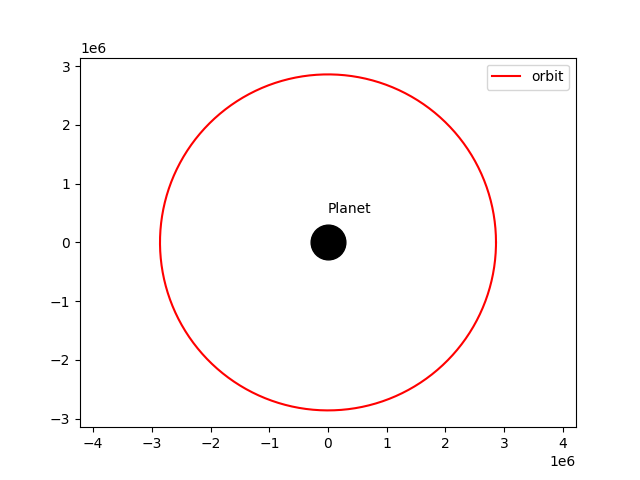
Med det blanke øyet kunne vi ikke skilt Figur 2 fra en helt ordinær sirkel (i alle fall ikke jeg).
En annen ting jeg ønsker å kommentere er at omløpstiden vår rundt banen ikke er spesielt lang. Ved første tanke kan man tenke seg at dette må være feil, men da er det fint å sammenlikne: ISS (International Space Station) bruker omtrentlig 90 minutter, altså 1.5 time på en runde rundt jorda. Det er 1 time mindre enn oss! Da ser vi plutselig at svaret vårt ikke er så urimelig likevel. Nå er planeten vi går rundt betraktelig mindre enn jorda (planeten vår har radius på 1 862km, jorda har 6 371km), men så ligger vi tross alt en del høyere også (vi ligger 2861km over planetens overflate, mens ISS ligger 408km over jordas overflate), så det er en slags trade-off mellom avstand og størrelse her.
Nøyaktighet
Her er det ikke så mye å ta av, annet enn at jeg valgte å se bort ifra romskipets masse. Mest på grunn av at jeg er litt usikker på hva massen er helt nøyaktig, ønsket jeg å bruke romskipets masse minst mulig, siden jeg ofte kunne se bort ifra den da den blir helt ubetydelig sammenliknet med planetens masse uansett (\(1100kg\) opp mot \(1.65\cdot10^{23}kg\), da trenger vi ikke å bry oss). Svarene hadde selvsagt blitt mer nøyaktige om jeg inkluderte det, men marginalt.
For å sjekke hvor konsistente tallene er, kjører vi noen runder rundt planeten, og gjentar hele prosessen for å finne ut. Jeg lar romskipet gå 5 ganger, som tilsvarer en tid \(t = 45850s\), eller omtrent \(13\) timer... Da får vi disse resultatene, representert i en liknende tabell:
| Avstand fra planetens sentrum, \(r\) | \(2861741.1m\) |
| Radiell fart, \(v_r\) | \(3.5\cdot10^{-6}m/s\) |
| Tangentiell fart, \(v_{\theta}\) | \(1961m/s\) |
| Store halvakse, \(a\) | \(2861872.379m\) |
| Lille halvakse, \(b\) | \(2861872.376m\) |
| Eksentrisitet, \(e\) | \(4.59\cdot10^{-5}\) |
| Omløpstid i bane, \(P\) | \(9169s\) eller \(2.5hr\) |
| Apoapsis, \(r_A\) | \(2862003.68m\) |
| Periapsis, \(r_P\) | \(2861741.07m\) |
som gir oss relative feil mellom denne tabellen og første tabellen:
Relative feil |
|
| Avstand fra planetens sentrum, \(r\) | \(8.79\cdot10^{-7}\) |
| Radiell fart, \(v_r\) | \(1.00\) |
| Tangentiell fart, \(v_{\theta}\) | \(4.40\cdot10^{-7}\) |
| Store halvakse, \(a\) | \(8.79\cdot10^{-7}\) |
| Lille halvakse, \(b\) | \(8.79\cdot10^{-7}\) |
| Eksentrisitet, \(e\) | \(1.19\cdot10^{-5}\) |
| Omløpstid i bane, \(P\) | \(1.32\cdot10^{-6}\) |
| Apoapsis, \(r_A\) | \(8.78\cdot10^{-7}\) |
| Periapsis, \(r_P\) | \(8.79\cdot10^{-7}\) |
Vi ser her at de relative feilene er bittesmå, som betyr at verdiene holder seg stabile. Det er verdt å kommentere feilen på den radielle farten \(v_r\): siden den først var \(0\), vil derfor den relative feilen på denne alltid være 1, siden vi alltid får \(\frac{|v_{r,1} - v_{r,2}|}{v_{r,2}} = \frac{|v_{r,2}|}{v_{r,2}} = 1.0\). Dermed vil alle feil på denne vises som høy relativ feil, selv om forskjellen mellom \(v_r\) skulle bli aldri så liten. Disse feilene kan komme av små numeriske feil, eller feil i simuleringene. Dermed er ikke denne noe vi bekymrer oss for, siden vi vet at verdien vi får for \(v_r\) etter 5 omløp er veldig liten.
Det viser seg at IPA manglet flere av tallene vi har funnet, og dermed sender vi tallene ned til dem slik at de også kan sørge for at vi får en trygg landing til den tid kommer, så ikke alt lener seg på oss. Vi kan dessverre ikke lande helt enda, da det er nødvendig for oss å analysere atmosfæren på planeten. Dette skal dere få vite mer om dersom dere leser dere inn på Del 6!