Vi faller rundt planeten. Etter hvert vil vi forsøke å entre atmosfæren og til slutt lande på planeten. Før vi kommer så langt, må vi forsikre oss om at orbiten vår er så sirkulær som mulig. La oss begynne med å se på likningen for orbit-hastighet. Når vi svever rundt en planet som vi gjør nå, er det kun én kraft som virker på oss. Tyngdekraften. Den gir oss en sentripetalakselerasjon. Vi har at
\(\sum F=F_G=\gamma\frac{mM_p}{r^2}\)
hvor \(\gamma, m, M_p, r\) er gravitasjonskonstanten, romskipets masse, planetens masse og avstanden fra romskipets massesenter til planetens massesenter. Videre får vi
\(\begin{align} \gamma\frac{mM_p}{r^2}&=m\frac{v^2}{r}\\ v&=\sqrt{\gamma\frac{M_p}{r}} \end{align}\)
Her har vi en formel for orbit-hastighet som funksjon av avstanden fra planetens sentrum. Plottet ser slik ut:
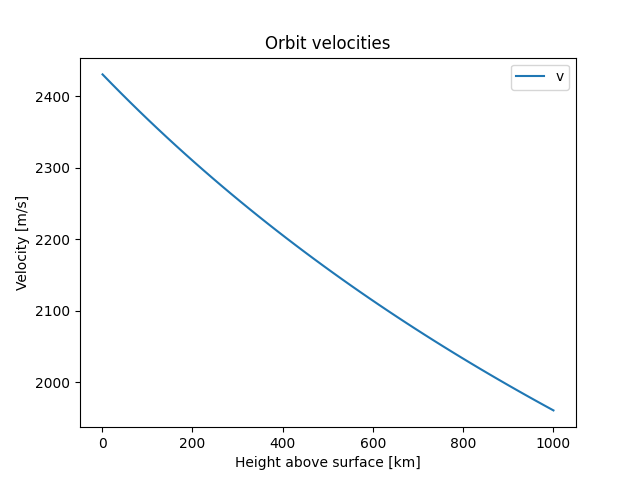
I Figur 1 går høyden fra 1 km til 1000 km over overflaten. Det er kanskje ikke så overraskende at vi trenger en lavere hastighet lenger vekk fra planeten?
Hva tror dere skjer om vi senker hastigheten? Jo, da vil vi entre en lavere orbit. Tilsvarende vil en hastighetsøkning resultere i en høyere orbit. Vi befinner oss for øyeblikket 1 000 km over overflaten. Vi regner ut hvilken hastighet vi har.
\(\begin{align} v&=\sqrt{6.674\cdot10^{-11}m^3kg^{-1}s^{-2}\frac{1.647\cdot10^{23}kg}{2.862\cdot10^6m}}\\ &\approx1960\,m/s \end{align}\)
Merk at her må vi legge til planetens radius for å få riktig avstand fra sentrum. Siden vi er veldig langt unna å treffe atmosfæren, kan vi bremse for å komme i lavere orbit. Vi ønsker å synke til vi er 400 m over overflaten, som er omtrent samme høyde som den internasjonale romstasjonen, ISS, befinner seg på. Vi får nå en hastighet på ~ 2205 m/s.

Vi stiller inn kameraet slik at vi får bildet vist på Bilde 1. Vi er nå såpass nærme planeten at vi kan begynne noen beregninger.
Det første vi vil starte med er å finne omløpstiden vår. Strekningen vi skal tilbakelegge blir omkretsen til sirkelen vi beveger oss langs. Vi vet hva avstanden vår er til sentrum av sirkelen, og hvilken hastighet vi har. Fra bevegelseslikningen for konstant hastighet har vi at \(s=v\cdot t\). Strekningen blir \(2\pi r\) og hastigheten vår er orbit-hastighet. Vi regner ut omløpstiden vår, \(T\):
\(\begin{align} T&=\frac{2\pi r}{v}\\ &=\frac{2\pi\cdot2.262\cdot10^6m}{2.206\cdot10^3m/s}\\ &\approx6442.565\,s \end{align}\)
Vi bruker altså omtrent 1 time og 50 min på å fullføre én runde rundt planeten. La oss forsøke å filme litt av hva vi ser. Det holder vel å filme den siden av planeten det er lys på, er dere ikke enige?

Videoen over er speedet kraftig opp. Vi faller egentlig i ~6 000 sekunder, som tilsvarer litt over halvannen time. Ganske kult, ikke sant?
Det neste vi skal sjekke er at vi holder en jevn høyde over overflaten. Vi ønsker en så sirkulær bane som mulig. Det er fordi når vi skal i lavere orbit er det lettere å utføre en kontrollert manøver ved sirkulære baner. Nå kan romskipet vårt falle fritt en runde rundt planeten, og vi måler avstanden til bakken under oss hvert kvarter. Dette er resultatene vi får:
| Tid (s) | Avstand (m) |
| 0 | 400206.95 |
| 900 | 400169.40 |
| 1800 | 400012.41 |
| 2700 | 400157.53 |
| 3600 | 400019.98 |
| 4500 | 400188.14 |
| 5400 | 400197.00 |
Som vi ser så er ikke banen vår helt sirkulær, men det skal gå helt fint. Nå skal vi gå ett steg videre. I et ideelt scenario kan vi ta noen bilder av bakken under oss og se om vi finner noen potensielt gode landingssteder. Det eneste som kan korrumpere vår geniale plan er at planeten spinner om sin egen akse, og dermed vil også landingsstedet vårt endre posisjon med tiden.
Heldigvis for oss vet vi hvor lang tid planeten bruker på å snurre en gang rundt sin egen akse, også kalt perioden, \(T_p\) til planeten. Den bruker ~11.15 dager, som tilsvarer 11 dager, 3 timer og 36 minutter. Vi kan bruke dette til å regne ut vinkelfarten \(\omega\). Formelen er gitt ved
\(\begin{align} \omega=\frac{2\pi}{T_p} \end{align}\)
som gir en vinkelfart på \(6.52\cdot10^{-6}\) radianer per sekund. Planeten vår roterer med andre ord om z-aksen, med null helning. Til sammenlikning har jorda en helning på ~23.5°. Jordas helning sørger for at dere har årstider. I vårt solsystem har alle planetene null helning.
Det letteste vi kan gjøre er å finne en landingsplass på planetens ekvator. Der vet vi hva vinkelfarten er, og vi kan lett beregne hvordan det punktet flytter seg med tid. Ettersom at vi kan måle avstanden vår til planetens sentrum til en hver tid, kan vi trekke fra radien til planeten for å finne den radielle komponenten til posisjonen i sfæriske koordinater.
Oppfriskning i sfæriske koordinater. Hvis dere vil ha enda mer oppfriskning, kan dere se innlegget om stereografisk projeksjon her. Her har vi tre ortogonale komponenter til posisjonen, gitt ved
\(\begin{align} \vec{r}&=(\rho,\theta,\varphi)\\ 0&\leq\rho\leq\infty\\ 0&\leq\theta\leq\pi\\ 0&\leq\varphi\leq2\pi \end{align}\)
Siden langingsplassen vil ligge langs ekvator, vil det kun være \(\varphi\)-komponenten som endrer seg med tid. \(\theta\) vil være konstant lik \(\frac{\pi}{2}\). Koordinatene vi får fra instrumentene om bord er kartesiske. Heldigvis er ikke overgangen så vanskelig, bare se selv.
\(\begin{align} \rho&=\sqrt{x^2+y^2+z^2}\\ \theta&=\arccos\Bigg(\frac{z}{\sqrt{x^2+y^2+z^2}}\Bigg)\\ \varphi&=\arctan\bigg(\frac{y}{x}\bigg) \end{align}\)
Langs ekvator har vi konstant hastighet, så vi kan beregne koordinatet til landingsplassen vår som funksjon av tid.
\(\begin{align} \vec{r}(t)=\Big(\rho-R_p, \frac{\pi}{2}, \varphi(t)\Big) \end{align}\)
Ettersom at den radielle komponenten alltid er på overflaten, trenger vi kun å finne et uttrykk for \(\varphi(t)\). Dette er en vinkel, så vi kan enkelt skrive den slik:
\(\varphi(t)=\varphi_0+\omega\cdot t\)
Dette gir posisjonen som funksjon av tid:
\(\begin{align} \vec{r}(t)=\bigg(R_p\,,\,\frac{\pi}{2}\,,\,\varphi_0+\omega\cdot t\bigg) \end{align}\)
For å komme oss tilbake til kartesiske koordinater følger vi følgende oppskrift:
\(\begin{align} x&=\rho\sin\theta\cos\varphi\\ y&=\rho\sin\theta\sin\varphi\\ z&=\rho\cos\theta \end{align}\)
Ettersom at \(\rho\) og \(\theta\) er konstante, kan vi skrive det slik:
\(\begin{align} x&=R_p\cos\varphi\\ y&=R_p\sin\varphi\\ z&=0 \end{align}\)
La oss nå falle rundt planeten igjen, og ta noen bilder av dagsiden planeten. Vi noterer også posisjonene i sfæriske koordinater.










Dette ble mange bilder! Klarer dere å se noe? Det er kanskje litt vanskelig, men det er lett å se at dette ser ut som en ørkenplanet. Ikke ulikt Mars. Grunnen til at vi vil se på dette er for å forsikre oss om at vi ikke lander på et fjell eller liknende. Det er som sagt vanskelig å se noe, men vi holdt ord og tok målinger ved hvert bilde. Under kommer en tabell med tid og posisjon for hvert punkt direkte under oss da bildet ble tatt (midt i bildene).
| Bilde # | Tid (s) | Posisjon \((\rho,\theta,\varphi)\) |
| 1 | 0 | \((R_p\,,\,\frac{\pi}{2}\,,\,-0.88)\) |
| 2 | 300 | \((R_p\,,\,\frac{\pi}{2}\,,\,-0.59)\) |
| 3 | 600 | \((R_p\,,\,\frac{\pi}{2}\,,\,-0.29)\) |
| 4 | 900 | \((R_p\,,\,\frac{\pi}{2}\,,\,\sim0)\) |
| 5 | 1200 | \((R_p\,,\,\frac{\pi}{2}\,,\,0.29)\) |
| 6 | 1500 | \((R_p\,,\,\frac{\pi}{2}\,,\,0.58)\) |
| 7 | 1800 | \((R_p\,,\,\frac{\pi}{2}\,,\,0.88)\) |
| 8 | 2100 | \((R_p\,,\,\frac{\pi}{2}\,,\,1.17)\) |
| 9 | 2400 | \((R_p\,,\,\frac{\pi}{2}\,,\,1.46)\) |
| 10 | 2700 | \((R_p\,,\,\frac{\pi}{2}\,,\,-1.39)\) |
La oss se nærmere på Bilde 8.

I midten av dette bilde kan vi se at landskapet ser ganske flatt ut. Vi kommer naturligvis ikke til å klare å lande nøyaktig der vi ønsker, men det hadde vært fint om vi kom i nærheten. Ikke fordi vi anser oppdraget som feilet dersom vi ikke får det til, men det vil være en ekstra boost av selvtilliten om vi klarer å lande der vi ønsker. La oss nå se hvordan formelen for dette landingspunktet blir. Fra tabellen har vi at \(\varphi_0=-0.88\). Dermed kan vi bruke formelen vår til å finne ut av hvilken posisjon punktet har etter en gitt tid.
\(\begin{align} \vec{r}(t)=\bigg(R_p\,,\,\frac{\pi}{2}\,,\,-0.88+\omega\cdot t\bigg) \end{align}\)
Vi setter inn uttrykket vi har for \(\omega\).
\(\begin{align} \vec{r}(t)=\bigg(R_p\,,\,\frac{\pi}{2}\,,\,-0.88+6.52\cdot10^{-6}\cdot t\bigg) \end{align}\)
Den generelle formelen kommer vi til å få bruk for senere. Foreløpig er vi litt for høyt oppe til å kunne si noe veldig nøyaktig om landskapet under oss. Men det hadde som sagt vært gøy å få til å lande omtrent der vi ønsker.
I neste innlegg skal vi prøve å modellere atmosfæren til planeten. Dette kommer til å være viktig for å kunne si noe om hvordan luftmotstanden vil være for landingsfartøyet vårt.
