Hva slags gass finnes?
Som du kanskje har skjønt skal vi modellere atmosfæren på planeten vi skal lande på. Det første steget i denne retningen er å finne ut hva atmosfæren faktisk består av, og hvor mye av hvert stoff. Det finnes ganske mange stoffer i denne store galaksen, så jeg kaster inn en tabell med stoffer (gass) som er vanlige å finne i atmosfærer:
| Gass | Masse |
|---|---|
| \(O_2\) (oksygengass) | \(5.352\cdot 10^{-26}kg\) |
| \(H_2O\) (vann) | \(3.010\cdot 10^{-26}kg\) |
| \(CO_2\) (karbondioksid) | \(7.359\cdot 10^{-26}kg\) |
| \(CH_4\) (metangass) | \(2.676\cdot 10^{-26}kg\) |
| \(CO\) (karbonmonoksid) | \(4.683\cdot 10^{-26}kg\) |
| \(N_2O\) (lystgass) | \(7.359\cdot 10^{-26}kg\) |
Dette er da gassene vi antar kan befinne seg i atmosfæren til planeten, og er de gassene vi kommer til å bygge modellen på. Men hvordan finner vi ut av hva slags gass atmosfæren på en helt ukjent planet består av?
Spektralanalyse - The Dark side of the Moon
Det er på tide å introdusere dere for spektralanalysens verden! Vi analyserer spektrene på elektromagnetiske bølger som emitterer ut av gassen, og prøver å koble opp bølgelengden på disse strålene mot hvilket stoff vi har (forenklet, men vi kommer til analysen ivrig-per). Likt som med type gasser finnes det mange bølgelengder, så jeg slenger ved enda en tabell som forteller oss hvilke spektrallinjer som er vanlige å finne for hvert av stoffene vi har i en atmosfære:
| Gass | Spektrallinjer [nm] \((10^{-9}m)\) | ||
|---|---|---|---|
| \(O_2\) | 632 | 690 | 760 |
| \(H_2O\) | 720 | 820 | 940 |
| \(CO_2\) | 1400 | 1600 | ----- |
| \(CH_4\) | 1660 | 2200 | ----- |
| \(CO\) | 2340 | ----- | ----- |
| \(N_2O\) | 2870 | ----- | ----- |
De blanke boksene betyr bare at ikke alle stoffene nødvendigvis har 3 spektrallinjer.
Da kan vi endelig prøve å kjøre i gang litt analyse! Vi trenger bare et par forberedelser først: siden vi reiser i romskipet vårt med en eller annen hastighet kommer alle målte bølgelengder å bli forskjøvet med det vi kaller Doppler skiftet, og vi må derfor ta dette i betraktning når vi skal måle spektrallinjer. For de av dere som trenger å friske opp, måles Doppler skiftet med denne likningen:
\(\begin{align*} \frac{\Delta\lambda}{\lambda_0} = \frac{v_r}{c} \end{align*}\)
som forteller oss at forholdet mellom forskjellen i målt bølgelengde \(\lambda\) og laboratoriemålt bølgelengde \(\lambda_0\) (\(\Delta\lambda\)) og den laboratoriemålte bølgelengden \(\lambda_0\) er lik forholdet mellom romskipets fart i radiell retning \(v_r\) og lyshastigheten \(c\). Dette er en meget nyttig sammenheng som dukker opp i flere tilfeller. Vi trenger blant annet denne sammenhengen for å gjøre vår analyse, siden den spiller en rolle i hva slags bølgelengder vi kommer til å observere på romskipet vårt.
Videre antar vi dermed at farten \(10km/s\) for romskipet relativt til planeten er den absolutt øvre grense for romskipets fart. Da kan vi resonnere oss til det maksimale Dopplerskiftet vi kan klare å oppnå, som blir nyttig videre i analysen. Vi tenker oss at dersom vi så vidt er nedom og snitter atmosfæren, og tar målinger rett foran romskipet, kan vi teoretisk sett klare å måle bølgelengder der vi får dopplerskift med farten \(v=10km/s\). Bølgelengdene vi måler da vil bli kortere enn det den er i virkeligheten, siden vi da reiser mot bølgelengden vi måler (tenkt sett). Putter vi dette inn i formelen for dopplerskift får vi at den maksimale forskyvningen \(\Delta\lambda\) vi kan få er
\(\begin{align*} \Delta\lambda_{max} = \frac{v}{c}\lambda_0 \approx -3.335\cdot10^{-5}\lambda_0 \end{align*}\)
Dersom vi gjøre samme måling, men bak oss i stedet for foran oss vil vi få et Dopplerskift der bølgelengdene vi måler er lengre enn det de er i virkeligheten. Da vil vi få samme \(\Delta\lambda_{max}\), men med motsatt fortegn, altså
\(\begin{align*} \Delta\lambda_{max} = \frac{v}{c}\lambda_0 \approx 3.335\cdot10^{-5}\lambda_0 \end{align*}\)
Doppler-skiftet forteller oss altså at dersom vi har en hastighet relativt til en stråle med en eller annen bølgelengde \(\lambda_0\), vil vi observere en bølgelengde \(\lambda\) som er blitt forskjøvet med en forskyvning \(\Delta\lambda\), som vi må ta hensyn til. Vi må nå bestemme oss for hvordan vi skal klare å måle hvilke stoffer vi har i atmosfæren. Så langt vet vi at vi ser etter noe som har med bølgelengder å gjøre... Hva kan det være?
*----💡💡💡💡💡💡💡💡💡----* Bingo!
Som en av mine (selvfølgelig min, ikke noen andre sin) genistreker finner jeg ut at vi skal se på fluksen av de ulike elektromagnetiske strålene vi får inn, siden det der finnes et triks i ermet. Hvis fluks er ukjent for deg, skal jeg gi en veldig kjapp forklaring:
Fluks er et mål på hvor mye av en ting som går gjennom en flate av noe pr. sekund.
La meg ta et eksempel: Dersom du står på kjøkkenet, og beveger deg gjennom døra inn til stua, har det nå vært en fluks gjennom døra di på ett menneske pr. dørareal pr. sekund i akkurat det øyeblikket du passerer gjennom. Dersom du og pappaen din går gjennom døra samtidig, var fluksen i akkurat det øyeblikket to mennesker pr. dørareal pr. sekund. Dersom ingen går gjennom døra er det fluks på null mennesker pr. dørareal. pr. sekund. Det vi må passe oss litt for er at fluks kan ha en slags retning. Det vil si hvilken vei man definerer som positiv retning for fluksen. Definerer vi fra kjøkkenet til stua som positiv retning, vil vi ha positiv fluks om du går gjennom døra fra kjøkkenet til stua. Men dersom du beveger deg gjennom døra fra stua til kjøkkenet da, vil vi ha en negativ fluks gjennom døra. Håper du fikk litt bedre feeling på hva fluks er nå.
Tilbake til fluksen i spektralanalysen: Vi tenker oss nemlig nå at gassen i atmosfæren er ideell gass, (husker du ikke hva ideell gass er så klikk på denne linken og les litt om det fra en tidligere bloggpost). Husker du hva det betyr? Det betyr at hastigheten til gasspartiklene er Gaussisk fordelt! Ta litt vare på denne tanken om en Gaussisk hastighetsfordeling litt til, så skal vi gi denne fluksen litt mer shine. Vi kjører et lite tankeeksperiment:

Se for deg at vi (1) har en strålingskilde, (2) oss som skal måle strålingen, og (3) en sky av gass mellom oss og strålingskilden. Vi tenker oss først at alle gasspartiklene står i ro, uten noen form for bevegelse. Strålingen vi prøver å måle treffer denne gasskyen før den treffer oss, som vil absorbere stråling med en bølgelengde som tilsvarer forskjellen mellom energinivåene i gass-atomet. Dermed får vi en syltynn sort linje i absorpsjonsspekteret vårt, på akkurat den bølgelengden. Men vent, det er mer, for det blir faktisk ikke en syltynn sort linje, men en passe tjukk sort linje. Holdt du godt på tanken om at gassen hadde Gaussisk hastighetsfordeling? I så fall medalje til deg 🥇. Vi tenker oss nå at gassen har en hastighet (som den faktisk har). Denne hastigheten vil resultere i et slags "omvendt dopplerskift" (om jeg kan kalle det for det?) der den absorberer stråling med bølgelengde som er skiftet med dopplerskiftet korresponderende til farten partikkelen har! Altså får partikkelen en fart relativt til strålen som treffer den, og tillater dermed å absorbere stråler med litt forskjøvne bølgelengder. Siden gassen har en Gaussisk fordeling av hastighet, vil også de ulike bølgelengdene som absorberes også få en Gaussisk fordeling!
Men hva i alle dager har dette med fluks å gjøre? Jo, dette påvirker jo strålingsfluksen vi måler, siden vi nå vil måle mindre stråling med bølgelengdene som blir absorbert pr. areal pr. tid! Ser vi på kurven for fluks pr. bølgelengde \(F(\lambda)\) vil vi da få et opp-ned Gaussisk plot (siden vi mangler fluks på den bølgelengden), som kan hjelpe oss på vår vei i analysen.
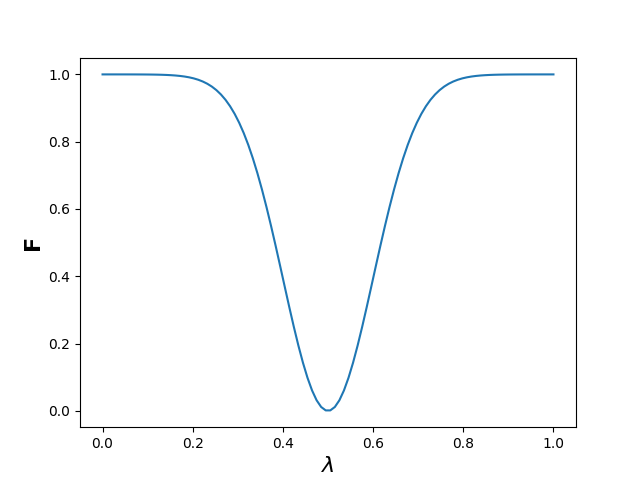
Med en slik Gaussisk linjeprofil på fluksen, kan vi skrive fluksmodellen vår nå på formen
\(F(\lambda) = F_{cont}(\lambda) + (F_{min} - F_{cont(\lambda)})e^{-\frac{1}{2}\left(\frac{\lambda - \lambda_0}{\sigma}\right)^2}\)
der \(F_{cont}(\lambda)\) er kontinuumsfluksen (fluksen vi hadde sett dersom all absorpsjonen var borte), \(F_{min}\) er verdien på bunnpunktet i den Gaussiske linjeprofilen (fluksverdien vi mister mest av), \(\lambda_0 \) er bølgelengden som absorberes mest (\(F(\lambda_0) = F_{min}\)) og \(\sigma\) er standardavviket (dersom du husker lite av disse sannsynlighetsgreiene anbefaler jeg deg virkelig å lese på denne linken).
Det neste steget nå er å finne et uttrykk for standardavviket i linjeprofilen, og det skal vi gjøre kjapt og enkelt for dere. Vi slenger rett og slett et stykke god informasjon på koldtbordet, og tar det derfra. Vi henter frem fra lærebøkene at \(FWHM\) for denne fluksmodellen er
\(FWHM = \frac{2\lambda_0}{c}\sqrt{\frac{2kT\ln2}{m}}\)
der \(k \) er Boltzmann konstant, \(T\) er gassens temperatur målt i Kelvin, og \(m\) er massen til et gassmolekyl av gassen vi ser etter. Vi har en snedig liten relasjon mellom \(\sigma\) og \(FWHM\) som er
\(\sigma = \frac{FWHM}{\sqrt{8\ln2}}\)
som med litt formelmagi gir oss uttrykket for standardavviket
\(\sigma = \frac{2\lambda_0}{c}\sqrt{\frac{kT}{4m}}\)
Med dette har vi alt redskapet vi trenger for å analysere atmosfæren, livet går fritt og fint, og herifra kan ingenting gå galt!
Dataanalyse - dette går skikkelig galt
Ikke la deg skremme av overskriften, dette skal gå fint (enn så lenge). Vi har fastmontert noen apparater fra IPA som skal ta nødvendige datamålinger for oss. Det er veldig viktig å nevne at absolutt ALL DATA har blitt normalisert, slik at \(F_{cont}=1\). Måling av data som blir gjort er
- \(F\), fluks målt fra atmosfære
- \(\lambda\), målte bølgelengder på fluksen [nm]
- \(\sigma_{støy}\), Gaussisk støy vi har fått på toppen av fluks-dataen
Dersom vi prøver å plotte frem et lite utklipp av fluksen på bølgelengden i intervallet \([\lambda_0 - \Delta\lambda_{max}, \lambda_0 + \Delta\lambda_{max}]\)for \(N_2O\) med \(\lambda_0=2870nm\), får vi dette plottet:
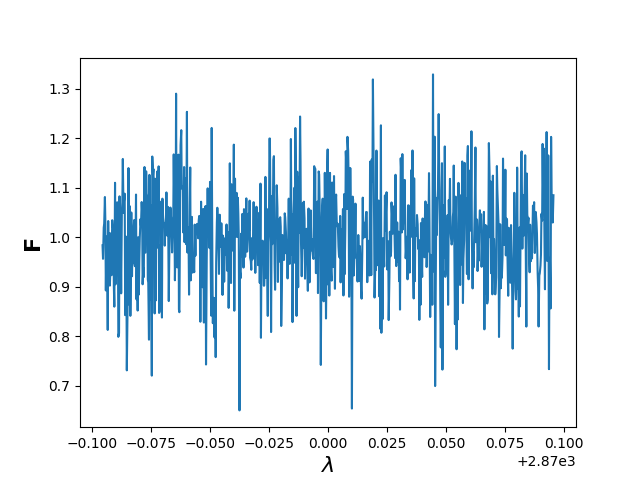
Oi, dette var stygg data å se på! Dermed bretter vi opp ermene og setter i gang til verks. Vi trenger fortsatt et par verktøy til i verktøy-kassa for å kunne analysere denne type data. Det første vi må kunne er hvordan vi faktisk skal finne ut av hva vi skal se på, og hvordan vi finner riktige parametere til modellen vår for fluks, som skal fortelle oss hva slags gass vi har i atmosfæren. Vi starter med førstnevnte, og ser kjapt videre på noe vi kaller \(\chi^2\)-metoden (storebror til minste kvadraters metode):
Lynkurs i å spotte kurver
Vi kan starte med dette plottet, som er for \(H_2O\) med \(\lambda_0=820nm\), og se etter hva som er interessant.
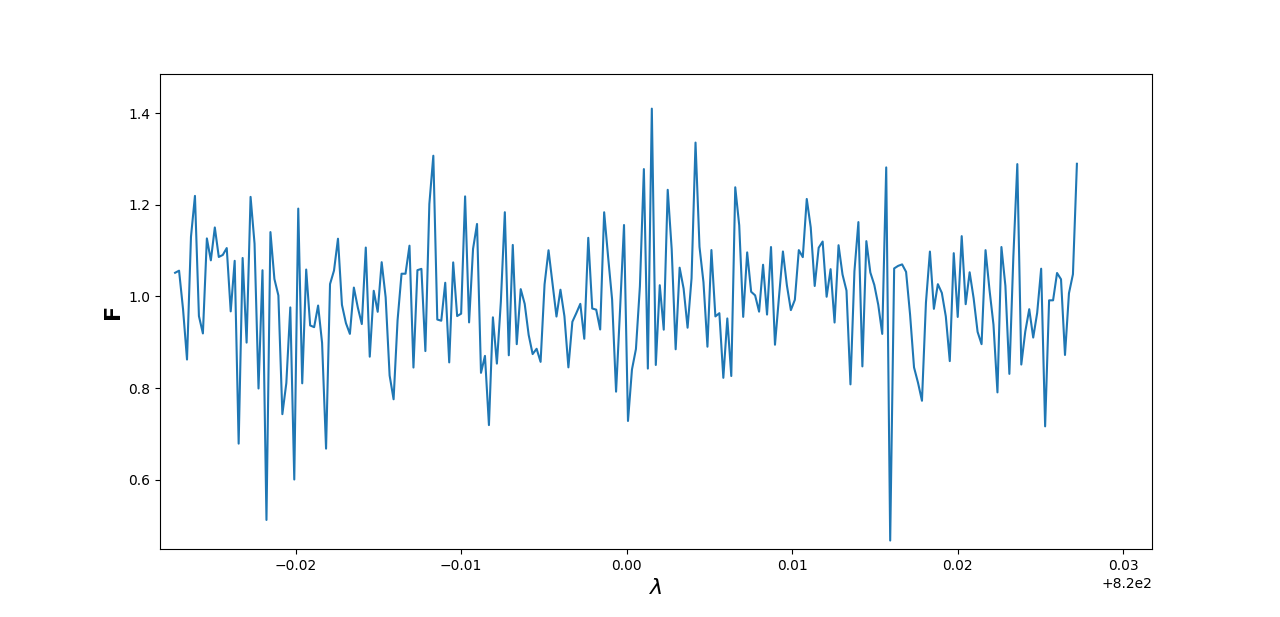
I alt dette støyet, leter vi etter noe som kan tyde på en Gaussisk linjeprofil. En annen viktig ting vi ser etter, er at \(F_{min}\) skal være lav, dvs. at spikes som stikker dypt nedover i grafen helst er mindre enn \(0.7\), fordi det betyr at det forsvinner en del fluks ut her. Husk at dataen er normalisert. Det jeg først og fremst gjør da er å zoome inn på venstresiden av plottet, og scrolle meg bortover mot høyre for å se om jeg finner en slik profil. På dette plottet ser jeg allerede et par steder som interesserer meg, som jeg skal ringe ut:
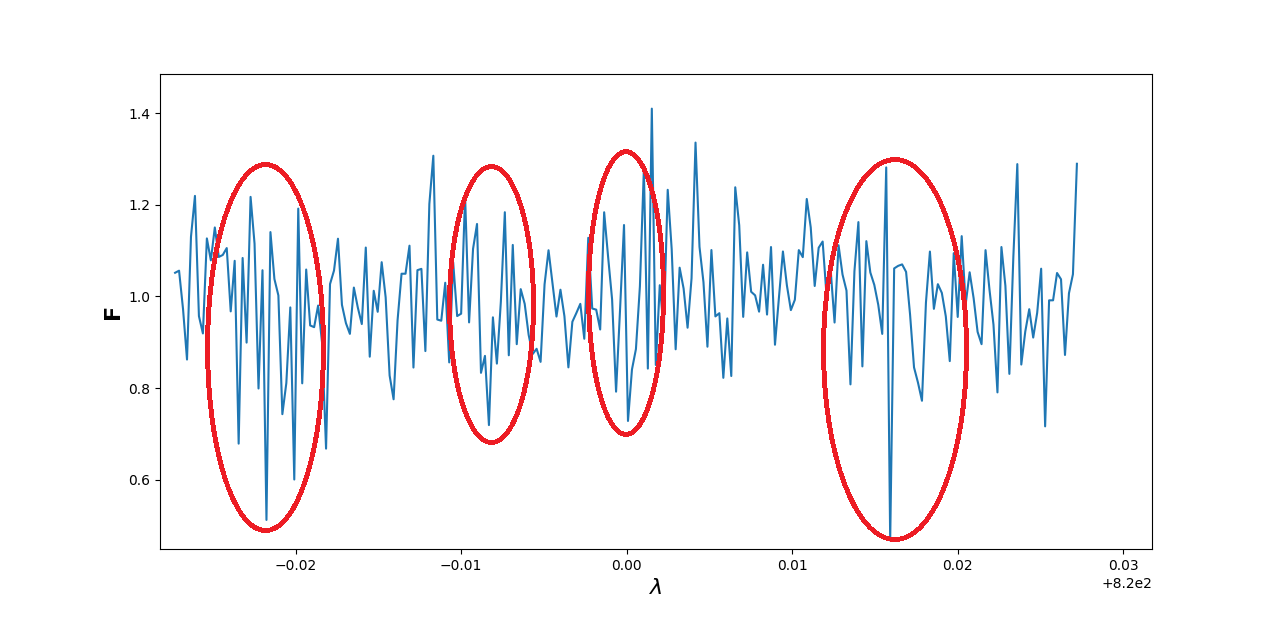
Disse stedene er interessante på grunn av enten dype spikes, eller på grunn av Gaussisk linjeprofil. Da zoomer jeg inn på disse områdene, og skriver ned hva bølgelengden \(\lambda_{obs}\) er på disse områdene.
Superlynkurs i \(\chi^2\)-metoden
\(\chi^2\) er ikke særlig vanskeligere enn minste kvadraters. Du husker kanskje at minste kvadraters metode ble skrevet slik:
\(\Delta = \sum_\limits{i}(F_{real,i} - F_{model}(t_i))^2\)
og \(\chi^2\) er bare en liten justering til det:
\(\chi^2 = \sum_\limits{i}\left(\frac{F_{real,i} - F_{model}(t_i)}{\sigma_{støy,i}}\right)^2\)
Om du ikke la merke til det har vi delt på den målte datastøyen, og det er det hele. Grunnen til dette er fordi datastøyen ikke lenger er *omtrent* den samme i alle datapunkter, som var en forutsetning for minste kvadraters. Dermed må vi inkludere denne når den faktisk er forskjellig i alle datapunkter. Les mer om minste kvadrater her. Det vi da gjør er å variere parameterne \(F_{min}\), \(\lambda_0\) og \(\sigma \) i modellen vår får fluks \(F(\lambda)\), og finner det settet med parametere som gir oss den minste \(\chi^2\) som da sier oss noe om sannsynligheten for at dette stoffer er i atmosfæren.
Da kan vi endelig komme oss tilbake på sporet av dataanalysen. Idéen vår bak analysen er å lese av datakurvene for fluksen i et gitt intervall, og finne en bølgelengde et sted som er interessant for oss å undersøke. Videre gjør vi et parametersøk med \(\chi^2\)-metoden, som skal gi oss parameterne til modellen \(F(\lambda)\) som passer best med dataen i dette intervallet. Vi gjør dette for alle gassene på alle bølgelengdene vi har, og leser av resultatet fra \(\chi^2\) og modellen \(F(\lambda)\). Dermed bestemmer vi om det er sannsynlig at vi har den og den gassen i atmosfæren, og i så fall hvor mye av den vi har.
Jeg skriver opp en mer spesifikk oppskrift på hvordan vi skal gjøre det, som er selve metoden for hvordan vi går frem:
Oppskrift på analyse(1) Vi finner ut av hvilket stoff vi ønsker å se på, eksempelvis \(H_2O\), og finner frem alle tall vi har på denne gassen. Det er da typ. \(\lambda_0,\;\Delta\lambda_{max},\;m,\;\sigma\) og antar en temperatur \(T\) for denne gassen et sted mellom \(150-450K\). (2) Vi plotter frem et slikt plott av fluksen slik som vi har gjort ovenfor i intervallet \([\lambda_0 - \Delta\lambda_{max}, \lambda_0 + \Delta\lambda_{max}]\) og zoomer vi inn og leter etter områder som kan likne på profiler vi leter etter. Vi ser på områder som strekker seg langt ned på grafen eller områder med Gaussisk profil. Finner vi et interessant område skriver vi ned bølgelengden \(\lambda_{obs}\) som kan se ut som \(\lambda_0\) i linjeprofilen. (3) Etter å ha notert ned bølgelengden \(\lambda_{obs}\) på området vi syntes ser interessant ut (gjerne det som kan se ut som \(\lambda_0\) i modellen) finner vi hvilke parameterverdier \(F_{min},\;\sigma,\;\lambda_0\) som gir oss den modellkurven \(F(\lambda)\) som som passer best inn med fluksdataen i intervallet vi ser på ved å bruke \(\chi^2\)-metoden. Dette skal fortelle oss hvor sannsynlig det er at gassen vi ser på befinner seg i atmosfæren vår. Vi gjentar dette for alle gassene på alle bølgelengdene vi forventer. |
Hvor skal vi lete?
Jeg har så langt snakket om parametersøk med \(\chi^2\)-metoden, men vi kan jo ikke søke oss gjennom uendelig mange parametere. Vi er nødt til å begrense oss, så dermed er vi nødt til å bestemme et par intervaller. Det er vanlig å se etter en \(F_{min}\in[0,\;0.7]\), siden verdier over det er så små at det ikke er noe særlig som absorberes av gassen. Når vi leter etter \(\lambda_0\) bruker vi standardavviket \(\sigma\) som vi regnet ut tidligere, og leter i et område rundt \(\lambda_0\in[\lambda_{obs} - 3\sigma, \lambda_{obs} + 3\sigma]\), siden vi får med oss \(99.7\%\) av bølgelengdene som kan være kandidater for beste modell (66, 95, 99.7 - regelen fra statistikken). For å finne hvilken \(\sigma\) som passer best inn i modellen leter jeg i intervallet \(\sigma\in[0,\;3\sigma]\). MERK også at jeg blander to ulike \(\sigma\) om hverandre her, den ene \(\sigma\) er en parameter i modellen vår \(F(\lambda)\), mens den andre \(\sigma\) er standardavviket i en tenkt flukskurve for en type gass. Det er viktig å holde forskjell på dem. Dette gjør jeg fordi innen \(3\sigma\) har jeg dekket alle lambda som vil være inneholdt i linjeprofilen for denne gassen.
Resultat og diskusjon - det er her ting går jæskla skeis
Skal jeg være dønn ærlig her har vi ikke så mye resultater å vise til. Det vil si at vi ikke fikk til noen resultater å vise til. La meg forklare dere hvor galt det går:
Vi skal få et unikt sett med parametere \(F_{min},\;\sigma,\;\lambda_0\) som skal minimere \(\chi^2\)-metoden. Saken er bare den at vi får flere verdier for disse parameterne. Dermed er det vanskelig for oss å bestemme noen kurver, og i det hele tatt tolke noe som helst om noen av gassene og bølgelengdene vi forventer å ha i atmosfæren vår. I tillegg får vi at \(F_{min} = 0.7\) for alle gasser på alle bølgelengder, noe jeg syntes er veldig tvilsomt, som tyder på at noe med implementasjonen av koden i Python er gal. Vi har dratt oss i håret i ukesvis for å finne feilen, men til ingen nytte og med 50% av håret igjen. Vi er nødt til å se oss slått av atmosfæren. Dermed må vi finne på noe annet for å klare å lande, og vi skal prøve å finne ut av en strategi for dette.
Hva gjør vi da når ingenting går som det skal?
Det blir egentlig ikke så fryktelig komplisert, bare veldig kjedelig. Vi tenker oss at vi har den aller letteste atmosfæren, med den gassen som veier minst. Dette er en ekstremt pessimistisk og urealistisk antakelse, men dersom vi gjør dette og klarer å simulere en suksessfull landing vil vi klare å lande for en hvilken som helst annen sammensetning av atmosfæren siden den da vil være tyngre. En lett gass vil gjøre det lettere for oss å falle gjennom atmosfæren fordi den har lavere tetthet (eller tettheten er spredt lenger utover mot verdensrommet fra planetens overflate), som gjør det vanskelig for oss å bremse ned (og lettere å krasje). Dermed er det lite friksjonskrefter og trykk som virker på raketten og fallskjermen vi skal bruke til å lande med høyere opp i atmosfæren, som gjør det vanskelig for oss å lande siden det er lettere å krasje. Et annet ganske ille tilfelle ville også vært den tyngste gassen, som vil ha høy tetthet lavere ned i atmosfæren. Da er det enklere å lande, men lettere å brenne opp i atmosfæren underveis dersom hastigheten er for stor, siden tettheten stiger fortere på kort tid lavere i atmosfæren enn for den tynne gassen, som har det fordelt lenger utover mot verdensrommet. Vi har at den aller letteste gassen vi kunne ha med i atmosfæremodellen var \(CH_4\) (metangass) med masse \(m_{CH_4} = 2.676\cdot 10^{-26}kg\). Dermed vil den absolutt letteste sammensetningen av atmosfære være \(100\%\;CH_4\), som igjen er urealistisk. Det kan også være nyttig å teste den aller tyngste atmosfæren vi kan ha, som vil være laget av \(100\%\;N_2O\), slik at vi har testet og landet for begge worst-case scenarioer.
Klarer vi altså å lande i de begge mest ekstreme worst-case scenarioene med atmosfære av \(100\%\;CH_4\) eller atmosfære av \(100\%\;N_2O\) vil vi også klare å lande i alle atmosfærer som befinner seg mellom disse to. Det er surt å gjøre det så kjedelig, men vi må likevel bare ta det med oss og teste denne atmosfæresammensetningen, i all uviten om hva den ekte atmosfæren består av. Hvem vet, kanskje vi en dag vil finne ut, men i nærmeste fremtid har vi viktigere ting å finne ut av. Finn ut hva på neste blogginnlegg.
Forrige innlegg << Neste innlegg >>
