Atmosfæriske differensiallikninger
Vi skal nå bygge vår egen atmosfære, basert på det vi fant ut i forrige innlegg. Vi kom frem til at vi litt surt og motvillig måtte modellere en atmosfære som består av \(100\%\;CH_4\), som vil være den letteste sammensetningen av atmosfære vi kan få. Det blir kanskje ikke så vanskelig i dette tilfellet, men vi trenger å kjenne til den midlere molekylvekten i atmosfæren vår. La oss ta en kjapp introduksjon:
Midlere molekylvekt
Midlere molekylvekt \(\mu\) er et massemål på massen vi har i atmosfæren vår. Den måles som et slags gjennomsnitt over hydrogenmassen \(m_H = 1.67\cdot10^{-27}kg\). Med andre ord måler vi hvor mye masse vi har av hver gass pr. hydrogenmasse. En litt mer matematisk beskrivelse av det ser slik ut:
\(\begin{align*} \mu = \sum_{i}f_i\frac{m_i}{m_H} \end{align*}\)
der \(f_i\) er prosentvis andel av mengde gass i atmosfære (må variere mellom 0 og 1, og summere til 1) og \(m_i\) er massen til et eller annet gassmolekyl, f.eks \(H_2O\). For å gi deg et eksempel kan vi skrive ned den midlere molekylvekten til en atmosfære som består av \(30\%\;H_2O\), \(30\%\;O_2\), \(20\%\;CH_4\) og \(20\%N_2O\). Da vil midlere molekylvekt se slik ut:
\(\begin{align*} \mu = \sum_{i}f_i\frac{m_i}{m_H} &= 0.3\frac{m_{H_2O}}{m_H} + 0.3\frac{m_{O_2}}{m_H} + 0.2\frac{m_{CH_4}}{m_H} + 0.2\frac{N_2O}{m_H} \\ &= 0.3\frac{2m_H + 16m_H}{m_H} + 0.3\frac{2\cdot16m_H}{m_H} + 0.2\frac{12m_H + 4m_H}{m_H} + 0.2\frac{2\cdot14m_H + 16m_H}{m_H} \\ &= 0.3\cdot18 + 0.3\cdot32 + 0.2\cdot16 + 0.2\cdot44 \\ &= 27 \end{align*}\)
som gir oss en midlere molekylvekt på 27 (antatt da at massen til hydrogen er \(m_H = m_p = m_n\) som er proton og nøytronmassen). Dersom vi gjør dette på vår atmosfære vil vi få at
\(\mu = \frac{m_{CH_4}}{m_H} = \frac{12m_H + 4m_H}{m_H} = 16\)
Dermed vet vi nå at vi har en midlere molekylvekt på 16 for atmosfæren vår, som består av \(100\%\) metangass \(CH_4\).
Antakelser for atmosfæremodellen
Det passer godt nå å introdusere hva slags antakelser og forenklinger vi kommer til å gjøre når vi skal modellere atmosfæren. Det vil være følgende:
- Vi antar at atmosfæren er uniform. I vårt tilfelle ville ikke dette blitt et problem uansett siden gassen allerede er uniform, men dersom vi hadde hatt f.eks \(20\%\) karbondioksid i atmosfæren, hadde det da vært \(20\%\) karbondioksid i hvert eneste punkt i atmosfæren.
- Vi antar også at atmosfæren er sfærisk symmetrisk, som vil si at vi antar at tetthet avtar likt i alle retninger, trykk avtar likt i alle retninger, og temperatur avtar likt i alle retninger radielt ut fra atmosfæren. Med andre ord er tettheten \(\rho = \rho(r)\) der r er avstanden ut til et punkt i radiell retning. Symmetrien impliserer også at det kun er i radiell retning atmosfæren endrer seg, og ikke langs ekvator eller polene.
- Vi antar at atmosfæren er i hydrostatisk likevekt, som betyr at denne likningen her er oppfylt: \(\frac{dP}{dr} = -\rho(r)g(r)\). Dette betyr bare at atmosfæren har stabilisert seg.
- Vi antar at gassen i atmosfæren er en ideell gass, som betyr at denne likningen her er oppfylt: \(P = nkT = \frac{\rho kT}{\mu m_H}\) (ideell gass-lov). Om du ikke husker hva en ideell gass er kan du lese om der her.
- Vi antar at atmosfæren er adiabatisk for høyder til der \(T=\frac{T_0}{2}\), og isoterm etter det. At atmosfæren er adiabatisk betyr det at vi har et forhold mellom trykk og temperatur som sier at \(P^{1-\gamma}T^{\gamma} = konstant\). Der atmosfæren er isoterm betyr det at temperaturen \(T\) konstant er \(T = \frac{T_0}{2}\). Dette er termodynamiske gassegenskaper jeg ikke kommer til å gå noe særlig i dybden på.
- Vi antar at gravitasjonen \(g(r) = g\) i hele atmosfæren. Mens dette kan virke litt bold, så endres faktisk ikke gravitasjonen seg særlig kritisk ut i atmosfæren. Dersom vi regner ut \(g(r) = \frac{GM}{r}\) ved overflaten får vi \(g = 3.17m/s^2\), mens \(100km\) over overflaten gir oss \(g=2.85m/s^2\), som ikke er helt hårreisende. \(100km\) over overflaten på jorda kalles for Kármán-linjen, som kan brukes til å definere linjen mellom atmosfære og det ytre rom (i alle fall på Jorda). Det er derfor ikke en helt dum sammenlikning av gravitasjon ved overflate og 100km over overflaten, og konstant \(g\) eller er heller ikke så dumt i forhold til hvor mye enklere det blir å løse modellen.
Med alle antakelsene i boks er vi klare til å begynne å modellere atmosfæren. Vi har tenkt til å løse dette analytisk, og dette er mye stygg matematikk som jeg ikke kommer til å skrive ned i bloggposten her. Derimot skal jeg linke til en PDF-fil, der de som er interessert i å lese utledningen kan gjøre det. Jeg kan likevel forklare idéen her:
Vi skal bruke antakelsene og forenklingene våre til å få satt opp differensiallikninger, som vi kan løse analytisk. Vi starter med isoterm siden den er enklest, og bruker ideell gass-lov til å finne tettheten og trykket i atmosfæren ved å sette opp en differensiallikning med likningen for hydrostatisk likevekt.
Den adiabatiske delen er litt mer komplisert, men på samme vis. Vi bruker det adiabatiske forholdet mellom temperatur og trykk, ideell gass-lov og likningen for hydrostatisk likevekt, setter opp differensiallikninger, sjonglerer med litt matematikk og finner tettheten, temperaturen og trykket i atmosfæren. Full matematisk utledning kan du finne i linken nedenfor:
Modellere atmosfære - analytisk løsning PDF - nedlastning
Likninger, resultater og plott
Jeg kan gjenta resultatene fra PDF-filen av løsningene på modellen, slik at vi har likningene foran oss:
\(\begin{align*} T_{isoterm} &= \frac{T_0}{2} \\\\ P_{isoterm} &= K_1gC_0e^{-\frac{r}{K_1}} \\\\ \rho_{isoterm} &= C_0e^{-\frac{r}{K1}} \\\\ T_{adiabatisk}(r) &= A^{\frac{1}{\gamma}}\left[\left(\frac{1-\gamma}{\gamma}\right)\cdot(A^{-\frac{1}{\gamma}}K_0gr + C)\right] \\\\ P_{adiabatisk}(r) &= \left[\left(\frac{1-\gamma}{\gamma}\right)\cdot(A^{-\frac{1}{\gamma}}K_0gr + C)\right]^{\frac{\gamma}{\gamma - 1}} \\\\ \rho_{adiabatisk}(r) &= A^{-\frac{1}{\gamma}}\left[\left(\frac{1-\gamma}{\gamma}\right)\cdot(A^{-\frac{1}{\gamma}}K_0gr + C)\right]^{\frac{1}{\gamma - 1}}\cdot K_0 \\\\ A &= T_0\left(\frac{\rho_0}{K_0}\right)^{1-\gamma}\\ C &= T_0A^{-\frac{1}{\gamma}}\left(\frac{\gamma}{1-\gamma}\right) \\ C_0 &= A^{-\frac{1}{\gamma}}\left[\left(\frac{1-\gamma}{\gamma}\right)\cdot(A^{-\frac{1}{\gamma}}K_0g\left(\frac{T_0}{2K_0g}\left(\frac{\gamma}{1-\gamma}\right) - \frac{CA^{\frac{1}{\gamma}}}{K_0g}\right) + C)\right]^{\frac{1}{\gamma - 1}}\cdot K_0 e^{\frac{T_0}{2K_0K_1g}\left(\frac{\gamma}{1-\gamma}\right) - \frac{CA^{\frac{1}{\gamma}}}{K_0K_1g}} \\ &= \rho_{adiabatisk}(r_s)e^{\frac{r_s}{K_1}} \\ r_s &= \frac{T_0}{2K_0g}\left(\frac{\gamma}{1-\gamma}\right) - \frac{CA^{\frac{1}{\gamma}}}{K_0g} \\\\ K_1 &= \frac{kT}{\mu g m_H} \\\\ K_0 &= \frac{\mu m_{H}}{k} \end{align*} \)
Der alle konstanter \(K_0,\;K_1,\;A,\;C,\;C_0\) er kjent fra kjente verdier \(\rho_0,\;T_0,\;\mu,\;m_H,\;k,\;\gamma\). Resultatet vi får dersom vi plotter atmosfæreprofilen vår for de første \(100km\) med verdiene:
| \(\rho_0\) (tetthet ved overflaten) | \(1.048kg\;m^{-3}\) |
| \(T_0\) (temperatur ved overflaten) | \(249.034K\) |
| \(\mu\) (midlere molekylvekt) | \(16.000\) |
| \(m_H\) (hydrogenmasse) | \(1.673\cdot10^{-27}kg\) |
| \(k\) (Boltzmann konstant) | \(1.380 \cdot 10^{-23}m^2kg\;s^{-2}K^{-1}\) |
| \(\gamma\) (adiabatisk konstant) | \(1.400\) |
ser slik ut:
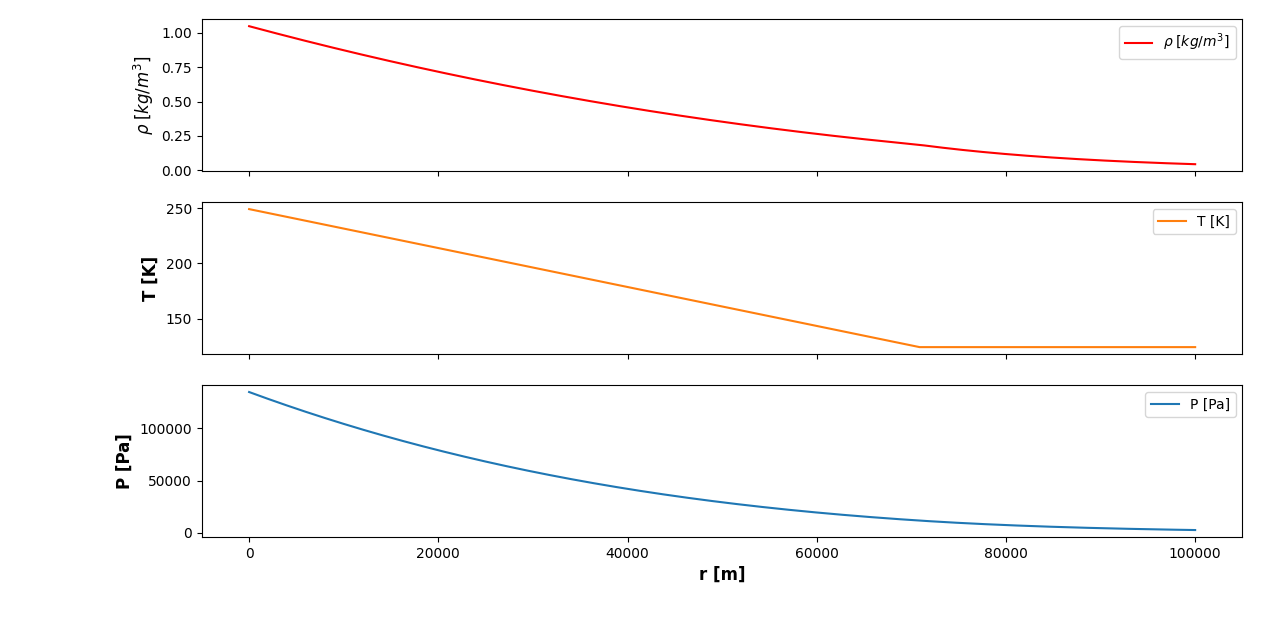
MERK: Det er verdt å nevne for tydelighetens skyld at \(r=0\) her er definert som overflaten til planeten, og ikke sentrum av planeten.
Det første vi merker er at de avtar radielt ut fra overflaten til planeten og ut mot verdensrommet, som lyder veldig bra. Atmosfæren blir jo tynnere og kaldere ut mot verdensrommet. Vi kan tolke fra grafen at på ca. \(70km\) ut på plottet får vi en knekk (mest synlig i temperaturplottet), som er der vi skifter fra adiabatisk atmosfære til isoterm atmosfære. Til sammenlikning kan vi jo se på den tyngste komposisjonen av atmosfære, som ville vært \(100\%\;N_2O\):
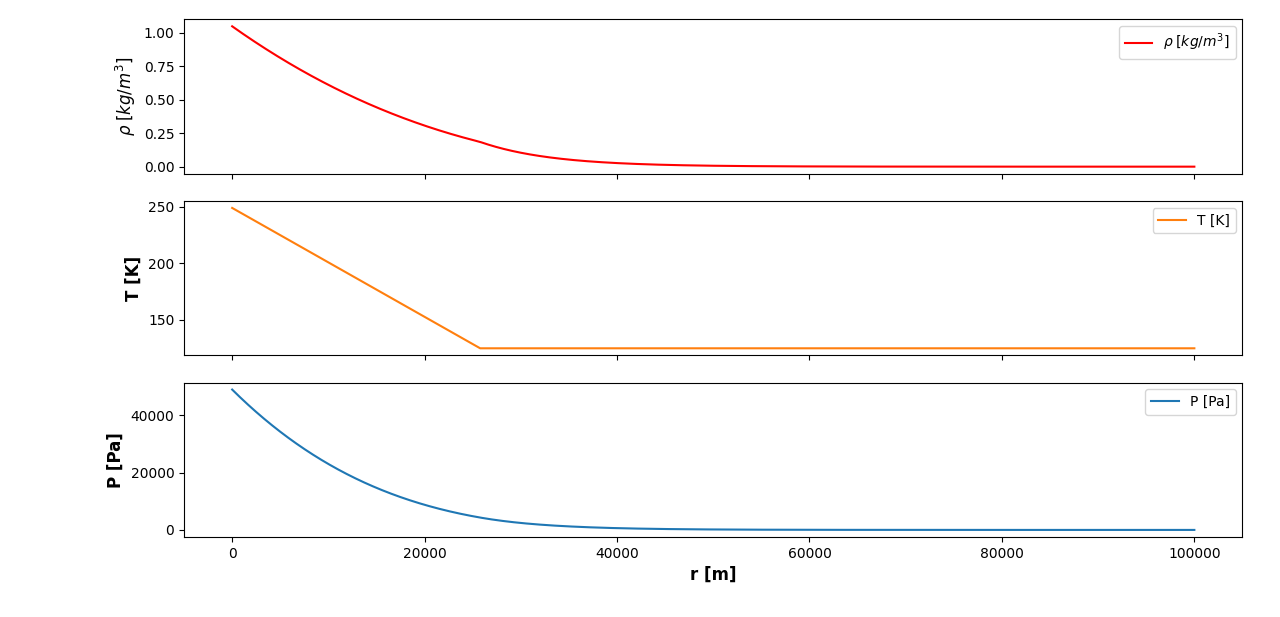
Her skifter atmosfæren mye tidligere mellom adiabatisk atmosfære til isoterm atmosfære (omtrent ved \(25km\)). Det ser ut som at både tetthet, trykk og temperatur er forskjøvet lenger ned mot overflaten, som også er en bra ting for modellen vår siden gassen er tyngre og vil trekkes lenger ned av gravitasjonskreftene fra planeten som fører til høyere tetthet lavere ned mot overflaten. De lettere gassene derimot trekkes ikke like mye av gravitasjonen, og legger seg derfor mer spredt høyere opp i atmosfæren slik som modellen vår viser.
Har antakelsene og forenklingene våre gitt oss en tullete atmosfære?
Resultatene er utledet analytisk, så feilene i svarene våre ligger i alle fall ikke numerisk. Likevel har vi gjort noen antakelser som kan gjøre at atmosfæremodellen vår ikke stemmer helt overens med virkeligheten. Det første jeg kan nevne er temperaturen, som er satt til å være konstant lengst ut i atmosfæren. Dersom vi beveger oss uendelig langt ut vil temperaturen fortsatt være \(T = \frac{T_0}{2}\), som ikke stemmer ute i verdensrommet (som egentlig er lite interessant siden vi modellerer atmosfære og ikke verdensrom). Det er likevel en annen ting vi har gjort som forenklet løsningen vår, men som også har forfeilet den. Antakelsen om konstant gravitasjonsakselerasjon vil ha en påvirkning på resultatet vi har fått. Slik som vi oppdaget tidligere har vi en \(g = 3.17m/s^2\) nede på overflaten ved \(r=0\), og \(g=2.85m/s^2\) i atmosfæren ved \(100km\). For å gjøre et ekstra mål kan vi sjekke ved ISS-høyde som er ca. \(410km\) opp i atmosfæren, og vi får at \(g = 2.13m/s^2\). Som jeg nevnte tidligere er det ikke helt katastrofalt å anta konstant gravitasjon, men definitivt noe som vil påvirke nøyaktigheten på modellen opp mot virkeligheten. Jo lenger ut i atmosfæren vi beveger oss, jo mer feil blir denne antakelsen, så den passer best for lavere høyder i atmosfæren, men gir oss en grei modell vi kan bruke. Dermed er vi ferdige med å bygge atmosfæremodellen, og vi bruker det vi nå har klart å finne til å simulere landinger for å se om det finnes noe håp for oss om å overleve en landing på denne underlige verdenen. Chiao, ses i neste innlegg!