Oppskytning - opptak 2
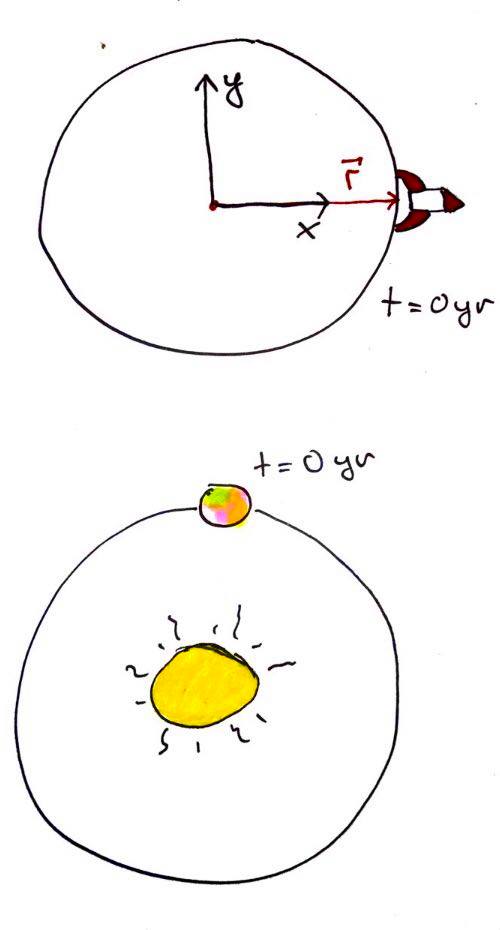
MERK: på toppen er raketten plassert på overflaten til planeten, ikke på planetbanen slik som illustrasjonen under.
Ålreit, jeg skal ikke lyve for dere: å skyte opp raketter er vanskelig. Det krever mye av oss mennesker, og vi må være smartere. Tidligere under testoppskytning i innlegget We have liftoff ... or? begrenset vi oss til å skyte opp fra et spesifikt sted på planeten, et spesifikt sted i planetens bane (ved initialposisjonen t=0, se figur 1). Om vi skal låse oss til dette kan det blir veldig vanskelig for oss å komme frem til destinasjonen vi ønsker, og dermed ønsker vi mer frihet til å kunne skyte opp hvor vi vil på planeten, i et hvilket som helst tidspunkt i planetbanen til hjemplaneten vår. Vi trenger en løsning på dette!
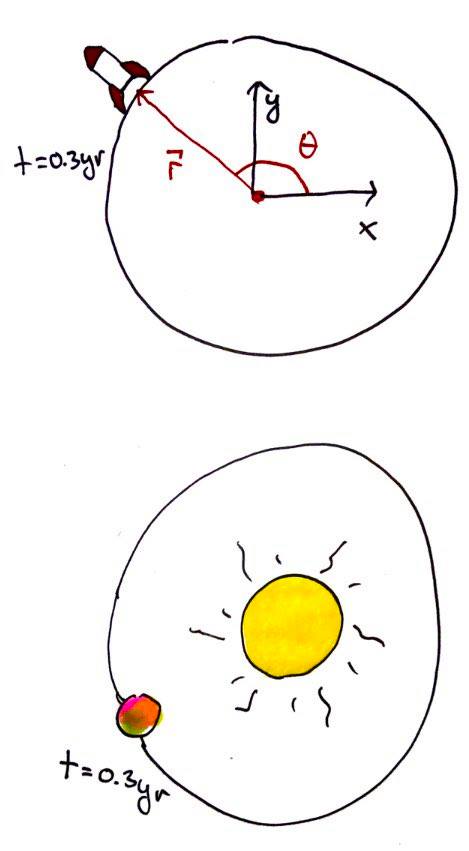
Det første vi kan gjøre er å innføre en ny parameter \(\theta\) som skal beskrive vinkelen mellom posisjonsvektoren \(\vec{r}\) til raketten fra sentrum av planeten, og x-aksen i koordinatsystemet definert med origo i sentrum av planeten (se figur 1 og figur 2). Dette blir da vinkelen vi bruker til å rotere posisjonen til raketten på planeten, og det blir også vinkelen vi bruker når vi setter initialhastigheten til raketten (slapp av, jeg skal forklare det mer senere). Vi innfører også en ny parameter \(t\), som skal angi tidspunktet for planetens bane om stjerna i år. Da trenger vi å hente inn dataen vi regnet ut for planetbanene i innlegget Solsystemet på dataform, slik at vi kan vite hvor i solsystemet vi befinner oss etter å ha skutt opp raketten. Metoden vi kommer til å bruke begynner vel å bli velkjent, numerisk integrasjon for å finne rakettens posisjon og hastighet. Likt som i innleggene Solsystemet på dataform og Sol-dans og planet-vals kommer vi til å bruke leapfrog til å integrere hastighet og posisjon numerisk i koordinatsystemet med planetens sentrum i origo, så om du ikke har husker eller vet hva det er anbefaler jeg å ta en titt på det, fordi det går jeg ikke gjennom her! Verdiene jeg så returnerer er transformert til koordinatsystemet med stjernas sentrum i origo, slik at vi kjenner til rakettens posisjon i forhold til stjerna. Vi kan jo ta en liten oppsummering / punktvis gjennomgang på hvordan vi går frem for å løse problemet:
- Vi innfører to nye parametere \(\theta \) og \(t\) som skal hjelpe oss med å beskrive rakettens posisjon på planeten og initialhastigheten raketten får fra planetens rotasjon (\(\theta\)), og tidsunktet vi skyter opp raketten i planetens bane (\(t\)) slik at vi har frihet til å skyte oss ut hvor vi vil.
- Vi finner uttrykket for akselerasjonen til raketten ved hjelp av Newtons 2. lov, og bruker leapfrog til å integrere opp posisjon og hastighet numerisk.
- Til slutt transformerer vi posisjonen og hastigheten vi har funnet fra koordinatsystemet med planetens sentrum i origo til koordinatsystemet med stjernas sentrum i origo. Der vi integrerer numerisk bruker vi SI-enheter, mens dataen til planetens posisjon og hastighet er gitt i astronomiske enheter, så det er viktig å være obs på det.
Litt mer detaljert takk ...
Vi kan starte med å representere tall og symboler vi bruker i utregningene her:
| Symbol | Verdi | |
|---|---|---|
| Rotasjonstid om egen akse | \(T\) | 98502s (ca. 1.14 dager) |
| Radius på planet | \(r_p\) | 7605752m (7605.752km) |
| Total masse på rakett | \(m_r\) | 1100kg (rakett) + 4000kg (drivstoff) |
| Masse på planet | \(m_p\) | \(8.54\cdot 10^{24}\)kg |
| Thrust-kraft til raketten | \(\vec{F}_r\) | \(4.4\cdot10^4\frac{\vec{r}}{|\vec{r}|}N\) |
Vi starter med første punkt på linjen over: hvordan kan vi bruke parameterene \(\theta\) og \(t\) til å beskrive bestemme hvor vi skal skyte oss ut? La oss ta en kjapp titt på \(\theta\), også kommer vi tilbake til parameteren \(t\) etterpå. Vi ønsker å kunne skyte oss opp hvor som helst langs ekvator på planeten vår. Det er viktig å spesifisere det når jeg sier skyte opp hvor som helst på planeten, da er det altså ment som på ekvator. Kjapp kommentar på det er fordi der kan vi bruke radiusen til planeten, og det er der vi får mest fart fra planetens rotasjon. Tilbake til posisjonen: Du er kanskje kjent med hvordan vi parameteriserer en sirkel? En sirkel er parameterisert som \(\vec{r} = (r\cdot cos(\theta), r\cdot sin(\theta))\) der \(r\) er radiusen til sirkelen, og \(\theta \) er vinkelen mellom x-aksen og posisjonsvektoren \(\vec{r}\) med lengde \(r\) langs banen. Det er lett å tenke på det dersom du tenker på enhetssirkelen, som jeg håper du er kjent med. Vi bruker denne parameteriseringen til å beskrive posisjonen vår langs ekvator på planeten vår, og uttrykket for initialposisjonen vår blir da
\(\vec{r}=(r_p\cdot cos(\theta), r_p\cdot sin(\theta)) = r_p\cdot(cos(\theta), sin(\theta))\)
der \(\theta\) ligger mellom \(0 \) og \(2\pi\).
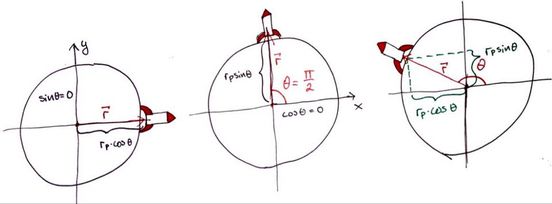
Vi kan også bruke denne vinkelen til å finne initialhastigheten vår. Siden planeten roterer om sin egen akse, antar vi at den roterer med konstant hastighet og kan finne uttrykket for farten vi har på overflaten:
\(v_0=\frac{2\pi r_p}{T}\)
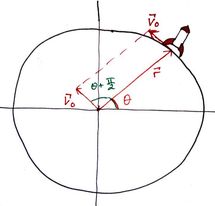
der \(r_p\) er planetens radius, og \(T \) er tiden den bruker for en rotasjon om egen akse. Dette er farten vi har tangensielt på planetens overflate, som vil si at dette er fart vi får med oss når raketten skyter opp. Men vi trenger også retningen til farten, ikke bare størrelsen. Hvordan vet vi hva den er? Det er kanskje ikke veldig vanskelig å overbevise deg om at denne farten har en retning som er vinkelrett på posisjonsvektoren? Siden det er en sirkelbane, så må hastigheten være tangent på sirkelkurven. Men hva er det matematiske uttrykket for det? Vel, siden vi nå antar at planeten roterer mot klokka kan vi tenke oss at vi vil ta enhetsvektoren som peker med posisjonsvektoren \(\vec{r}\), rotere den \(90^o\) mot klokka, og skalere den med farten \(v_0\) som vi akkurat fant. Vi vet at enhetsvektoren som går langs med \(\vec{r}\) kan skrives som
\(\hat{r} = (cos(\theta), sin(\theta))\)
Siden vi ønsker å rotere denne \(90^o\), eller \(\frac{\pi}{2}\) radianer, kan vi legge til \(\frac{\pi}{2}\) på \(\theta\), og få enhetsvektoren langs hastigheten på overflaten til planeten, \(\hat{v}\). Vi bruker to trigonometriske identiteter, og ender opp med
\(cos(\theta + \frac{\pi}{2}) = cos(\theta)cos(\frac{\pi}{2}) - sin(\theta)sin(\frac{\pi}{2}) = -sin(\theta)\)
\(sin(\theta + \frac{\pi}{2}) = sin(\theta)cos(\frac{\pi}{2}) + sin(\frac{\pi}{2})cos(\theta) = cos(\theta)\)
og dermed
\(\hat{v} = (-sin(\theta), cos(\theta))\) og \(\vec{v}_0 = v_0\hat{v} = v_0(-sin(\theta), cos(\theta))\).
Så langt har vi funnet ut hvordan vi kan endre posisjonen vår på planeten, og hvordan vi uttrykker initialposisjon og initialhastighet til raketten sett fra koordinatsystemet med planetens sentrum i origo ved hjelp av parameteren \(\theta\).
Det neste vi trenger nå er å finne akselerasjonen til raketten sett fra planeten. Kreftene som virker på raketten er kraften fra rakettmotoren, og gravitasjonskraften. Vi setter opp N2L og har uttrykket
\(\sum\vec{F} = m_r\vec{a} = \vec{F}_r + \vec{F}_g = 4.4\cdot10^4\frac{\vec{r}}{|\vec{r}|}- G\frac{m_pm_r}{|\vec{r}|^2}\frac{\vec{r}}{|\vec{r}|}\)
der \(\vec{F}_r\) er thrust-force fra rakettmotoren og \(\vec{F}_g\) er gravitasjonskraften. Deler vi på \(m_r\) på begge sider får vi at akselerasjonen til raketten er
\(\vec{a} = \frac{4.4\cdot10^4}{m_r}\frac{\vec{r}}{|\vec{r}|}- G\frac{m_p}{|\vec{r}|^2}\frac{\vec{r}}{|\vec{r}|}\)

OBS OBS OBS! Her skal vi passe oss! Det vi må huske på her er at massen \(m_r\) blir mindre og mindre over tid, fordi raketten forbrenner drivstoff og mister masse over tid. Det betyr at massen \(m_r=m_r(t)\) er en funksjon av tid. Heldigvis blir ikke det store problemet for oss som gjør det numerisk, siden vi har data på hvor mye masse i kg vi mister pr. sekund. Alle detaljer om raketten kan du finne på innleggene Rakettmotor - boks for boks og We have liftoff ... or?. Det betyr bare at for hver gang vi itererer i integrasjonsløkka med leapfrog er vi nødt til å oppdatere hva den totale massen er, og så oppdatere uttrykket for akselerasjonen med en nye totale massen. Det kan vi finne ved å trekke fra
\(\text{total mass} = \text{total mass} - \text{mass consumed pr. sec}\cdot\Delta t \)
for hver gang vi itererer i integrasjonsløkka, og bruke den nye totale massen i uttrykket for akselerasjon over. Vi bruker denne informasjonen vi har kommet frem til, og kaster det inn i leapfrog. Det spyttes ut et resultat, men det kan vi ikke bruke. Vi ønsker å se det i koordinatsystemet til stjerna, ikke planeten. Vi må gjøre en liten transformasjon, og om du ikke husker alt om å bytte fra et koordinatsystem til et annet er det beskrevet i bloggposten Sol-dans og planet-vals. Denne gangen er det litt enklere, og alt vi trenger å gjøre er å legge til planetens posisjon og hastighet i tidspunktet vi velger å skyte opp raketten. Det er her dataen fra planetbanene i Solsystemet på dataform og parameteren \(t\) kommer inn! Her må vi være forsiktige, for nå har vi noe data som er i SI-enheter, og andre i astronomiske enheter. Vi må passe på å gjøre om dataen i SI-enheter over til astronomiske enheter. Vi har at
\(1 AU=149 597 870 700 m \Rightarrow 1m = \frac{1}{149 597 870 700}AU\approx 6.6\cdot10^{-12}AU\)
\(1yr = 31536000s \Rightarrow 1s = \frac{1}{31536000}yr\approx3.2\cdot10^{-8}yr\)
. Vi velger oss et tidspunkt \(t\), og den endelige transformasjonen blir
\(\vec{R} = \vec{r}\cdot6.6\cdot10^{-12}AU + \vec{r}_p(t)\)
\(\vec{V} = \vec{v}\cdot\frac{6.6\cdot10^{-12}AU}{3.2\cdot10^{-8}yr} + \vec{v}_p(t)\)
Dermed er vi klare for å teste oppskytning, og til å se hvordan det går!
Resultat av oppskytning
Steike! Dette gikk visst dårlig denne gangen også, som i aller første oppskytning på We have liftoff ... or?. Det er ikke helt sikkert hva som går galt, men vi treffer fortsatt ikke der vi skal. Det er mulig vi har misforstått et konsept, gjort en regnefeil i programmet eller rett og slett implementert det feil. Samme metode vi har brukt her har funket fint tidligere som ved beregning av planetbaner eller løsningen av to-legeme problemet, så jeg setter liten tvil på at det er metoden vår det er noe galt med.. Vi tar kontakt med NASA og får hjelp fra noen av deres fremste eksperter, som skriver et program for oss som sender oss på riktig sted. Aureka! Disse forskerene fra NASA er brilliante! Koden deres kjører feilfritt og vi får en suksessfull oppskytning! Noe vi kjenner en ergelig sjalusi over.. men det må vi bare riste av oss, svelge den harde klumpete stoltheten, og komme oss videre til neste del.